こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
最近以下のツイート内容について考えています。
断熱真空膨張の場合外部への仕事を0とみなして内部エネルギーが変わらない。理想気体を仮定すると内部エネルギーは温度のみに依存するため膨張後も温度は変わらない(ゲイリュサック・ジュールの実験)
位置エネルギーがある場合は、内部エネルギーが上昇して理想気体を仮定する気体の温度は上がる? pic.twitter.com/ksTW2zBvdC— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) April 25, 2021
簡単にまとめると「位置エネルギーを利用すると気体の体積膨張によって温度は上がるのか?」という疑問です。
熱力学に多少触れたことがある人であれば気体の体積が膨張すると温度が下がるという認識を持っている人が多いと思います。
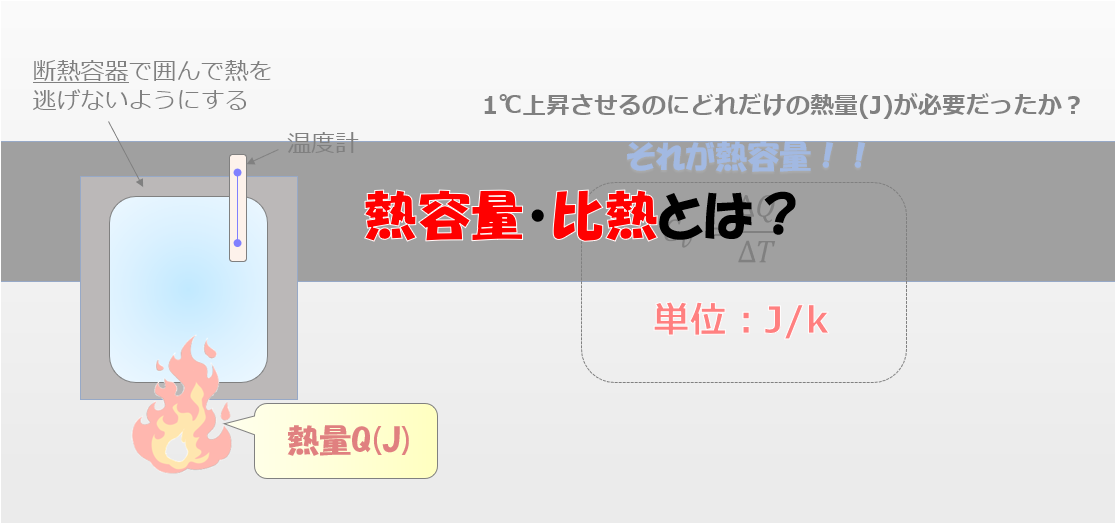
容器にnモルの気体を入れて出入りできなくします。
その状態で容器の容量を増やします。
平衡状態になるまでしばらく待ちます。
どうなると直感的に思いますか?
※理想気体と仮定状況設定をあまり伝えず・・
直感的にはどう思うものなのかな?(・o・)— カマキリ🐲@物理ブログ(宇宙に入ったカマキリ) (@t_kun_kamakiri) 2019年5月30日
少々いじわるな質問だと思っています。もう少し詳細な状況設定を考えないと何とも言えないというのが正確な回答ではないかと思います。
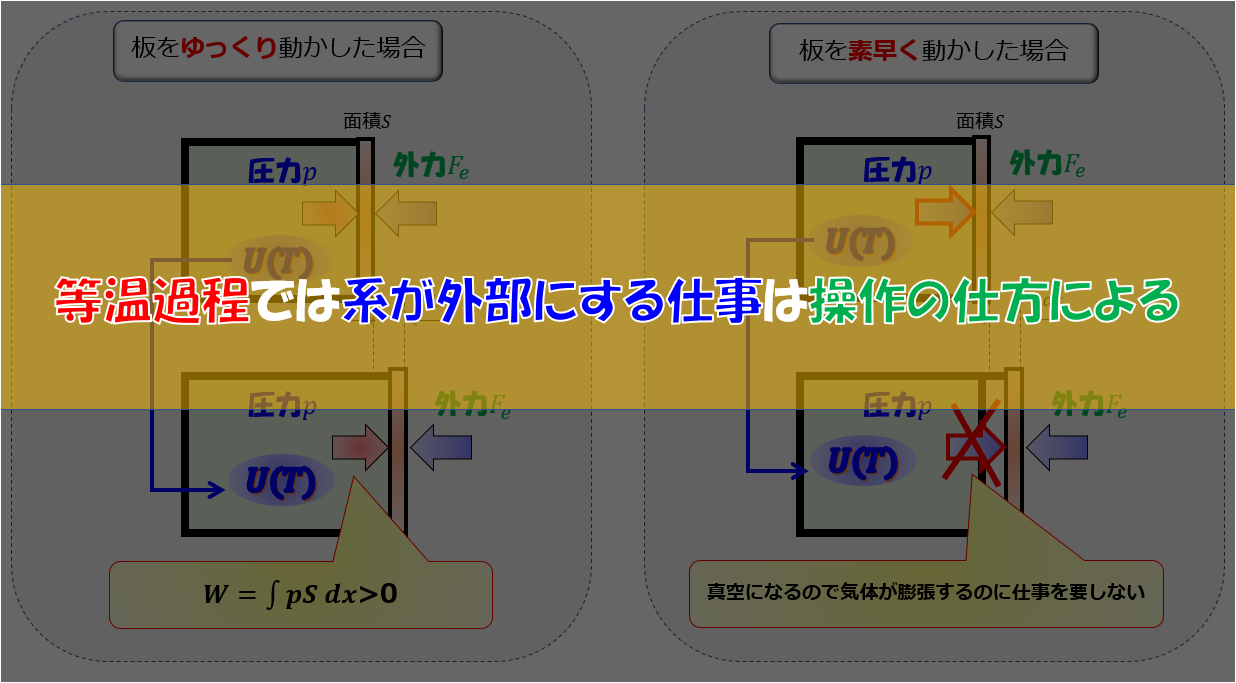
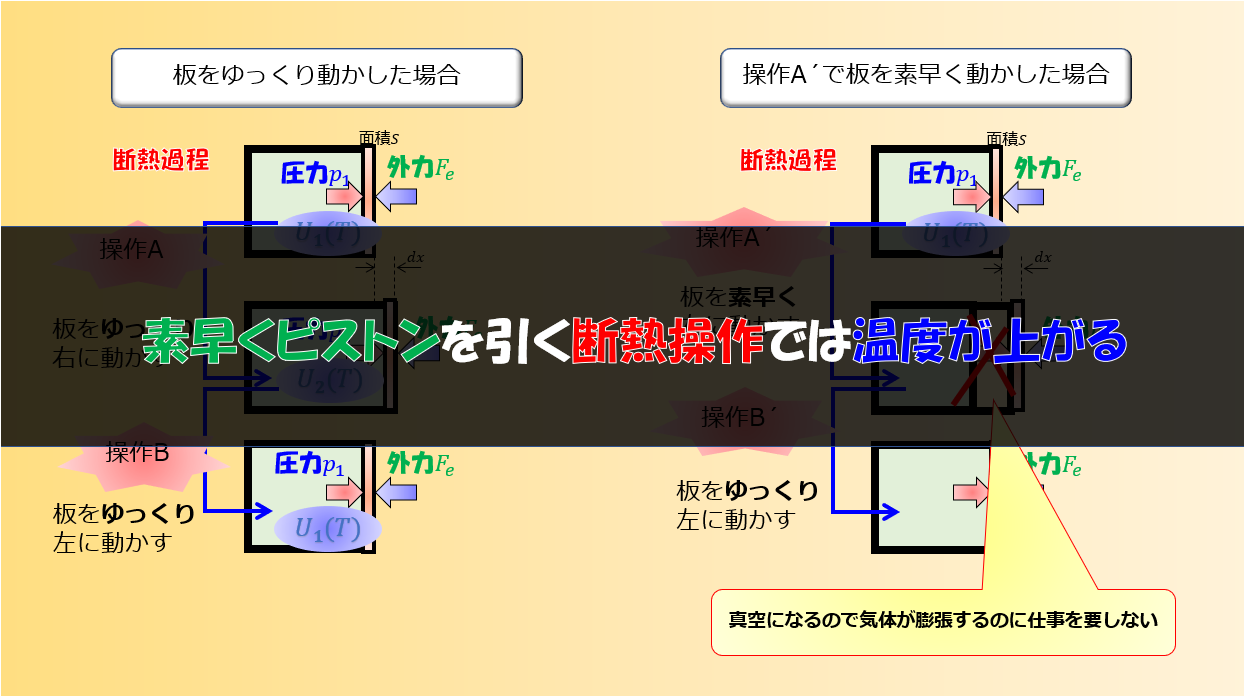
過去の記事でも書きましたが、気体の体積膨張によって温度が下がる過程は断熱過程においてです。体積変化しても温度が変わらない過程や温度が上昇する過程も考えることができます。
そういった事例は過去の記事でも解説を行いましたのでご参考ください。
今回は、
気体の体積膨張によって温度が上がる過程があるのか?
ということについて考えたいと思います。
理想気体の要請
理想気体とは、以下の条件でも実現象を再現しうるのに適した簡単なモデルだと考えられています。
- 気体の分子間力は考慮しない
- 気体の大きさを考慮しない
熱力学的には分子の運動エネルギーが内部エネルギーに相当するエネルギーであり、分子間の相互作用もエネルギーとして考えなければなりません。しかし、ここでの「気体の分子間力を考慮しない」というのは、分子の運動エネルギーが分子間相互作用よりも大きい高温状態で良い近似となります。
さらに気体分子の大きさ$a$と比較して考えている系の体積$V$が十分大きいため、$a^3<<V$の状態である場合は、気体の大きさを考慮しないで十分問題を考えることができます。
それによって、理想気体の状態方程式$pV=nRT$が気体において良いモデルとなります。
あともう一つ理想気体における重要な要請を書いておきましょう。
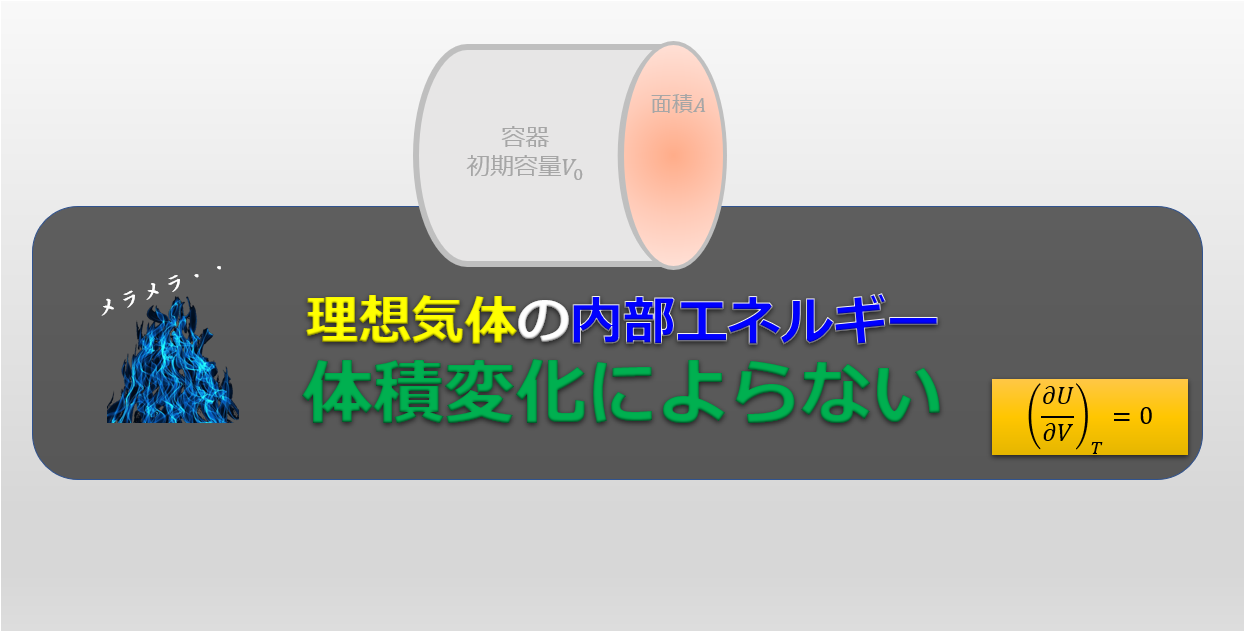
理想気体の内部エネルギー$U(T,V)$は$\big(\frac{\partial U}{\partial V}\big)_{T}=0$となり、理想気体の内部エネルギーは体積に依存せず、温度のみに依存する。
内部エネルギーは定積比熱$C_{V}$を使って$U(T)=nC_{V}T$と簡単に書けます。
定積比熱は温度依存性があって本当は$C_{V}(T)$と書いておく方が良いというのは、こっそりと述べておこうと思います。
とにかく理想気体をにおいては内部エネルギーは温度の増加関数であるということです。
\bigg(\frac{\partial U}{\partial V}\bigg)_{T}=0\tag{1}
\end{align*}
内部エネルギーは温度のみに依存し、ここでは詳しく述べないですが温度の増加関数であります。つまり、温度がどうなるのかというのは、内部エネルギーの変化を考えることで必然的に決まるということです。
理想気体は実在しない簡素化したモデルですが、気体の多くは常温で理想気体として扱っても問題ありません。
熱力学第一法則の使い方
熱力学第一法則は以下のように書かれます。
後で説明しますが、(2)のように書くとき$d^{‘}W$の意味は気体が外へする仕事という意味です。
熱力学第一法則を言葉書くと、
「外部から与えられた熱量」=「内部エネルギー」+「外へする仕事」
外部から与えられた熱量
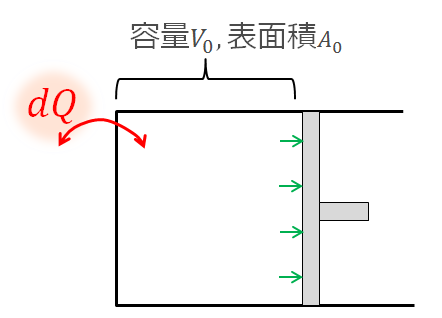

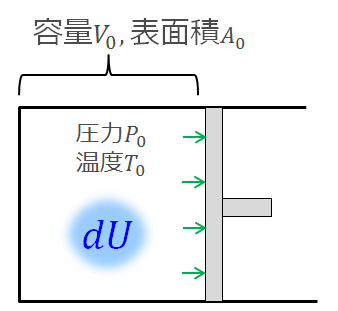
この熱量を使って内部に溜まるエネルギー(内部エネルギー)
内部エネルギーは気体の状態(圧力、温度)に関係するエネルギーのことです。

それから体積膨張するために外へする仕事
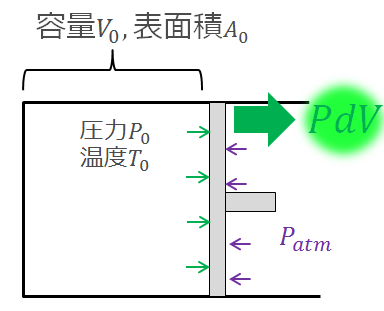

まとめると以下のように書くことができます。



このよう理解することができ、とてもシンプルな式ですが正直どのように使ったら良いのかわからないというところでしょう。
熱力学第一法則はしばしば以下のように書かれます。
よく見ると(1)の場合と$d^{\prime}W$の符号が逆になっていますね。
これは、外から仕事をした分内部エネルギーとして気体にエネルギーを蓄えますよという式の見方です。



| A:ポイントその1 | B:ポイントその2 |
| 熱力学第一法則 | 状態量と状態量でないものを区別する書き方 |
| 熱量=内部エネルギー+気体(系)がする仕事量 | \(Q=\Delta U+W\) ※\(\Delta U\)は状態量 ※\(W\)は気体がする仕事量 |
| 内部エネルギー=熱量+外部が(系に)する仕事 | \(\Delta U=Q +W_{e}\) ※\(\Delta U\)は状態量 ※\(W_{e}\)は外部が系にする仕事量 |
(2)のように書くことで人が手を加えてした仕事が直接気体の状態を変えるエネルギーに変えるという見方ができるようになります。
しかし、仕事を気体にしたはずがイコールとはなりません。
つまり、本来気体の内部エネルギーによって外へする仕事に変換されるのですが、どうも辻妻が合わない・・・・その辻褄が合わないエネルギー量を熱量として加えることで熱力学第一法則としています。
【熱力学第一法則の使い方】
U=Wで辻褄が合わなかった分を全部Qにぶちこむ。
対流熱伝達、熱伝導、気化熱、ガス膨張など全部。— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) November 2, 2021
熱量の外部からの熱量に限ったことではなく、外からする仕事(もしくは気体が外へする仕事)と内部エネルギー以外のエネルギー量の全てを指しています。
単位時間あたりに吸収・放出する熱量には以下のものがあります。
- 熱伝導:$\lambda \frac{T-T_{out}}{l}$
- 熱伝達:$-hA(T-T_{out})$
※輻射熱の式は状況によるため省略 - ガス流出:$m C_{p} T$(定圧比熱$C_{p}$[J/kg K]定圧過程で断熱膨張するとする)
- 気化熱(状態変化による潜熱$C_{Ev}$[J/kg]):$mC_{Ev}$
ここに位置エネルギーも加えておきましょう。
- 位置エネルギー$E_{pot}=mgh$
※正確には高さによって密度が不均一なので$U=\int \rho(z)gAdz$のように積分する必要がありますが、ここでは密度の不均一さが目立たないような系を考えているとしましょう。
体積膨張による温度上昇
(1)初期状態
初期状態として断熱材に囲まれた容器の上側半分を気体を詰め、下半分は真空にしておきます。気体と真空部分は仕切りをして混ざらないようにします。
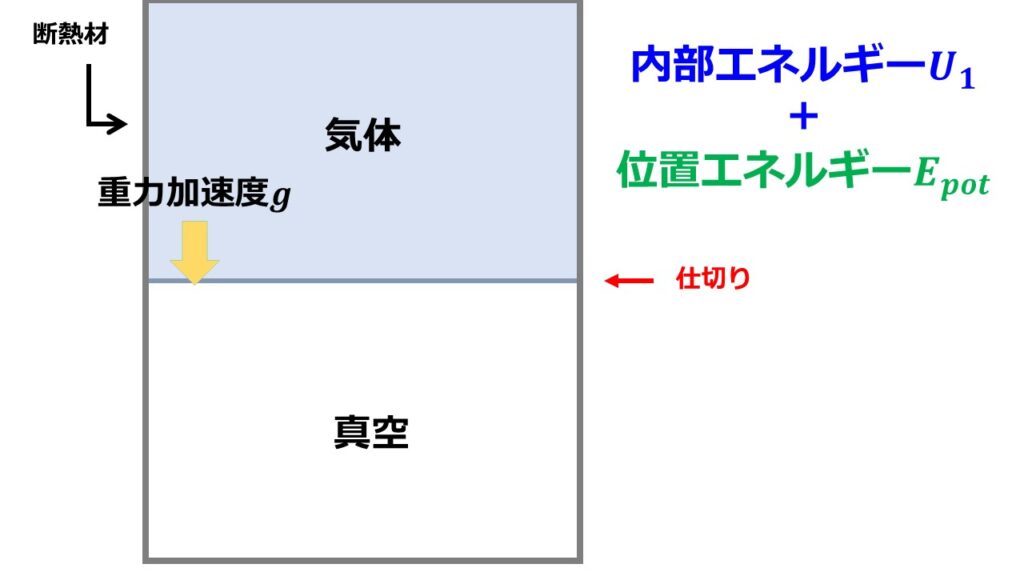

(2)仕切りを系に影響を与えないように取り外します。
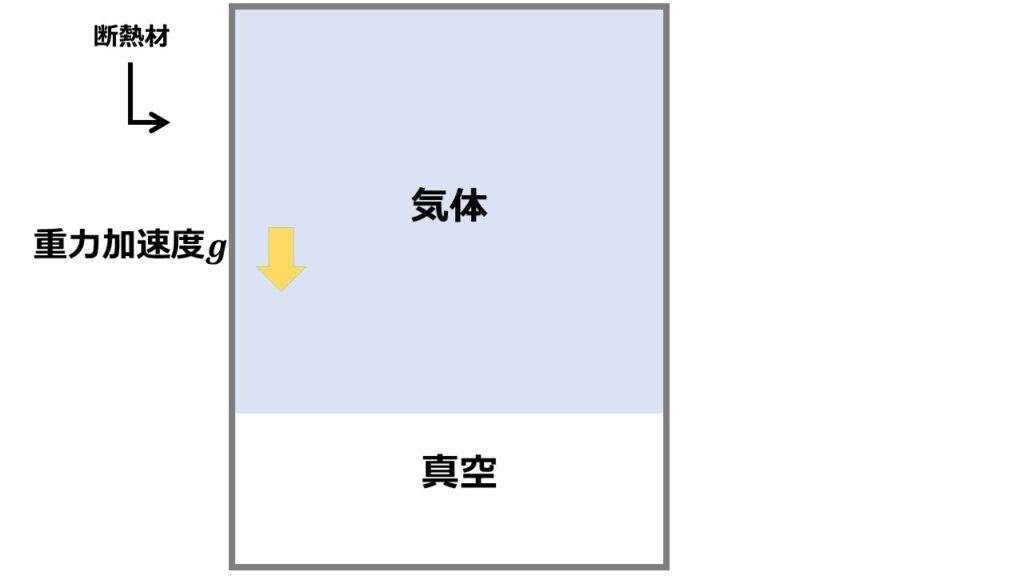

気体は体積膨張をして真空部分に侵入することでしょう。
ここで体積膨張しているということに注目しましょう。しかし、気体の体積膨張に関しては気体がする仕事量$d^{\prime}W=0$です。
なぜなら真空なので仕事を必要とせず自由膨張するからです。
(3)最終状態


※断熱材で囲んでいるため内部エネルギー・位置エネルギー以外に考えるエネルギーはありません。
内部エネルギーは状態量なので初期の気体の内部エネルギーを$U_{1}$とし、最終状態の内部エネルギーを$U_{2}$とします。
この過程においてエネルギー保存則より、
となります。
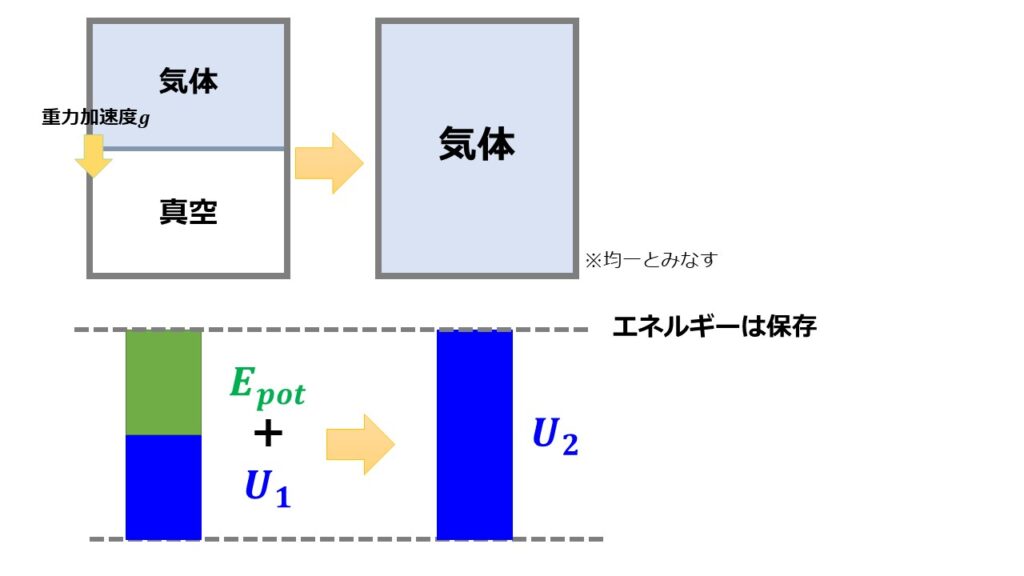


$E_{pot}>0$であるため$U_{2}>U_{1}$となり初期状態より最終状態の方が内部エネルギーが大きいということになります。
ここで、「理想気体の内部エネルギー$U(T,V)$は$\big(\frac{\partial U}{\partial V}\big)_{T}=0$となり、理想気体の内部エネルギーは体積に依存せず、温度のみに依存する」といことを思い出すと、位置エネルギーを利用することにより初期状態より最終状態の方が温度が高いということになります。
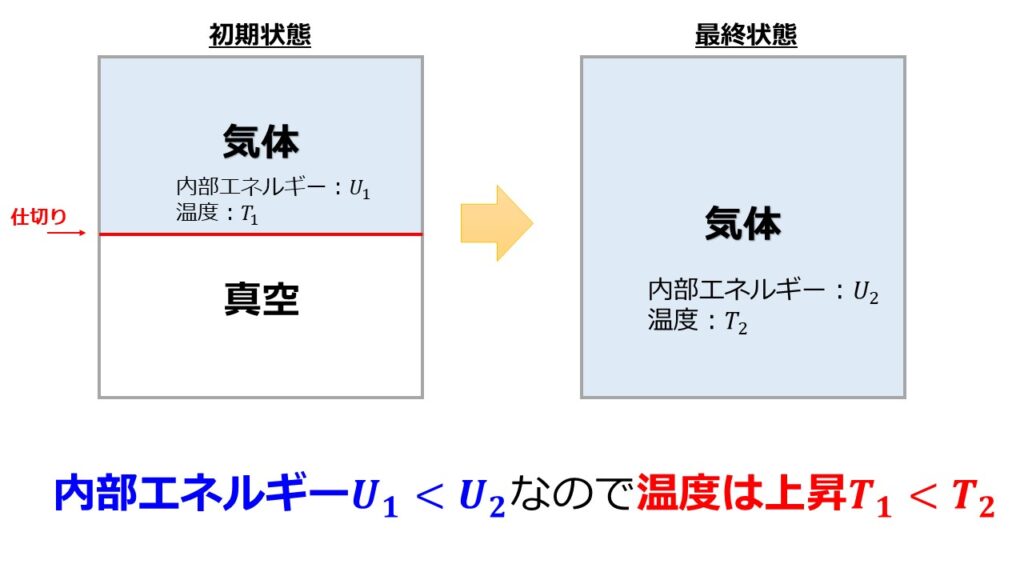

体積膨張する過程により最終状態の温度が上がる過程があるという結論です。
位置エネルギーによりどれだけ温度上昇するか
ではどれくらい位置エネルギーを利用すると温度が上昇するのか計算をしてみましょう。
計算方法はとても簡単です。
内部エネルギーが$U=mC_{V}T$と書けるためエネルギー保存則より
よって、
となります。
温度上昇分は$\frac{gz}{C_{V}T_{1}}$ということになりますね。
これがどれだけ温度上昇に寄与しているのかを概算で出してみましょう。
今回気体は空気であると考えます。
質量:$m=1$kg
定積比熱:$C_{V}=1000]$[J/kg K]
※だいたい定圧比熱$C_{p}$が既知であることが多いですが、定積比熱は比熱比$\gamma = \frac{C_{p}}{C_{V}}=1.4$くらいなので概算で定積比熱は出せますね。
初期状態の温度が$T_{1}=20$[℃]$=293$[K]とします。
$C_{V}T_{1}=2.93\times 10^{5}$[J/kg]となりました。
重力加速度$g=9.8$[m/$s^2$]であることを考えると、位置エネルギーの高さは$30000$[m]でようやく1℃温度上昇するくらいです・・・・
もう少し比熱の小さな気体であるアルゴンは空気の約半分($C_{V}=500$[J/kg K]程度)ですがそれでも位置エネルギーを使って温度上昇は現実的な高さではなさそうです。
まとめ
上半分に気体を入れ位置エネルギーを利用することで最終状態の温度が高くなる過程を考えました。



お勧めの熱力学の参考書
お勧めの熱力学の参考書は以下の記事で紹介しています。
記事を読むが面倒な方はとりあえず以下の参考書を手元に置いて置けばよいでしょう。(積読せず)
ここに本文を入力