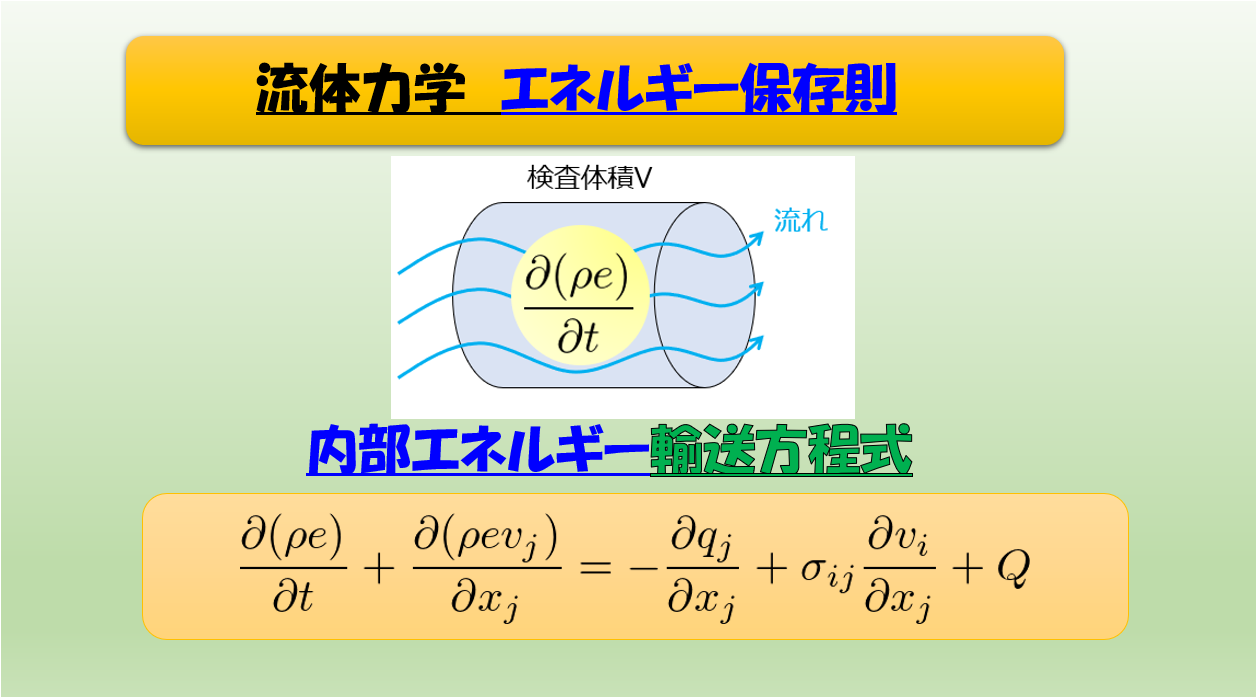
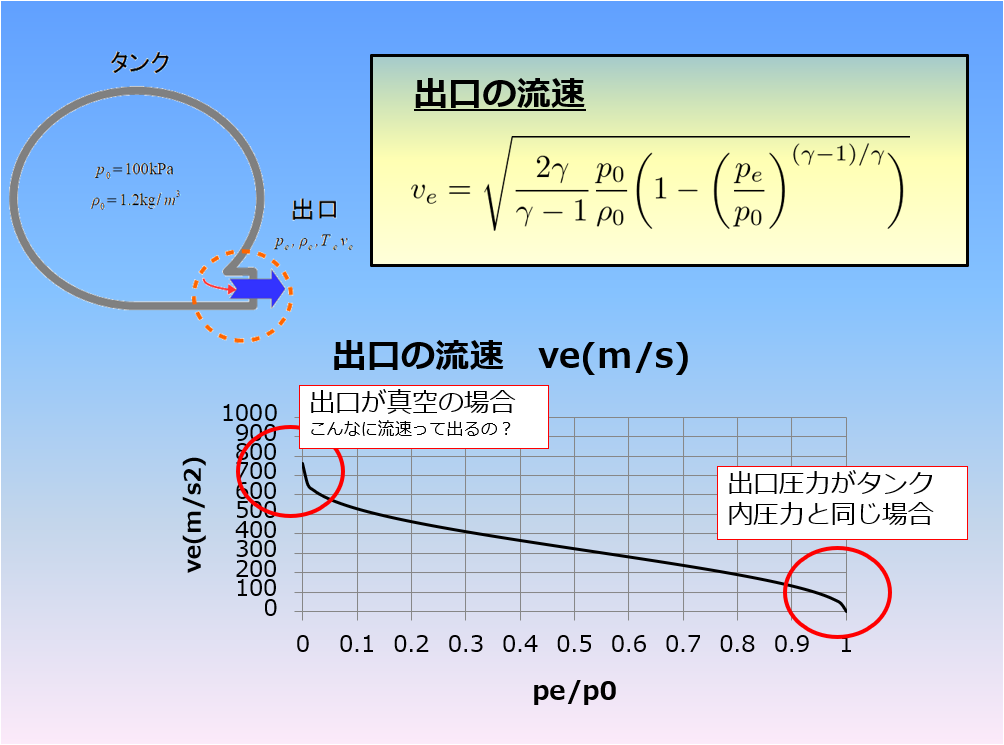
さてクヌッセン数とはなんでしょうか?
実は流体力学のほとんどの教科書のはじめにクヌッセン数(クヌーセン数)の記述があります。
しかし、流体力学を深く学んでいくと全然意識されなくなるのがこのクヌッセン数です。
なぜこのような量を考えるのかというと、流体力学が連続体近似だからです。
つまり、クヌッセン数という量を持ち出して、「流体力学はこのような仮定のもと成り立っているんですよ」ということをはじめに明記しておく必要があるので、ほとんどの教科書のはじめにクヌッセン数の説明があるのです。
流体現象を数学的に扱う際にまず、連続体がどういう考え方のもとになっているのかを学ばなければなりません。
連続体とは
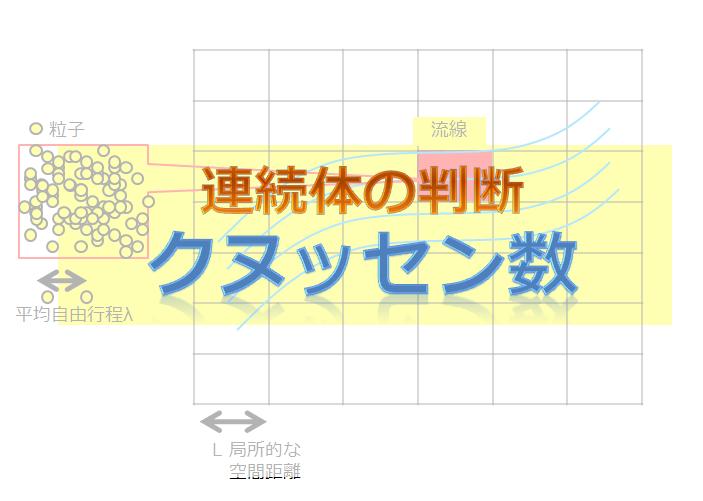
よく見かけるような川の流れのようなものを考えます。
例えば、下記のような流線を描くことにします。
こういった流れをどうやって数学的に扱のでしょうか?
まさか、「流体現象を原子レベルで考えてそこから考える」なんてことはしないはずです。しても良いでしょうがとんでもない量の個々の粒子の運動方程式を解いても実りある結果がでるとは思いません。(解けるのかという問題と、解いた後どう解釈すれば良いのかという2つの問題があります。)
むしろ流体現象は大多数の粒子の集団として平均的な物理量をもって運動しているのだという立場にたって考えた方が良いでしょう。
これは熱力学でも統計力学でも考え方は同じです。
つまり、「大多数の粒子が存在しているから、その粒子間の相互作用などが影響し合って統計的にある平均的な物理量に落ち着く」という考え方を取るのです。
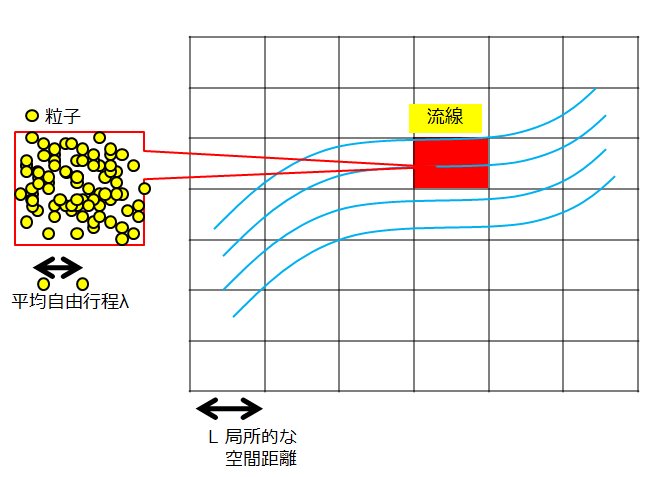
このように局所空間内(個々のセル内)ではとてつもない粒子がうじゃうじゃ動いているのですが、その詳細の運動には興味がなく、「むしろ個々の粒子集団を平均化した赤色の空間の物理量」に興味があるのです。
赤色の局所空間の座標を\(x\)とおくとき、そのときの平均的な値である物理量(マクロな物理量)には、速度\(v(x)\)、圧力\(p(x)\)、温度\(T(x)\)、密度\(\rho (x)\)などが定義されます。
このマクロな物理量はセル内で関数として定義され、それが隣のセルと連続的な値を持っている構造をとなっています。
これが連続体ということになります。
クヌッセン数
では、連続体かどうかを判断する指標というものを考えないといけません。
連続体というからには、「大多数の粒子がセル内に存在する」という仮定があります。
この仮定を表現する指標となるのがクヌッセン数です。
クヌッセン数とは、下記のように定義されています。
クヌッセン数は次の式で定義されます:
ここで
$\lambda$:平均自由行程 (m)
$L$ :代表長さ (m)
$T$ :温度 (K)
$k_B$ : ボルツマン定数 (J/K)
$P$ :全圧 (Pa)
$\sigma$:分子直径 (m)
もっとわかりやすく言うとですね・・・・・
個々のセルの大きさ\(L\)は、平均的に動ける個々の粒子の平均値(これを平均自由行程\(\lambda\)よりも十分に大きければ連続体と見なすってことです。
この考え方はとても重要です。
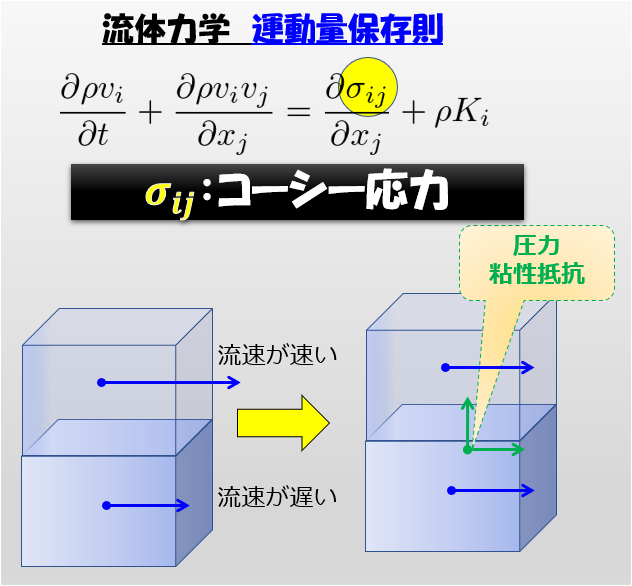
流体力学の基礎方程式であるナビエストークス方程式なども基本的には連続体として取り扱っているので、「セル内に粒子がスッカスカではないか」ってなると流体をナビエストークス方程式で扱うこと自体が理論的におかしくなっていることになります。
クヌッセン数のまとめ
さらに以下のように呼ぶこともあります。
$0.01<K_n<1$ :近連続領域
$1<K_n<10$ :近自由分子領域
計算力学技術者のための問題アプリ
計算力学技術者熱流体2級対策アプリをリリースしました。
- 下記をクリックしてホームページでダウンロードできます。
- LINE公式に登録すると無料で問題の一部を閲覧できます。
※LINEの仕様で数式がずれていますが、アプリでは問題ありません。
- 計算力学技術者の熱流体2級問題アプリ作成
リリース後も試行錯誤をしながら改善に努め日々アップデートしています。
備忘録として作成の過程を綴っています。