こんにちは（@t_kun_kamakiri）
今回は境界条件の設定ファイルに直接C++のコードを埋め込んで初期化設定を行う方法について解説をします。C++と言ってもOpenFOAMで用意されている関数を上手く使って書くため特別すごいアルゴリズムを組むわけではありません。
OpenFOAMのカスタマイズにはC++の知識に加えてOpenFOAMのAPIを理解する必要があり、初心者にとってはハードルが高いでしょう。
そこで、OpenFOAMのカスタマイズはしてみたいけど難しそうと感じている人は、まずは本記事のような直接コードを書きこむcodeStreamを試してみると良いです。
- 円筒内流れの流入境界条件を周期的に時間変化する関数として与える
- 境界条件の関数を直接コードに書き込む
前回の記事の続きです。
以前の記事では「円筒内流れ」をOpenFOAMでやってみました。
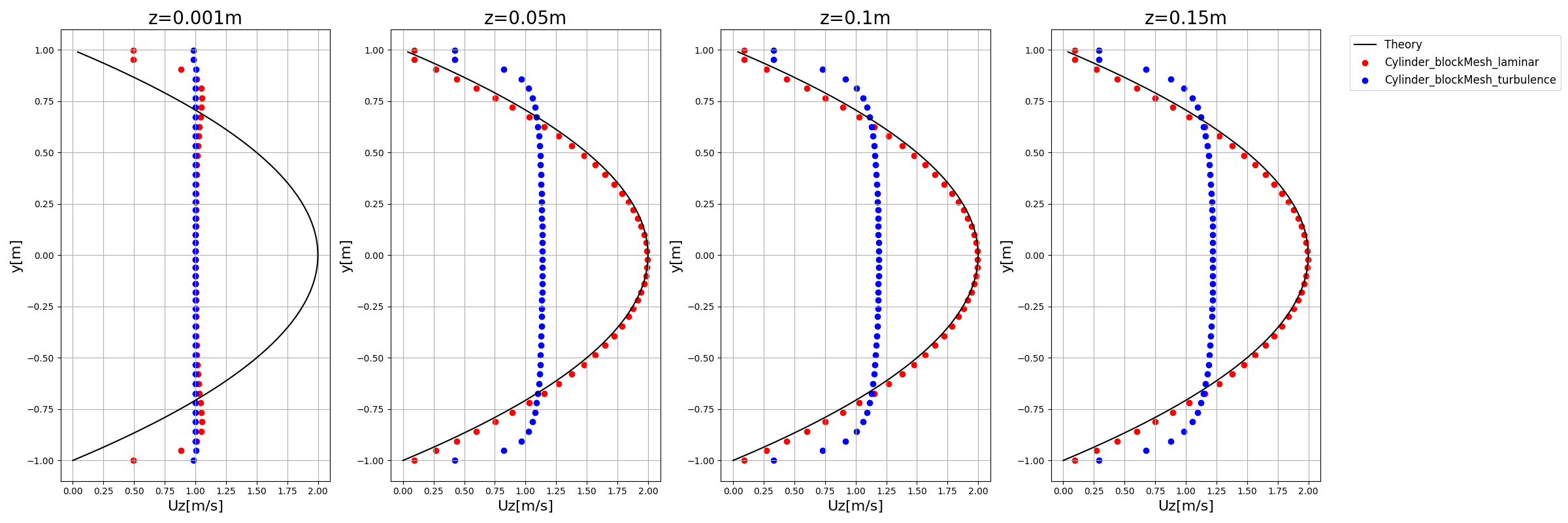
以下、blockMeshでメッシュを作成して円筒内流れを解析した結果です。
blockMeshでの結果
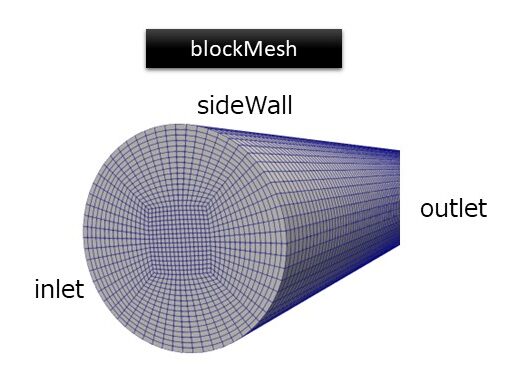
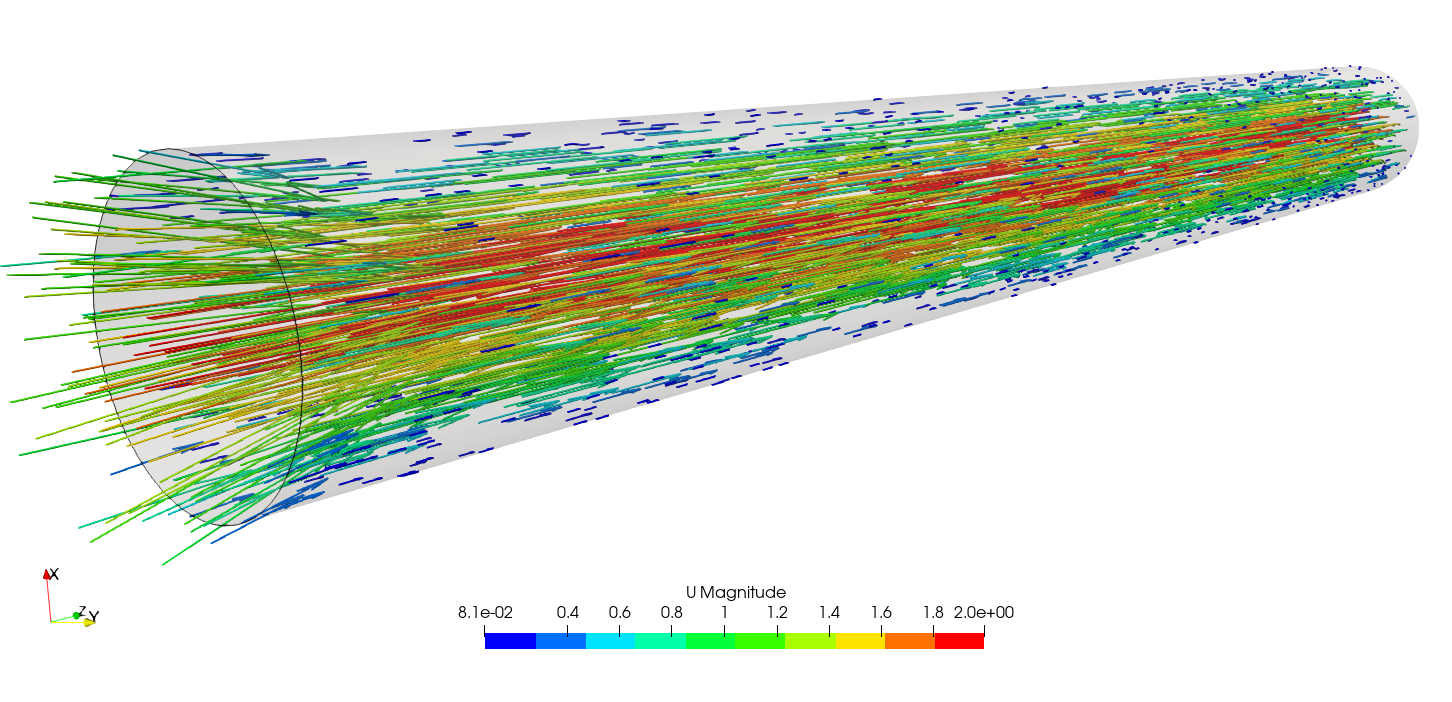
【OpenFOAM(円筒内の流れ)】blockMeshでメッシュ作成(1)
層流条件においては、流入境界での流速は1.0m/sの一定値ですが助走区間を経て徐々に2次関数で近似できるようになり、OpenFOAMの結果が２次関数と一致していることがわかります。
u=2u_{b}\bigg(1-\big(\frac{r}{R}\big)^2\bigg)\tag{1}
\end{align*}
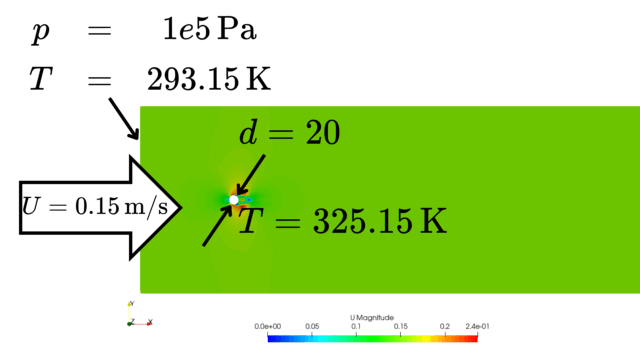
では、境界条件を以下のように時間変化する関数として与えるにはどうすれば良いのか？というのが本記事の主題です。
u=2u_{b}\sin(\omega t)\bigg(1-\big(\frac{r}{R}\big)^2\bigg)\tag{1}
\end{align*}
OpenFOAMv2012(WSL2)
モデルファイルの入手
ベースとなるモデルファイルは以下からダウンロードできます。
こちらのモデルを使って境界条件のファイル設定を書き換えます。
具体的には「0/U」の境界面の名前「inlet」の条件をcodeStreamでコードを書いて設定を行います。
今回は時間変化を解くためOpenFOAMのソルバとしてはpimpleFoamを使います。
適当なチュートリアルをコピーして、
1 | cp -r $FOAM_TUTORIALS/incompressible/pimpleFoam/RAS/pitzDaily Cylinder_blockMesh_laminar_codeStreamTime |
メッシュ情報を「円筒内流れblockMesh(層流)」で入手したものと入れ替えます。
具体的には「constant/polyMesh」を「Cylinder_blockMesh_laminar_codeStreamTime」の「constant」の中に入れます。
境界条件も入れ替えます。
「constant/turbulenceProperties」も以下のようにkOmegaSSTに変更します。
constant/turbulenceProperties
1 2 3 4 5 6 7 8 9 10 11 12 | simulationType RAS; RAS { // Tested with kEpsilon, realizableKE, kOmega, kOmegaSST, // ShihQuadraticKE, LienCubicKE. RASModel kOmegaSST; turbulence on; printCoeffs on; } |
周期的な境界条件の設定(codedFixedValue)
0/Uの境界条件を2次関数で与えます。
0/U
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | dimensions [0 1 -1 0 0 0 0]; internalField uniform (0 0 1.0); boundaryField { inlet { type codedFixedValue; value uniform (0 0 0); name inlet_BC; // codeInclude // #{ // #include "fvCFD.H" // #}; // codeOptions // #{ // -I$(LIB_SRC)/finiteVolume/lnInclude \ // -I$(LIB_SRC)/meshTools/lnInclude // #}; code #{ const scalar ub = 1.0; // 平均速度 const scalar Radius = 0.01; //半径 const scalar omegat = 1.0; // 振動数 const fvPatch& boundaryPatch = patch(); Info << "boundaryPatch.name() = " << boundaryPatch.name() << endl; const vectorField& Cf = boundaryPatch.Cf(); vectorField& field = *this; //*thisはinletの流速ベクトル scalar t = this->db().time().value(); forAll(Cf, faceI) { const scalar x = Cf[faceI].x(); const scalar y = Cf[faceI].y(); const scalar r = sqrt(pow(x, 2) + pow(y, 2)); field[faceI] = vector(0.0, 0.0, 2.0*sin(omegat*t)*ub*(1-pow(r/Radius,2) )); } #}; } outlet { type zeroGradient; } sideWall { type noSlip; } } |
以下の表を参考に関数を呼び出し必要な情報を取得します。
| Class | Description | Symbol | Access function |
| volScalarField | Cell volumes | $V$ | V() |
| surfaceVectorField | Face area vector | $\boldsymbol{S_{f}}$ | Sf() |
| surfaceScalarField | Face area magnitude | |$\boldsymbol{S_{f}}$ | | magSf() |
| volVectorField | Cell centres | $\boldsymbol{C}$ | C() |
| surfaceVectorField | Face centres | $\boldsymbol{C_{f}}$ | Cf() |
| surfaceScalarField | Face fluxes | $\boldsymbol{\phi_{f}}$ | Phi() |
今回のように、
1 2 | const scalar x = mesh.C()[i][0]; const scalar y = mesh.C()[i][1]; |
とすればセル中心の座標を取得することがでいます。
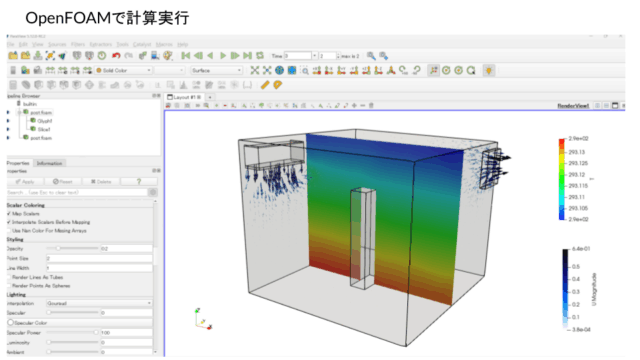
では、計算を実行させてみましょう。
1 | pimpleFoam > log.pimpleFoam & |
結果はParaViewで確認します。流入境界条件が思った通りの速度分布になっているかを確認しましょう。
※まず、いきなりこのようなコードを書くのはしんどいので、時間を取得する関数が「this->db().time().value()」が使わているチュートリアルを探します。
1 | find $FOAM_TUTORIALS -type f |xargs grep "this->db().time().value()" |
いくつか候補が出てきますので適当なファイルを開いて眺めてみると勉強になります。
1 | /opt/OpenFOAM/OpenFOAM-v2012/tutorials/combustion/XiDyMFoam/oscillatingCylinder/0/pointDisplacementy: const scalar t = this->db().time().value(); |
おすすめ参考図書
☟こちらは、OpenFOAMの日本語書籍として重宝しているわかりやすい参考書だと思います。
☟こちらもOpenFOMの古いバージョンでの和訳になります。さすがにこちらはバージョンに対する日本語でのケアはしていないので、OpenFOAMに慣れている方は購入しても良いかと思います。僕は「日本語でまとまっている内容」なので少し重宝しています。
☟以下に、もっと初心者向けの同人誌を紹介しておきます。
初心者は「ってか、まずどうやってOpenFOAMをインストールするの？」というところからつまずきがちです。
そんな時は、以下の書籍をおすすめします。
改訂新版 OpenFOAMの歩き方 (技術の泉シリーズ（NextPublishing）)
インストール方法とチュートリアルで流体解析を体験・・・ちょっと高度な解析まで解説があります。著者曰くOpenFOAMのバージョンの追跡を行いながら、書籍をアップデートするようなので安心ですね。
OpenFOAMコードの辞書的な扱いとしては以下の参考書が大変役に立ちます。
本記事ではESI版のOpenFOAMを使っているため本書のFoundation版で対応していない部分がありますが、その辺を考慮しても持っていて損はないでしょう。
Follow @t_kun_kamakiri