熱力学の意義：マクロな系を考える意義

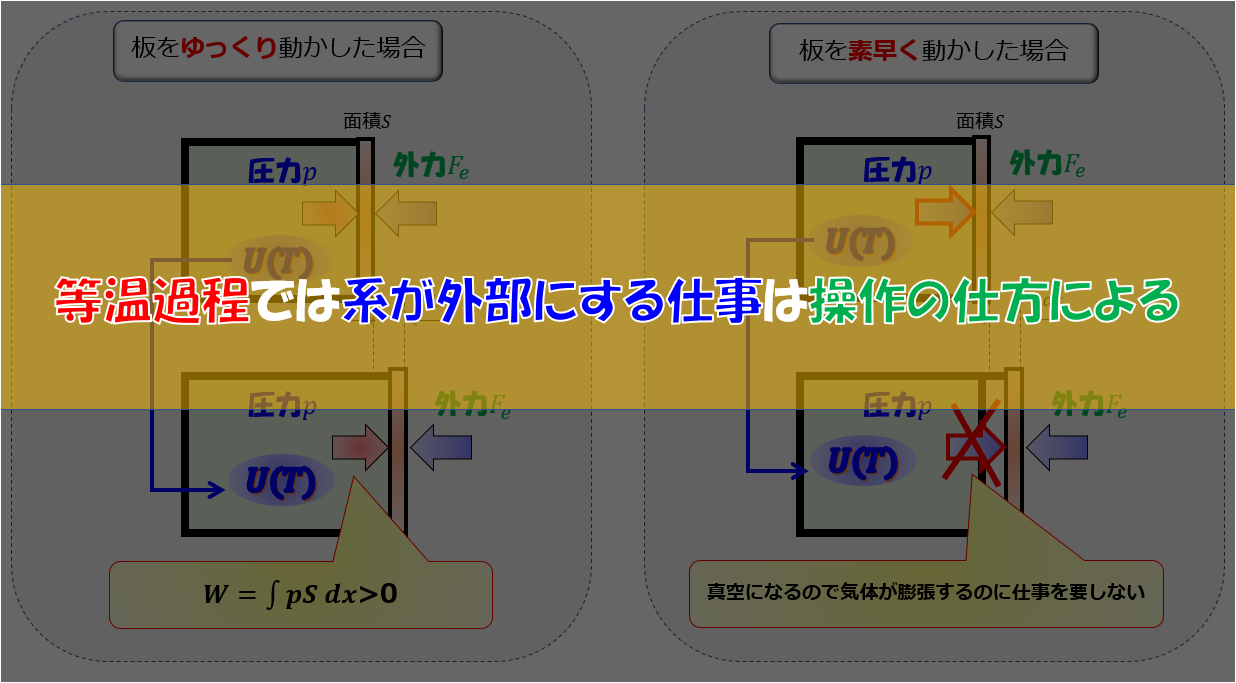
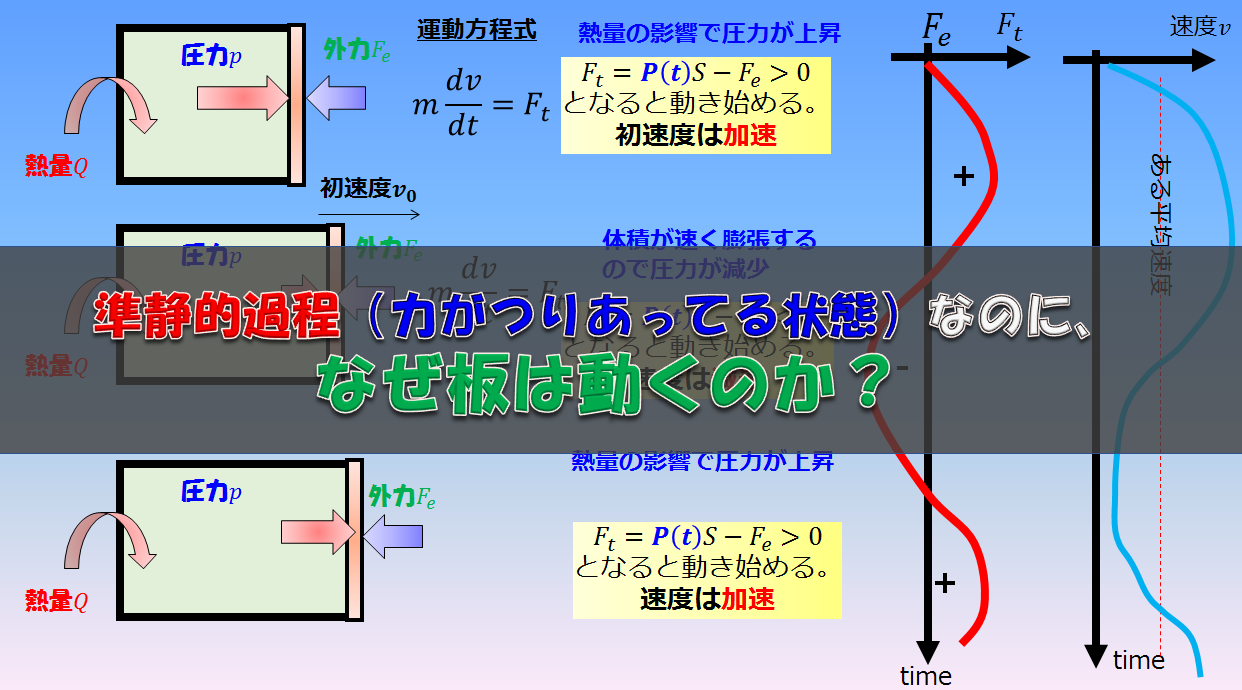
目的

物理現象をマクロな系で考えることの意義を述べたいと思います。

マクロな系とは

物理学を考えるうえで、考察の対象となるものを抽出して考えることがあります。
それを、系と呼びます。

物理学で考える基本要素は、分子、電子、原子など（中性子、陽子、さらにはクオークという話にもなるが）であり、それらは運動は基本的には量子力学の力を借りて理解することができます。

このような微視的な運動を考える系をミクロ系と呼びます。

しかし、

実現象を理解しようとして時に、ミクロな詳細の情報から、逐一調べて物事を理解しないといけないのでしょうか。

個々の分子（ここでは粒子としと呼びます）同士は、互いに相互作用しあっているのですが、それを考慮して始めて理解できるのでしょうか。

 

というのも計測器などで測定している、「圧力」「温度」などは、量子力学の力を借りてようやく理解できるものだったでしょか。

感覚的には、そんなに一生懸命に詳細を理解して計測器などが作られていると思えないですよね。

僕たちは、一体何を測定しているのかと言うと、膨大な数の粒子の運動のある時間での平均的振る舞いを計測しているのです。

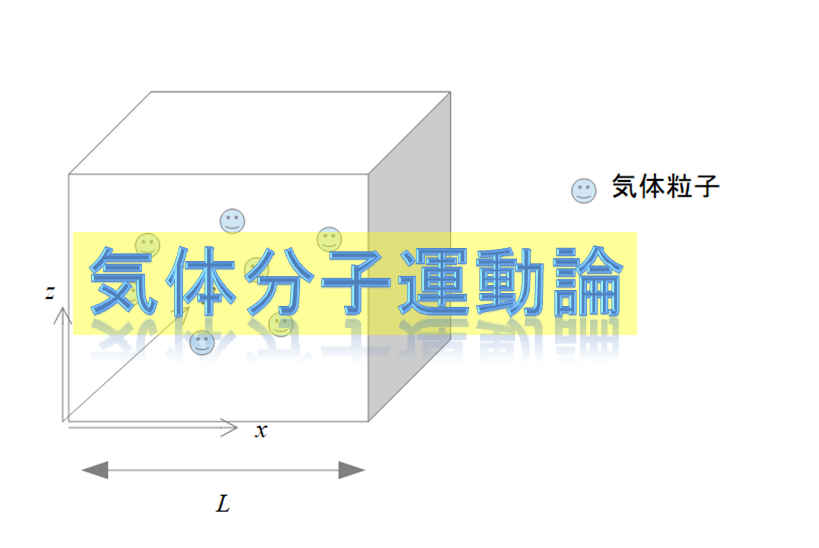
仮にそこに粒子というものが存在しているとして、下記の記事のように「気体分子運動論」でものごとを理解できます。

そのひとつひとつの粒子の数は実に膨大で、おおよそアボガドロ数個(\(6.0\times 10^{23}\)個)です。

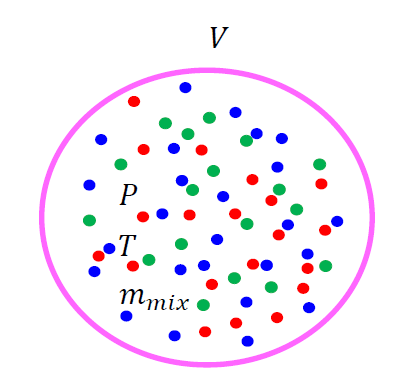
その膨大な数の粒子による系のことをマクロ系と呼んでいます。

僕たちが計測している「圧力」や「温度」は、このマクロな系での物理を計測器で測定しているのです。

マクロ系で考える意義

では、マクロ系で考える意義は何でしょうか。

熱力学は、それだけの膨大な数の粒子の平均的な振る舞いを扱う学問であります。

これは、熱力学に限った話ではありません。

統計力学、流体力学も、個々の粒子の詳細な振る舞いには興味がなく（正確には詳細を知らなくても良いという意味になる）、ある程度粗く見ることで発展した学問であると思います。

しかし、こう思う人もいるでしょう。

アボガドロ数個(\(6.0\times 10^{23}\)個)なのだから、アボガドロ数個(\(6.0\times 10^{23}\)個)の運動方程式を立てて連立方程式を、ハイパワーの計算機で解けばいいのではないかと・・・・・

これには、下記に示す2つの理由で意味がないと考えています。

1.解くことが現実的にできるのか、解いた後の処理ができるのか。

もちろん原理的には解くことはできます。無限の時間があって、いつまでの計算させておけばよいのですから。

※「原理的にはできる」は、だいたい「現実はできない」の意味になることが多い(´・ω・`)。

しかし、それだけの数の連立方程式を解くことは現実的には、不可能であります。

\(1億＝10^9\)ですよ(*_*;
地球が誕生して、おおよそ46億年です。
この\(10^{23}\)という数字がいかにすごい数字かお分かりいただけることと思います。

まず、解くのにどれだけ時間がかかるんですかーーーーっていう問題と、解いた後に僕たちは果たしてそれだけの数の情報を処理できるのでしょうかという問題があります。

2.解くこと自体に意味があるのか。

そもそも解くこと自体に意味があるのかという問題です。

物理学の力を使って知りたいことは、ある初期状態から出発して、その後の振る舞いがどのように変化するかなのですよね。

例えば、古典力学では、質点の運動を知りたいときには、「初期位置と初期速度」を指定すれば、その後の運動は運動方程式に従って解くことで理解するができます。

しかし、アボガドロ数個(\(6.0\times 10^{23}\)個)の粒子の初期位置と初期速度を毎回正確に知ることが可能なのでしょうか。

そういえば、量子力学では、位置と運動量の不確定性原理によって、どちらも正確な情報を知ることができなかったはずです。

あくまで詳細と言っている、分子などの運動は量子力学によって記述する必要があるため、位置と運動量の不確定性によってどちらも詳細に知ることができないと言えます。

では、

多少正確な位置と速度の情報は知らなくても、だいたいで知ってそれを初期状態とすれば良いではないか

と考えた場合は何が起こるのでしょうか。

粒子同士は互いに、絶えず相互作用を及ぼし合っている系であるため、ちょっとした初期状態のずれによって、その後の運動は大きく変わってくるというカオス性があるのです。

だから、毎回正確な初期状態を知ることができないうえに、知ったとして解いても詳細を見る限りでは有益な情報は得られないのです。

熱力学の意義

熱力学は、マクロな系でかつ熱平衡状態（別途詳細を記事にアップします）として扱う学問です。

散々言いましたが、そんなに詳細を追い求めても、出来ないうえに、出来たとしても、膨大な情報を前に打ちのめされるだけでしょう(笑)

むしろ、少ない情報(ここではたかだか2・3個の変数だけ）で状態を記述できれば、そちらの方が賢いやり方なのではないでしょうか。

それは、「詳細を扱っていないから、ちゃんと理解していない」と言う意味ではなく、「物理現象の本質だけを抽出して、運動を理解する」ということなのであります。

それが、マクロな系として現象を扱う意義（熱力学の意義）なのです。