必ずわかる！微分・全微分・偏微分

こんにちは(@t_kun_kamakiri)(^^)/

「必ずわかる」とかタイトルに書いてしまいましたが、基本的なことはこれだけ覚えておけばとりあえずOKというのだけを書いております。

微分・全微分・偏微分

どの分野でも必ず出てくる微分は絶対に覚えておかなくてはいけません。

しかし、難しく考える必要はありません。

微分

微分とは「単なる変化量」を表現しているに過ぎないです。

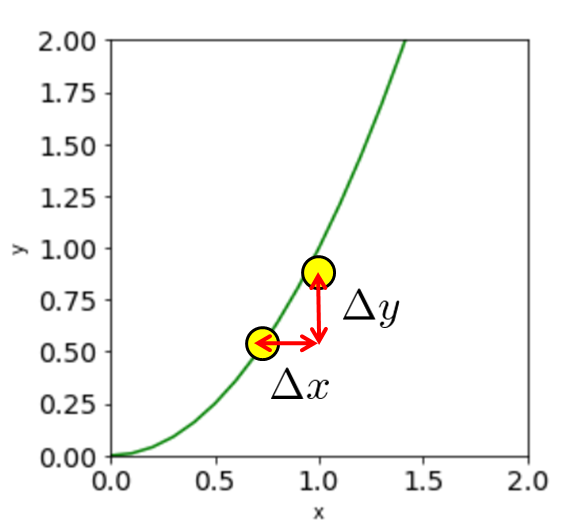
\(\Delta x\)だけ変化したときの\(y\)の変化量\(\Delta y\)を知りたい場合に微分を使います。

この変化量を数式で書くと、

ということになります。

しかし、「変化量の値が飛び飛びではないか」となります。

これでは変化量も連続的な関数として扱えないことになります。

だからこの変化量も連続な関数として扱うために、\(\Delta x→0\)の極限を取って、

と書くと、微分（正確には微分係数という）が完成します。

ここまでは高校生の範囲で習うことでしょう。

ここでの場合は、「\(y\)の変数は\(x\)だけ」という1変数関数だったのですが、2変数になったときの微分はどうなるのでしょうか。

2変数以上の微分を扱のが、偏微分と全微分という考え方です。

偏微分と全微分は大学の数学の範囲になってきます。

実は全微分と偏微分についての詳しい内容は↓下記の記事で書いています。

全微分

下記のような\(z=f(x,y)\)という変数\(x,y\)をもつ2変数関数というのを考えることにしましょう。

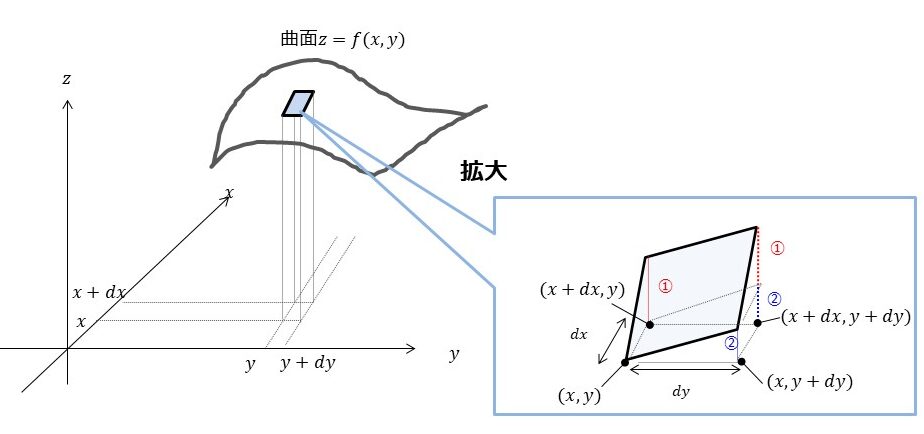
ちょっと拡大・・・・

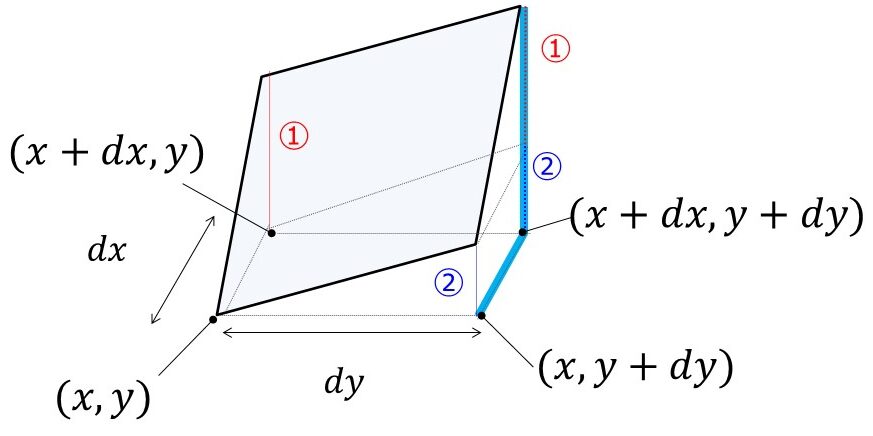
さて、全微分はこの場合は、

を意味しますね。

つまり上の絵の①＋②のことです。

\(x,y\)が微小変化したときの\(f\)の変化量ということになります。

偏微分

偏微分は「ある変数についてのみ微分を行う」というものです。

だからある変数を\(x\)とするのであれば、その他の変数（この場合は\(y\)）は固定してしまって\(x\)だけ変数だと思って微分するということです。

偏微分の場合は先ほどの全微分で使った絵を利用すればわかりやすいです。

 

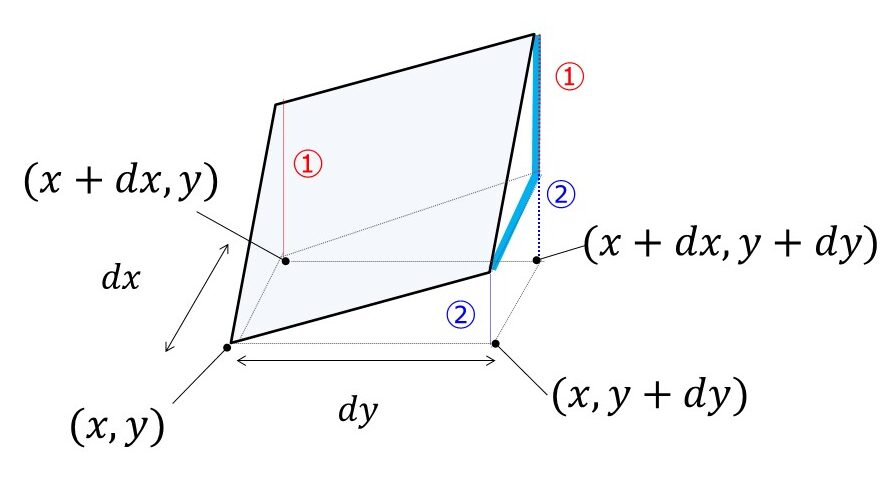
これは(4)式を使うのではなく、たんに\(y\)を固定したときの\(f(x,y)\)の変化量なので、

と書けます。

つまり変化量が①のみなので、偏微分は水色で書いた部分を見て、\(dx\)に対して①がどれだけ変化したかが「\(x\)に対する偏微分」の意味になります。

おまけ：\(x\)に対する導関数\(\frac{df}{dx}\)の場合

偏微分との違いを意識していただければと思います。

\(x\)に対する導関数というのは、

(3)式を\(dx\)で割ると、

つまり①＋②が変化量で、水色の部分を見て

が\(x\)に対する導関数ということです。

偏微分との違いはわかりますでしょうか。

偏微分は\(y\)を固定している状態で\(x\)に対して微分を行ったのですが、\(x\)に対する導関数は特に\(y\)を固定しているわけではないので、微小変化\(dy\)の変化分も足して\(x\)に対して微分を行うということです。

おすすめの参考書

最後におすすめの参考書を紹介しておきましょう。
マセマの参考書は大学初学年や、なんだったら高校生でも読めるくらいわかりやすく書かれていますので、「大学数学はキツイな」って感じた方は手に取ってみてください。