先日は、Twitterでこのようなアンケートを取ってみました。
【熱力学第一法則はどう書いているかアンケート】
Q:熱量
U:内部エネルギー
W:仕事(気体が外部にした仕事)
´(ダッシュ)は、他と区別するためにつけているので、例えば、
「dQ´=dU+dW´」は「Q=ΔU+W」と表記しても良い。— 宇宙に入ったカマキリ@物理ブログ (@t_kun_kamakiri) 2019年1月13日
これは意見が完全にわれた面白い結果ですね!(^^)!
このアンケートのポイントは2つあります。
\(W\)を気体がした仕事と見なすか?
それとも、
\(W\)を外部がした仕事と見なすか?
「\(W\)と\(Q\)が状態量ではなく、\(\Delta U\)は状態量である」とちゃんと区別しているのか?
2つのポイントを盛り込んだアンケートでした(^^)/
つまり、アンケートの「1、2」はあまり適した書き方ではないということですね。
(僕もたまに書いてしまいますが・・・)
わかりにくいアンケートだったので、表にしてまとめてみます。
まとめると・・・・
| A:ポイントその1 | B:ポイントその2 | |
| 熱力学第一法則 | 状態量と状態量でないものを区別する書き方 | |
| 1 | 熱量=内部エネルギー+気体(系)がする仕事量 | \(Q=\Delta U+W\) ※\(\Delta U\)は状態量 ※\(W\)は気体がする仕事量 |
| 2 | 内部エネルギー=熱量+外部が(系に)する仕事 | \(\Delta U=Q +W_{e}\) ※\(\Delta U\)は状態量 ※\(W_{e}\)は外部が系にする仕事量 |
以上のような書き方ならOKということです。
では、少しだけ解説していきたいと思います♪
「熱力学第一法則」と「状態量」について理解する![/box02]
内部エネルギーとは?
内部エネルギーと言われてもよくわからないかもしれませんよね。
僕もわかりません(/・ω・)/
とてもミクロな視点で見ると「粒子がうじゃうじゃ激しく運動している」状態なのかもしれませんが、熱力学という学問はそのような詳細でミクロな視点の情報には一切踏み込まずに、マクロな物理量だけで状態を物語ります。
なので、内部エネルギーは「圧力、温度などの物理量」を想像しておくことにしましょう(^^)/
では、本題に入ります。
ポイントその1:熱力学第一法則
| A:ポイントその1 | B:ポイントその2 | |
| 熱力学第一法則 | 状態量と状態量でないものを区別する書き方 | |
| 1 | 熱量=内部エネルギー+気体(系)がする仕事量 | \(Q=\Delta U+W\) ※\(\Delta U\)は状態量 ※\(W\)は気体がする仕事量 |
| 2 | 内部エネルギー=熱量+外部が(系に)する仕事 | \(\Delta U=Q +W_{e}\) ※\(\Delta U\)は状態量 ※\(W_{e}\)は外部が系にする仕事量 |
まずは、「ポイントその1」から話をしていきます。
熱力学第一法則ってなんでしょうか?
熱力学の第一法則は、熱移動に関して端的にエネルギーの保存則を書いたもの
ということです。
エネルギーの保存則を書いたものということに過ぎません。
そのエネルギー保存則を、「熱量」「気体(系)がもつ内部エネルギー」「力学的な仕事量」の3つに分解したものを等式にしたものが熱力学第一法則です。
熱力学第一法則:熱量=内部エネルギー+気体(系)がする仕事量
下記のように、「加えた熱量」によって、「気体(系)が外に仕事」を行い、余った分が「内部のエネルギーに蓄えられる」と解釈します。

それを式で表すと、
熱量=内部エネルギー+気体(系)がする仕事量・・・(1)
ということになります。
また、別の見方だってできます。
熱力学第一法則:内部エネルギー=熱量+外部が(系に)する仕事
下記のように、「外部から仕事」を行うことで、「内部のエネルギーに蓄えられ」、残りの数え漏れを「熱量」と解釈することもできます。
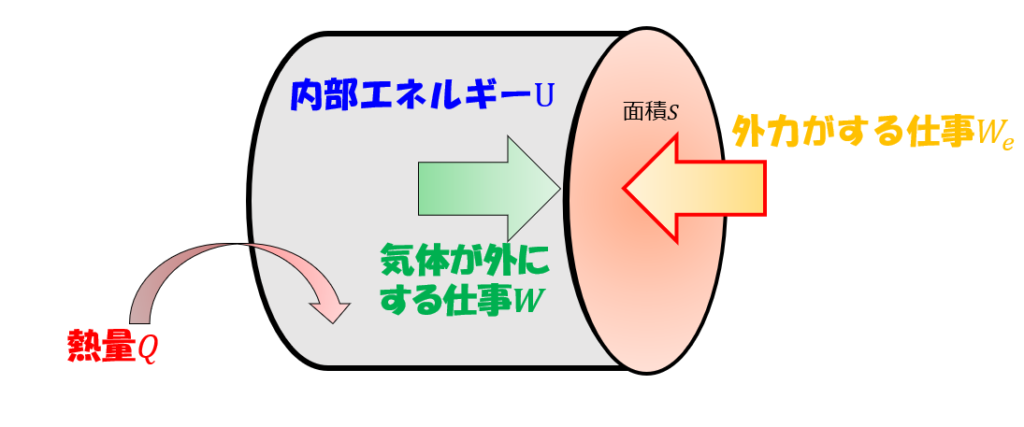

つまり・・・
内部エネルギー=熱量+外部が(系に)する仕事・・・(2)
(1)式と(2)式を見比べると、
気体(系)がする仕事量=外部が(系に)する仕事
このようでないといけないことになります。
本当にそうなのでしょうか?(/・ω・)/
そうなのでしょうけど、そうでないかもしれません・・・
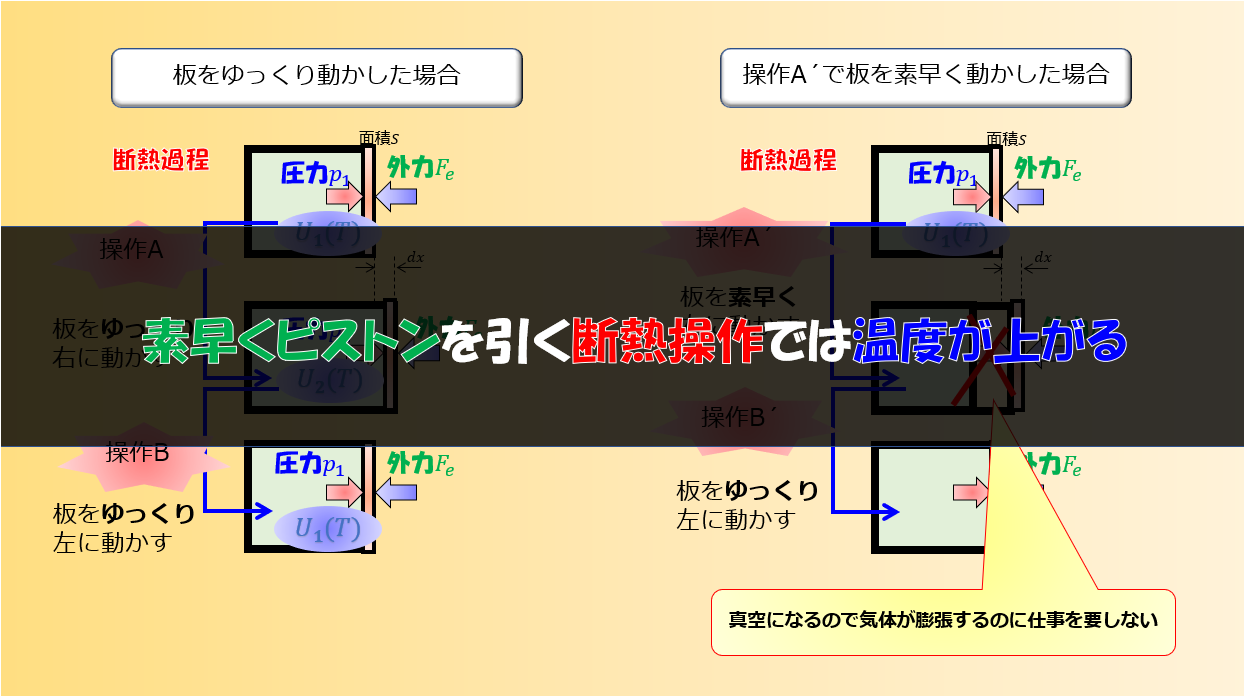
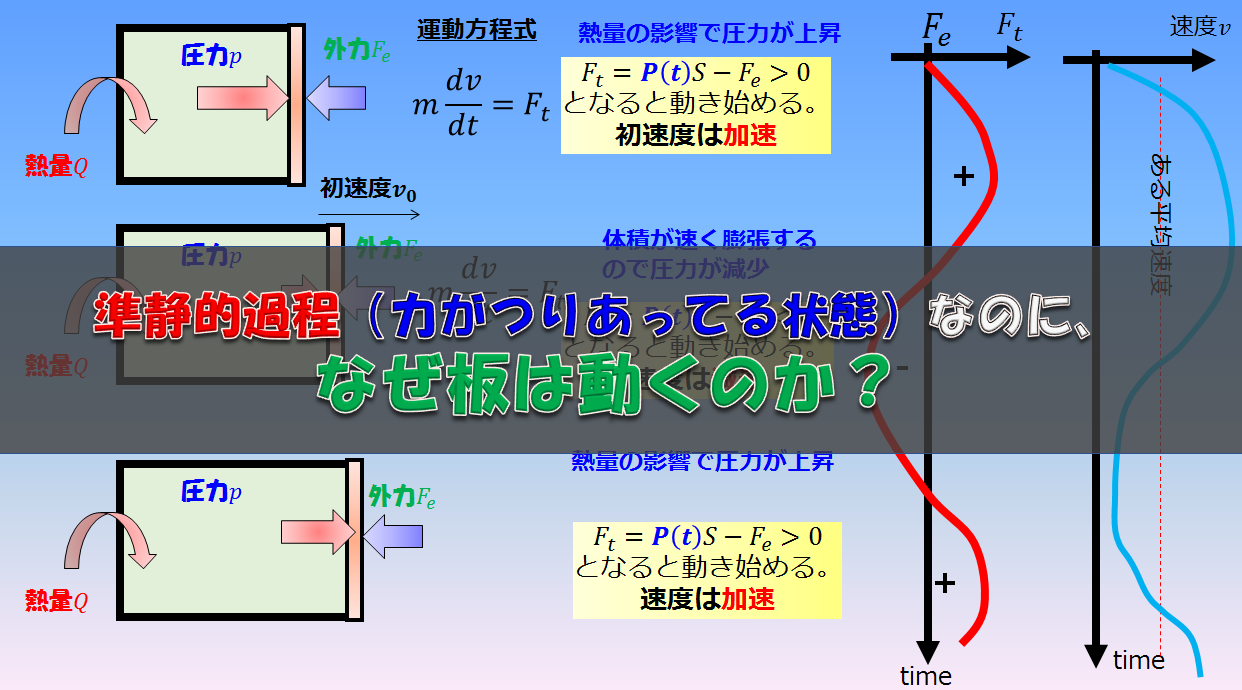
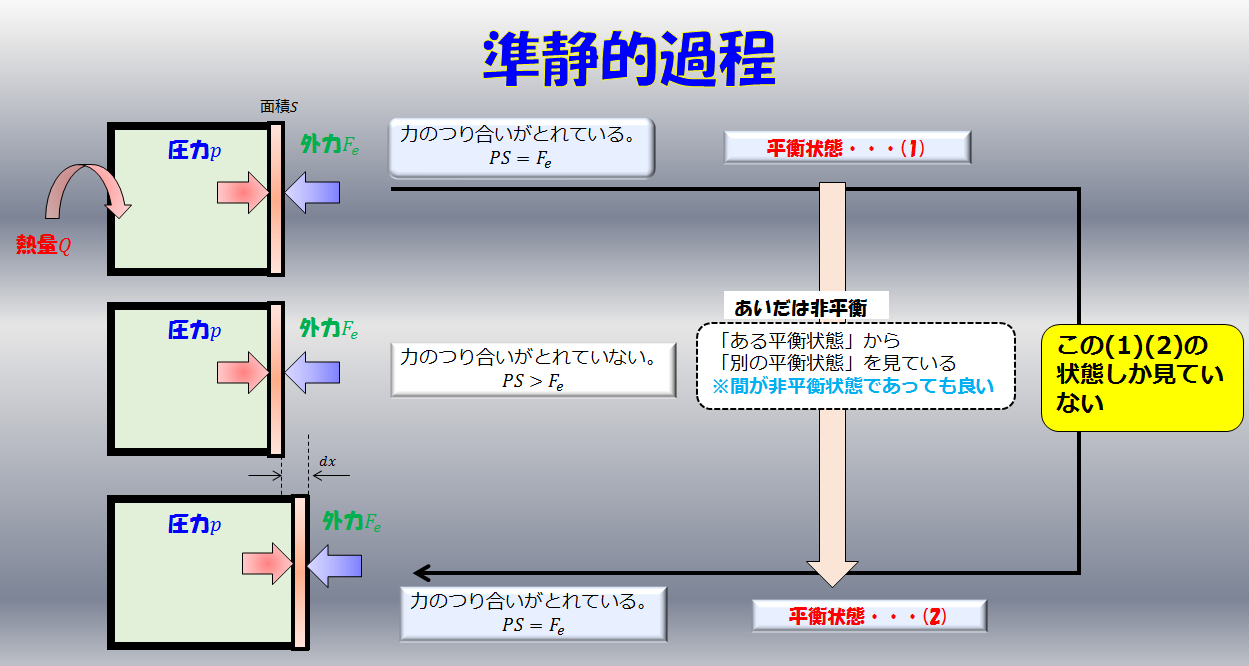
準静的過程
例えば下記のように、「熱量」を加えて気体の温度を上昇させます。
そうすると、板は徐々に右へゆっくりと動き出します。
力のつり合いをとてた状態で決して焦らずゆっくりと板を押します。
このような常に熱平衡状態が保たれていると近似できるような過程のことを準静的過程と言います。
熱平衡状態とは、「マクロな物理量である、圧力、温度など」が定まっている状態です。
こういったかなり理想的な極限での状態を仮定すると、気体の圧力が定義できているので、力学的な力のつり合い(板は動いていないと思えるくらいゆっくりなので)を立てることになります。
pS-F=0\cdot\cdot\cdot (3)
\end{align}
となります。
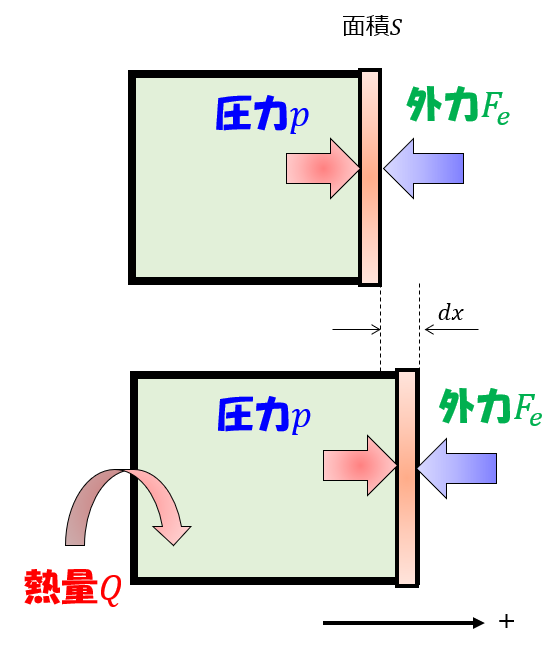

だから、これを仕事量に置き換えると、
pSdx-Fdx = 0\cdot\cdot\cdot (4)
\end{align}
W_{e}-W &=& 0\cdot\cdot\cdot (5)
\end{align}
となるので・・・・
気体(系)がする仕事量=外部が(系に)する仕事
が言えるということですね。
要するに、常に平衡状態を保っていて、気体がする仕事量も外部がする仕事量も同じ状況だから、
熱量=内部エネルギー+気体(系)がする仕事量・・・(1)
と書いても・・・
内部エネルギー=熱量+外部が(系に)する仕事・・・(2)
と書いても良かったわけです。
↓こちらに書きました。
ポイント2:状態量と状態量でないもの
| A:ポイントその1 | B:ポイントその2 | |
| 熱力学第一法則 | 状態量と状態量でないものを区別する書き方 | |
| 1 | 熱量=内部エネルギー+気体(系)がする仕事量 | \(Q=\Delta U+W\) ※\(\Delta U\)は状態量 ※\(W\)は気体がする仕事量 |
| 2 | 内部エネルギー=熱量+外部が(系に)する仕事 | \(\Delta U=Q +W_{e}\) ※\(\Delta U\)は状態量 ※\(W_{e}\)は外部が系にする仕事量 |
続いて、ポイント2についてです。
という書き方をするということです。
内部エネルギーは状態量
状態量とは、熱力学的なマクロな物理量である圧力\(p\)や温度\(T\)や体積\(V\)のみによって決定される量のことです。
だから、例えばどんな過程でその温度に達しようが、熱平衡状態に達して温度\(T\)や体積\(V\)などが定義できる状態になれば、内部エネルギーは一意的に定まります。
だから、ある状態から別の状態になったとき、熱平衡状態に達していれば、
ある状態:\(U_{1}=U_{1}(T_{1},V_{1})\)
別の状態:\(U_{2}=U_{2}(T_{2},V_{2})\)
と書けるので、その差分である\(\Delta\)を使って、
\Delta U =U_{2}-U_{1}\cdot\cdot\cdot (4)
\end{align}
のように、始点と終点の状態量だけで書けてしまいます。
ですから、内部エネルギーは熱力学の第一法則の中で\(\Delta U\)と記述しているというわけですね。
しかし、仕事量と熱量はそうはいきません。
仕事は状態量にはならない
「仕事は状態量ではない」というのは、次のようなことを意味しています。
とても簡単な例として、「断熱過程」と「等温過程」を、p-Vグラフで書いてみます。
等温過程
気体を\(n\)モルを初期体積\(V_{1}\)に入れた場合を考えます。
初期状態から、温度一定の条件下で、状態1(\(p_{1},V_{1}\))から状態2(\(p_{2},V_{2}\))に変化させたときの仕事量を計算してみましょう。
\(p-V\)は、温度一定下だと理想気体の状態方程式から、
pV=const\cdot\cdot\cdot (5)
\end{align}
で変化します。
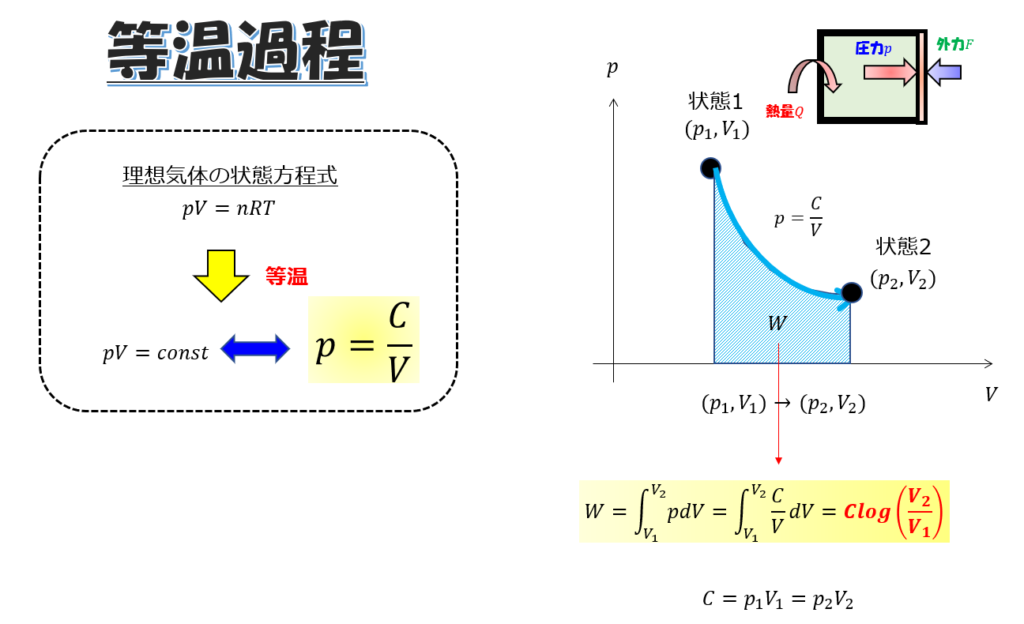

この温度一定の条件下では、気体(系)が外にする仕事量は、
W=C log\bigg(\frac{V_{2}}{V_{1}}\bigg)\cdot\cdot\cdot (6)
\end{align}
となります。
※\(C=p_{1}V_{1}=p_{2}V_{2}=nRT\)です。
断熱過程
今度は、
初期状態から、断熱の条件下で、状態1(\(p_{1},V_{1}\))から状態2(\(p_{2},V_{2}\))に変化させたときの仕事量を計算してみましょう。
※熱の出入りをさせないように断熱容器で囲んだ場合などを想定します。
\(p-V\)は、断熱の条件下だと「理想気体の状態方程式」と「熱力学の第一法則」から、
pV^{\gamma-1}=const\cdot\cdot\cdot (7)
\end{align}
で変化します。
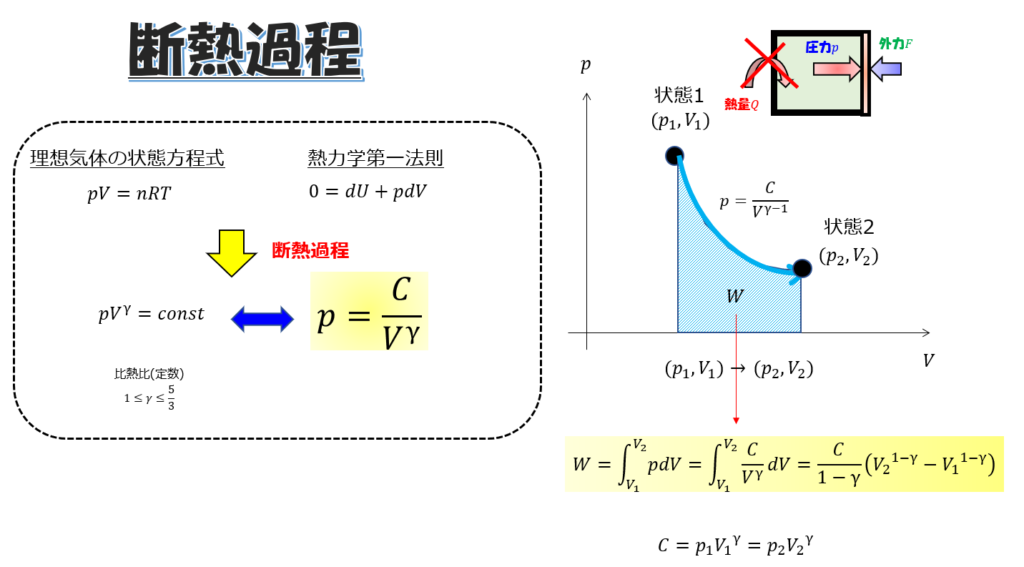

熱の供給がないので、容器を膨張させるのにはどちらかという外力を弱めていく(引くなど・・・)というような操作をすることになりますかね。
W=\frac{C}{1-\gamma}\bigg(V_{2}^{1-\gamma}-V_{1}^{1-\gamma}\bigg)\cdot\cdot\cdot (8)
\end{align}
となります。
※\(C=p_{1}V_{1}^{\gamma}=p_{2}V_{2}^{\gamma}\)です。
補足ですが、断熱過程の場合の熱力学第一法則は、
0=\Delta U+W
\end{align}
※熱量0となっているので、状態量である内部エネルギーはそのまま気体がする仕事量になります。
なので、この場合の仕事量は、始点と終点の状態量で記述できます。
結果だけ示しておきましょう!!
W=nC_{v}(T_{1}-T_{2})
\end{align}
この導出には、
- 比熱比の定義:\(\gamma=\frac{C_{p}}{C_{v}}\)
- 理想気体の状態方程式:\(pV=nRT\)
- マイヤーの関係式:\(C_{p}=C_{v}+R\)
を使います。
興味のある方は、やってみてください( `ー´)ノ
結論
(7)(8)式を見ると、仕事量がp-Vグラフのどのようなルートを通るかで結果が異なるということです(^^)/
熱量も状態量ではない
仕事量が状態量ではないことがわかりましたので、当然それと式で結びついている熱量も状態量ではないのがわかります。
あるいは次のように、「加える熱量」を考えるとわかると思います。
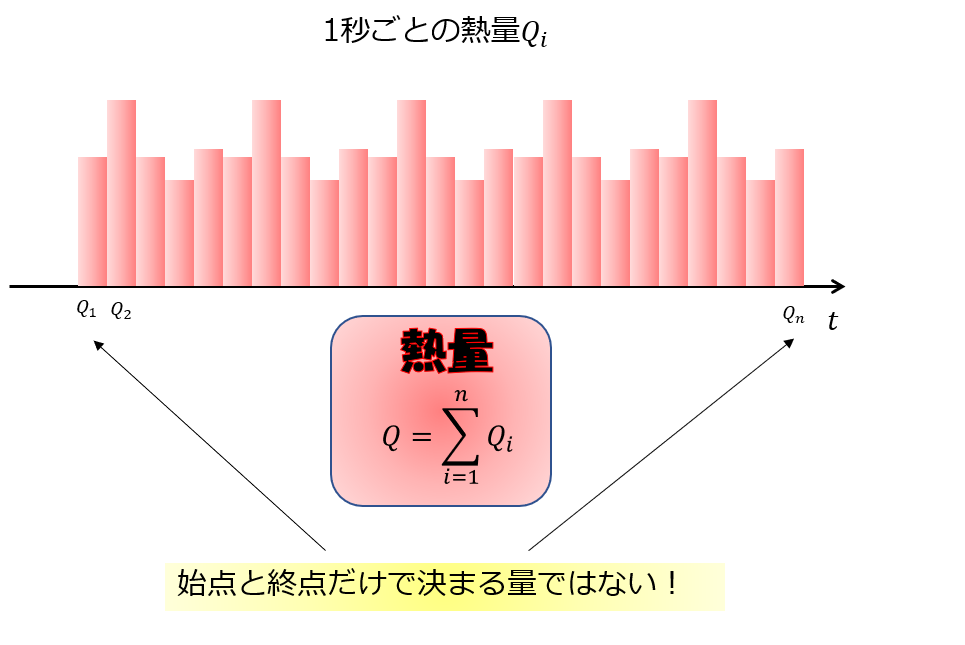

まとめ
| A:ポイントその1 | B:ポイントその2 | |
| 熱力学第一法則 | 状態量と状態量でないものを区別する書き方 | |
| 1 | 熱量=内部エネルギー+気体(系)がする仕事量 | \(Q=\Delta U+W\) ※\(\Delta U\)は状態量 ※\(W\)は気体がする仕事量 |
| 2 | 内部エネルギー=熱量+外部が(系に)する仕事 | \(\Delta U=Q +W_{e}\) ※\(\Delta U\)は状態量 ※\(W_{e}\)は外部が系にする仕事量 |
気体(系)がする仕事量=外部が(系に)する仕事
要するに、常に平衡状態を保っていて、気体がする仕事量も外部がする仕事量も同じ状況だから、
熱量=内部エネルギー+気体(系)がする仕事量・・・(1)
と書いても・・・
内部エネルギー=熱量+外部が(系に)する仕事・・・(2)
と書いてもOK!
「状態量と状態量でないものを区別」という場合に、
- 状態量:\(\Delta\)を付ける→内部エネルギー\(U\)
- 状態量ではないもの:\(\Delta\)を付けない→熱量\(Q\)、仕事量\(W\)
として、熱力学第一法則を書く。