こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
エントロピーという専門用語は、「熱力学」「統計力学」「情報理論」などでよく見かけますよね。
しばしば「エントロピーは”乱雑さの程度”」と表現されることがありました。
そういうふうに説明する人が多かっただけかもしれません。
しかし、エントロピーを“乱雑さ”と表現されるすることについては少々抵抗があります。
そこで、本記事の内容は、
「エントロピーは”乱雑さの程度”」と表現しても良いのか？
エントロピーの概念は分子の存在が確立されきる前に導入されています。
その時点ではミクロな視点を必要とする“乱雑さ”という解釈はされていませんでした。
エントロピーはマクロな視点でも専門用語として登場します。
マクロな視点を適用する理由、ミクロな視点での詳細に踏み込まなくてもマクロな物理量を予測できるからです。
では、エントロピーとはどのようなものであったのか？
それを理解するために、エントロピーの概念の導入の歴史を紹介します。
エントロピーの概念の歴史
エントロピーの概念はドイツの物理学者ルドルフ・クラウジウスによって導入されました。
熱力学では伝統的にクラウジウスの不等式を用いて、エントロピーの定義がなされています
。
そのクラウジウスの不等式はカルノーの原理の再解釈に端を発します。
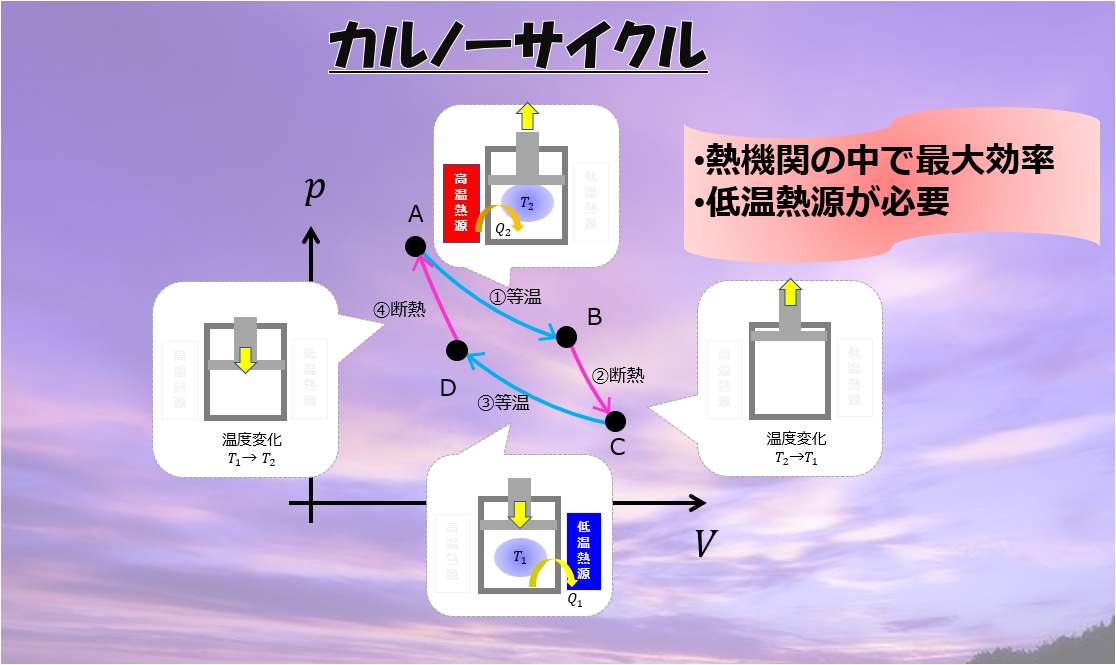
カルノーの原理
カルノーの原理とは、カルノーサイクルの熱効率は熱源の温度の比によって決まり、カルノーサイクル以上の熱効率の機関は作れないという原理です。
ここで、カルノーの原理を不可逆なサイクルも考慮した系まで拡張することを考えます。
不可逆なサイクルAが複数の熱源\(T_i\)と熱量\(Q_i\)をやり取りする装置とします。
不可逆過程ということは、熱量がその系において保存されておらず、別の熱源に漏れていることを示します。
それを式で表すと下記のようになります。
\sum_{i}\frac{Q_i}{T_i}\leq 0
\end{align*}
ちなみに等号が成り立つのは、可逆過程の時です。これをクラウジウスの不等式と呼びます。[5]
さらに、これを連続的に温度が変化するサイクルまで範囲を広げると、周回積分記号を用いて、下記のように表されます。
\oint dS=0
\end{align*}
ここで、
\frac{dQ}{T}=dS
\end{align*}
とすると、準静的過程では\(dS\)を積分して得られる値は0になることを示しています。
これは、\(S\)がどのような変化を経ても同じ状態では同じ値を取る状態量であることを示します。
このように定義された\(S\)をエントロピーと呼ぶことにしました。
このエントロピー\(S\)という量にどのような意味があるのかをもう少し考えてみます。
エントロピー\(S\)の意味を考える
断熱容器の中に温度の異なる2つの気体があるとします。
この2つの気体の間には完全に混ざり合わないように仕切り板があるとするとイメージの助けになるかと思います。
仕切り板は断熱ではないので、2つの気体の間では熱の移動が起こります。
この時、高温\(T_H\)の気体から低温\(T_L\)の気体に熱が逃げることは容易に想像できるかと思います。
つまり、高温の気体にとって熱の変化はマイナス、低温の気体にとって熱の変化はプラスとして表されます。
さらに、一度移動した熱は低温から高温に戻ることはない不可逆過程であることも付け加えておきます。
ここで、気体の温度が変わらないくらい僅かな熱が移動したとすると、エントロピーの変化は熱の変化を用いて下記のように表されます。
-\frac{\Delta Q}{T_H}+\frac{\Delta Q}{T_L}=\Delta S
\end{align*}
温度\(T\)は高温より低温の方が小さいことは自明ですので、分母が小さいことから、\(\Delta S\)の符号はプラスになります。
これは断熱系ではエントロピーが増大するというエントロピー増大則を意味しています[6]。
以上のことはカルノーサイクルの考察を通して経験的に導き出された法則です。
実はクラウジウスの不等式もエントロピー増大則も同じことを意味しており、熱力学の第二法則として知られています。
また、トムソンの法則やオストヴァルトの原理が示していることも同様に熱力学第二法則です。
例えば、第二種永久機関とは仕事をすることにより発生した熱を再度取り込みエネルギーに変えことを原理としており、これが成り立つには低温から高温に熱が移動する必要があります。
そして、これはありえないとするのがオストヴァルトの原理です。
これは比較的イメージがしやすい原理だと思いますが、言っている内容は前述したように、クラウジウスの不等式も同様であり、外部から熱が与えられない（断熱過程）ならば、低温の気体から高温の気体への熱の移動が必要な元の状態に戻ることはなく（不可逆過程）、常にエントロピーは増大することを意味しています。
オストヴァルトの原理と異なる点は、エントロピーという概念を導入しており、高温の気体から低温の気体に熱が移動した後に変化している状態を表す術を得たことです。
つまり、エントロピーとは熱の移動だけでは表現しきれないものを表すために生まれた概念なのです。
コメント
ここまでがクラウジウスが導入したエントロピーという概念の紹介です。
これより先のエントロピーという概念の解釈には、ミクロの視点が必要となってきます。
クラウジウス自身も実学としてよりイメージがしやすいようにエントロピーの解釈に取り組んでおり、そこでは分子の分散という概念が使われています。
しかし、その論文では完全にエントロピーを説明できておらず、きちんと説明ができたのはボルツマンにより統計力学を用いてからです。
それにより現在では、分子の状態数＝乱雑さとして説明されるようになりました。
ルドルフ・クラウジウスのこと① エントロピー150周年を祝って
ルドルフ・クラウジウスのこと② エントロピー150周年を祝って
熱力学第二法則
カルノーサイクル(EMAN物理学)
[5]クラウジウスの不等式(EMAN物理学)
[6]エントロピーは増大する(EMAN物理学)
お勧めの「熱力学」の参考書
まず熱力学でこの2冊を読んでおけば知識レベルは間違いないと思います。
熱力学の初学者、あるいは熱力学を苦手だと感じている方は「マセマ」の熱力学で感覚を慣らしておくのがお勧めです。
さらに、熱力学の歴史から理解したい方には「熱学思想の史的展開」がお勧めです。
エントロピーについて意味って何だろうと調査や考えがまとめられた書籍が以下です。
Follow @t_kun_kamakiri