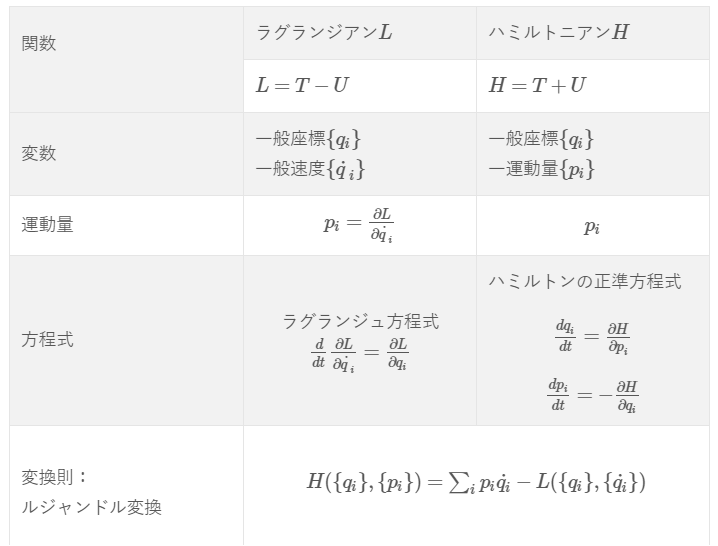
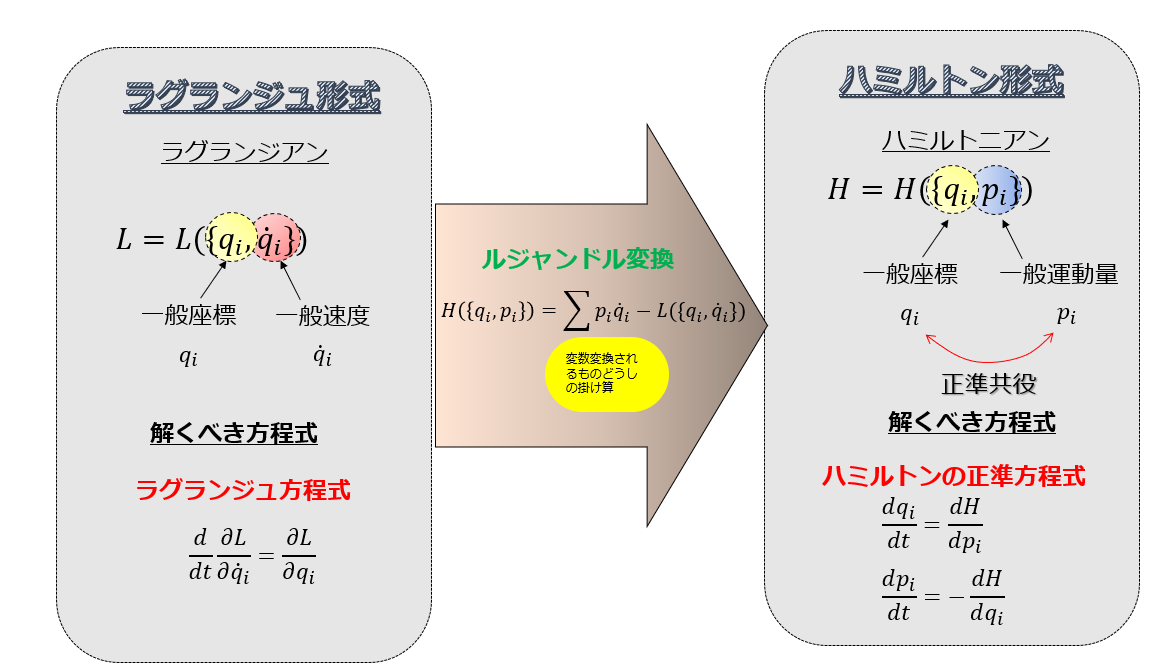
前回、ハミルトンの原理についてお話ししました!(^^)!
それで今回は、ダランベールの原理について説明したいと思います。
本記事の話の目標はこちらです。
ダランベールの原理の話をする前に、前段で仮想仕事の原理についてお話した方がわかりやすいので、
仮想仕事の原理
↓
ダランベールの原理
という流れで説明しましょうかね(^^)
ただ普通に「仮想の原理はこうだよ♪」って説明したらやはりこの記事の内容はただの参考書になってしまう(笑)
それだったら参考書を読んでくれと言わざるを得ません(笑)
ですので、違った観点を少しは交えたいです。。。
「仮想仕事の原理」を今更学んでもですね~・・・・・
当ったり前じゃないか!!
と、こうなるのですよ(笑)
悩んだ挙句、以下の3つの点も踏まえて可能な限り説明したいと思います。
- 仮想仕事の原理って何がうれしいの?
- ラグランジュ未定乗数法との関係
- 運動を束縛する力(束縛力)が複数ある場合について
それでは、まず普通に「仮想仕事の原理」の説明から始めましょう♪
仮想仕事の原理
ひとつの質点を考えましょう。
質点にかかる全ての力が釣り合っている状態(平衡状態)であるとき、以下のように書けますね。
ここで・・・・
仮想的な変位\(\delta \boldsymbol{r}_{i}\)を考えましょうと・・・・つまり、ちょ~っと動かしてやるのです。
ここでは強引に「えいっ!」って動かしたらその後の力のつり合いもクソもなくなるので、(1)状態を保ったまま仕事を仮想的にしてやるということに注意してください。
式で書くと、
実際に動かすわけではないですが、このように仮想的な変位\(\delta \boldsymbol{r}\)で動かしたときにする仕事を考えています。
(1)と(2)を考えた時に、
(1)より、
また、(2)より、
なので、
すなわち、
と、このようになります。
これが仮想仕事の原理です。
まとめると、
です(笑)
やはり何度読んでも、実に当たり前のことしか書いておらずしっくりきません。
なぜわざわざこの「仮想仕事の原理」を考えるのかよくわからないですが、僕なりに解釈したものをまとめたいと思います。
仮想仕事の原理って何がうれしいの?
まずはこれですよね(^^)
結局「仮想仕事の原理」を考えて、何か問題が簡単に解けるのであれば、仮想仕事の原理を考えることは有意義なことであります。
実は過去の僕の記事で使ったのですよね♪
それをお見せしましょう(^^)/
と、その前に・・・・
仕事をする力\(\boldsymbol{F}\)がもうちょっと具体的な方が良いので、\(\boldsymbol{F}=-\nabla U\)のような形のポテンシャルエネルギーとして考えましょう。
※重力もポテンシャルエネルギーですので重力を考えていても良いです。。
そうすると(2)式より、
が出てきましたね。
と、ここで過去の記事のお話ですが、お時間のある方は下記の記事をお読みいただきたいです。
僕は、暗に「仮想仕事の原理」とは言っていませんが、それらしい感じで解いた記事を書いたのでした。
さらっと、記事の概要を言っておきますと・・・・
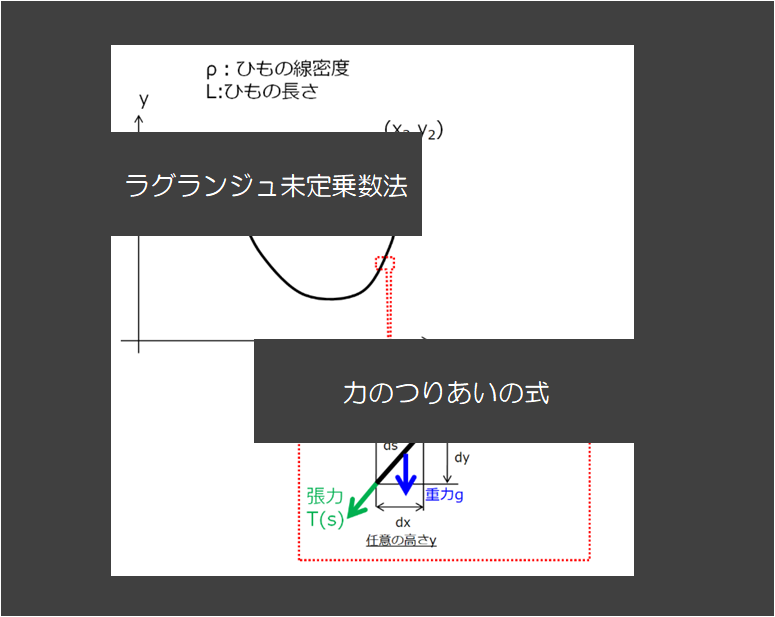
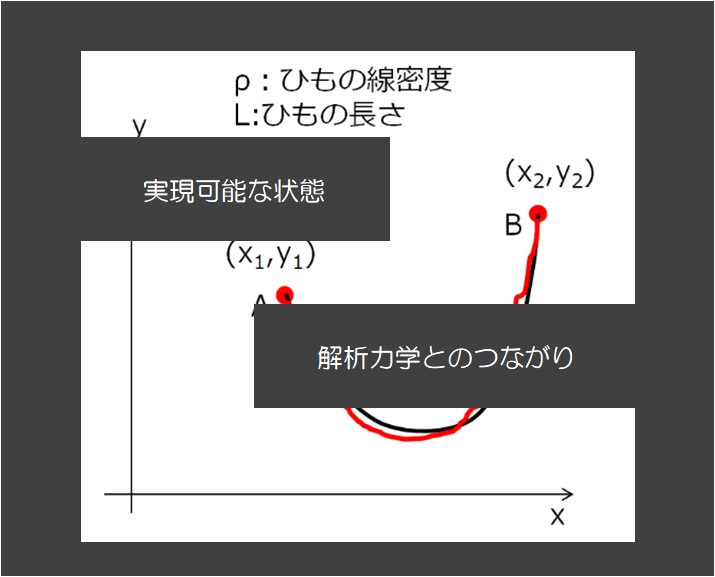
下記の絵のように、2点が固定されているひもを考えます。
そのとき、「力のつり合い(平衡状態)でのひもの形状はどのようになっているか」という問題を考えました。
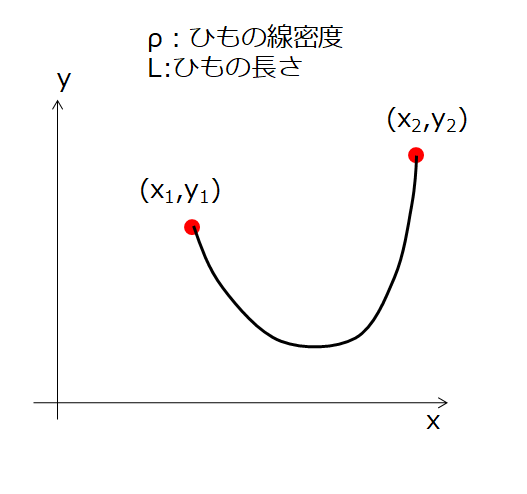
その時の僕の解法は、
ここでの、「ポテンシャルU(x,y)が最小になる状態はどのような状態」というのが仮想仕事の原理と同じ考え方です。
最小なのですから、変分\(\delta x\)、\(\delta y\)、\(\delta z\)を動かしても、差はないですよね~ってところから、
と(4)式と同じになりますので、過去の記事での問題は「仮想仕事の原理が成り立つとき」の状態はどのような状態か?として解いても良かったわけです。
では、うれしさは何か?ですが、
1.ひとつは上記のように、問題を簡単に解くことができる考え方を提供してくれることにあります。
もうひとつは、
2.途中の色々な力をあれこれ考えなくても良い点にあります。
束縛力などが働く場合は、束縛条件(この場合はひもの長さが一定)として課してやれば良いわけで、「ひもにかかる張力が~」なんて考えたら結構面倒なことになります。
それを下記の記事でトライして途中で断念したのですよ(笑)
頑張ればできるんでしょうけど・・・・
さくっと、エネルギーだけ考えて、「仮想仕事の原理」よりって考えた方が簡単なのですよね。
力だとベクトルなので各方向の力のつりあいを考えないといけませんが、仕事ならスカラーなので方向を気にする必要がなくてとてもすっきり解けます!(^^)!
ラグランジュ未定乗数法との関係
ラグランジュ未定乗数法との関係については、一瞬で解説が終わります(笑)
※ラグランジュ未定乗数法についての解説はこちらに詳しく記載しております↓
(4)式の前で、
つまり、
と、このようにしましたね。
また、質点が束縛条件にあるとき、
そこから、仮想的に変化\(\delta x\)、\(\delta y\)、\(\delta z\)としても変化はない(たとえば上の例題だと、ひもの全長は変わらない)ので、
(6)+\(\lambda\)×(8)とすると、
あらゆる仮想変位\(\delta x\)、\(\delta y\)、\(\delta z\)にたいして、(9)が恒等的に成立するのは、
となりました。
全くラグランジュ未定乗数法と同じ形だ(^^)
「仮想仕事の原理」と「束縛条件の式」を考えることで、束縛力を考えなくてもラグランジュ未定乗数法の数学の考え方で問題が解けてしまうのですよね。
運動を束縛する力(束縛力)が複数ある場合について
前回のひとつの束縛条件がある場合から、束縛条件が複数ある場合についても少し触れておきたいですね。
というのも、>>ラグランジュ未定乗数法 力のつり合いの式:解析力学とのつながり(第4.4報)の後半の問題で、束縛条件が2つ出てきて、
あれ?って思ったのですよね(笑)
だから、軽く触れておきたいのです。
さて、今束縛条件がk個あるとします。そうすると、
※式がk個ある感じですね。
そうすると、(8)式同様、仮想的に変化\(\delta x\)、\(\delta y\)、\(\delta z\)に対して、
となるだけです。
そこから、
(15)+\(\lambda_{2}\)×\(\delta g_{2}\)=0・・・・
・・・繰り返す・・・
そうすると、
あらゆる仮想変位\(\delta x\)、\(\delta y\)、\(\delta z\)にたいして、(16)が恒等的に成立するのは、
このように複数ある束縛条件に拡張できましたね(^^)
こう考えると、何も座標が\(x\)、\(y\)、\(z\)だけじゃなくて、複数個の座標の場合にも拡張が簡単にできそうです。(やりませんが・・・)
これが複数束縛条件がある場合の、ラグランジュ未定乗数法の解法の概要です。
ダランベールの原理
やっとダランベールの原理の説明ができそうです(笑)
仮想仕事の原理の理解ができたら、ダランベールの原理は簡単に理解できるのではないでしょうかね。
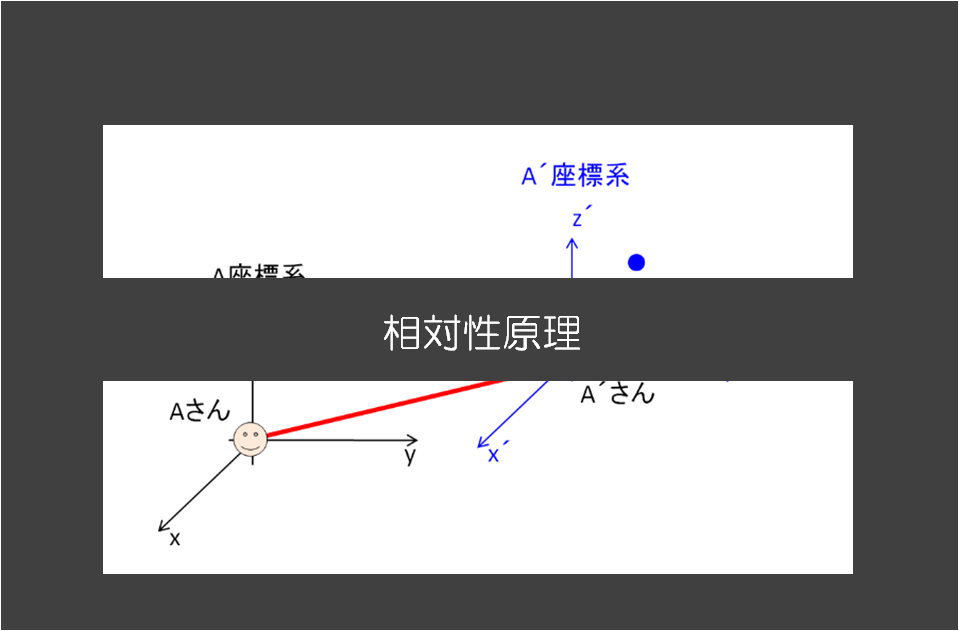
どの座標系で見るかの違いだと思います。↓こちらの説明とほとんど一緒です。
違いは仮想仕事の原理を使っているかどうかです。
例えば下記のように、電車が加速度\(a_{1}\)で動き始めている状況を考えてイメージすることができます。
電車内と電車の外での「つり革の運動方程式」を考えるのです。
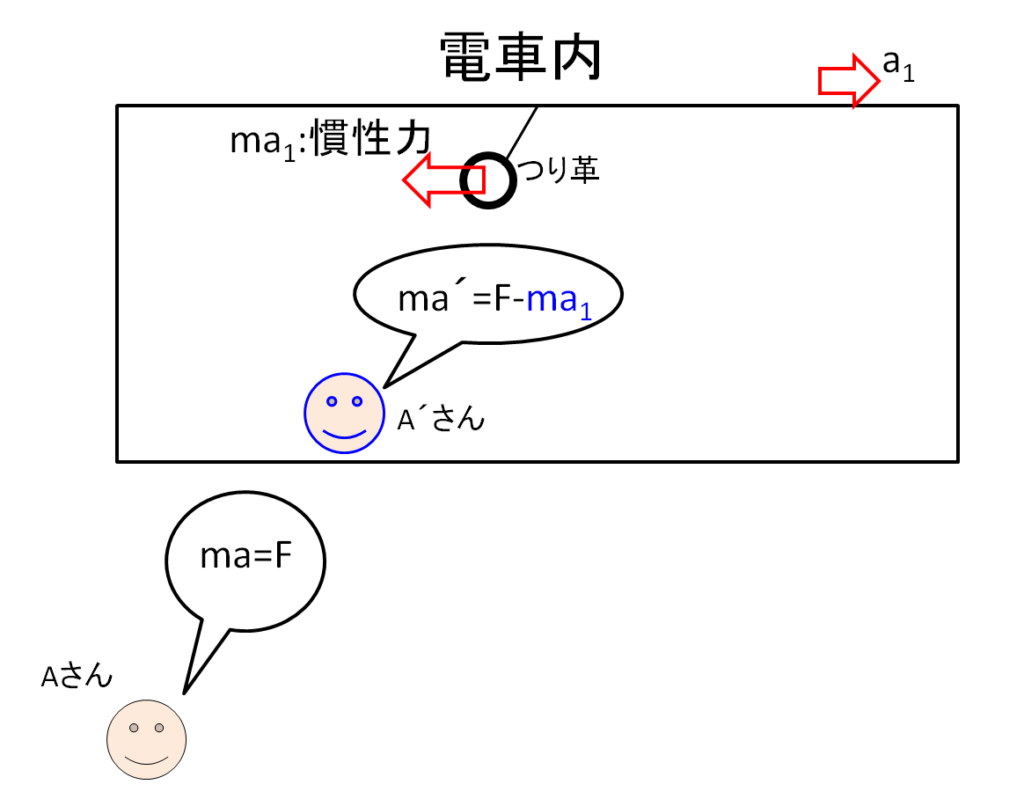
そうすると、もし\({A}’\)さんから見たときに、電車のつり革が止まっていて力のつり合いの状態(平衡状態)になっているとしたら、
\({A}’\)さんから見ると、\(F-ma_{1}=0\)のはずです。
ここでは、\(F-ma_{1}\)が全体の力のつりあい状態の式であると考えるのです。
そしたら、仮想仕事の原理より、仮想変位\(\delta x\)
3次元に拡張しておきます。
※\(\boldsymbol{a}_{1}\)は乗っている座標系の加速度
はい、これがダランベールの原理です。
終了・・・ってことですが、
ちょっと整理します。議論が少々あいまいになってしまったかもしれません(笑)
束縛がある場合
力\(F\)はこの場合、「重力」と「つり革の張力」の2つありますね。
つり革の張力は束縛力になるので束縛条件がありますね。(つり革の長さが一定)
g(x,y,z)=0・・・(22)
つまり、(8)式同様
のですね。
束縛力のある場合は、
- 「束縛力ない場合の(20)式(この場合は重力だけを考える)」
- 「(22)の束縛条件」と、分けて考える方が良いですね。
(9)、(16)式と同様の考え方で、(21)、(23)式より、
よって、
ニュートンの第二法則:運動方程式になりました(^^)/
\(\lambda\frac{\partial g}{\partial \boldsymbol{r}}\)は束縛条件から出てきたものですから、束縛力つまりつり革に働く張力になりますね。
ん?
これは\({A}’\)さんから見た運動方程式なのか、\(A\)さんから見た運動方程式なのか?
こうしといた方が誤解がなさそうだ。
\({A}’\)さんから見た運動方程式ですね。
あくまで、(22)式のg(x,y,z)=0の条件式での座標系は、\({A}’\)さんの座標系で行ったのですから。
※(21)は張力など一般的な力も含めて考えてしまっていたのですが、(25)式は束縛力とは別で考えました。
まとめ
仮想仕事の原理について説明しました。
以下の3つの点も踏まえて可能な限り説明しました。
- 仮想仕事の原理って何がうれしいの?
- ラグランジュ未定乗数法との関係
- 運動を束縛する力(束縛力)が複数ある場合について
仮想仕事の原理の考え方を用いて、ダランベールの原理の説明を行いました。
※\(\boldsymbol{a}_{1}\)は乗っている座標系の加速度
次回
本記事の話の目標の最終回です。
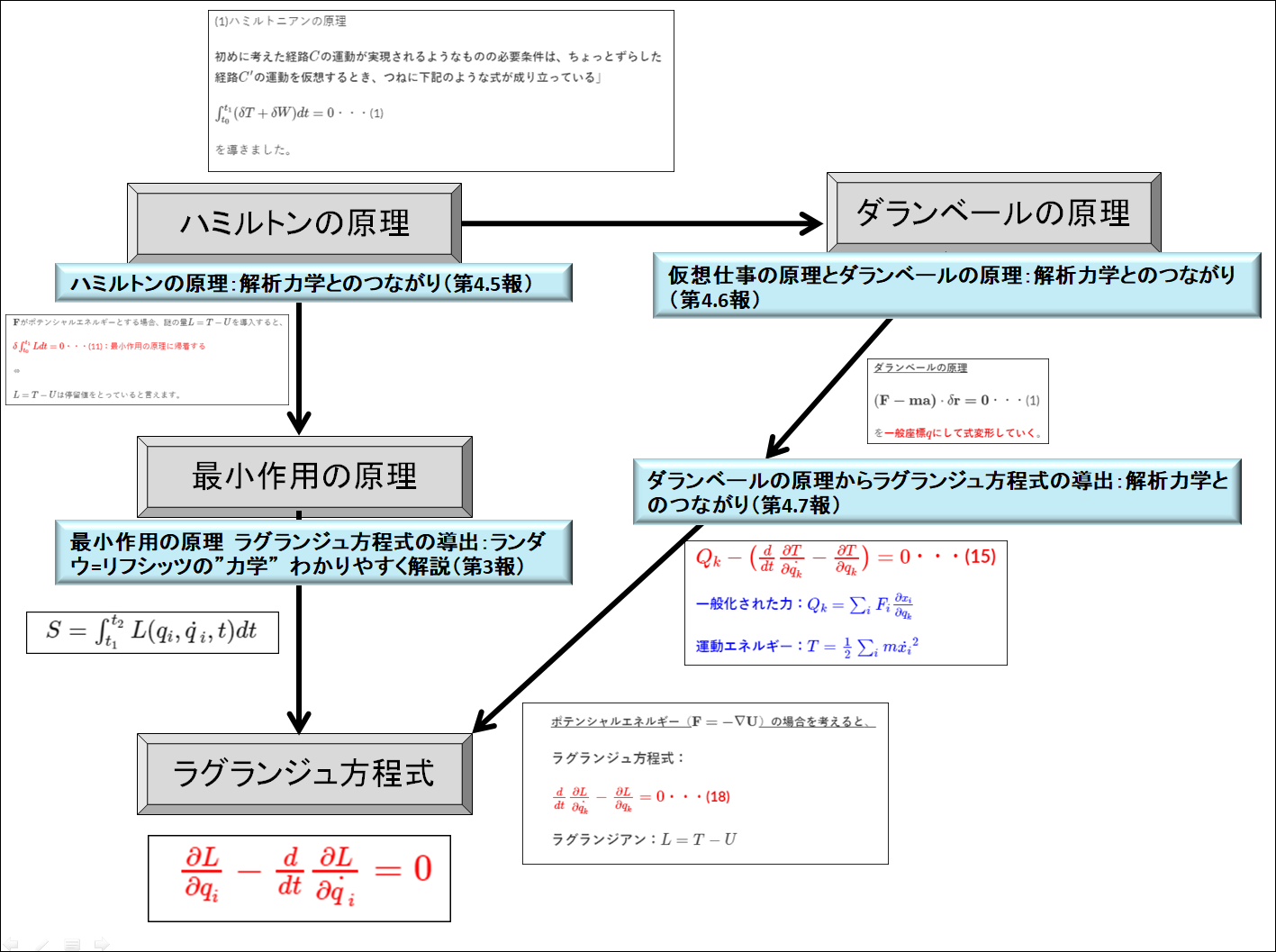
(1)ハミルトンの(変分)原理←前回の内容
↓あれ?
(2)ダランベールの原理っぽいね?←今回
↓一般座標、一般速度に変換
(3)あ、ラグランジュ方程式だ!!←次回
↓\(\boldsymbol{a}_{1}\)を\(\boldsymbol{a}\)と書きます。
のダランベールの原理に対して、一般座標系を用いたらどうなるのか?を見たいと思います。
だって、慣性抵抗\(-m \boldsymbol{a}\)って誰が決めたんだってことですから、これはあくまでデカルト座標系での慣性抵抗\(-m \boldsymbol{a}\)なので、それをベースにして一般座標系にしたらもっと一般的な形式になりそうな感じがしますよね(^^)
それがラグランジュ方程式というのが次回のオチなのですが(笑)
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ラウダウ力学
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。
大学院入試問題<物理>
比較的良問ばかりを集めているように思います(^^)/