どうも(^^)/
前回は、「ダランベールの原理」について説明しましたね。
ようやく、本記事の目標、「ダランベールの原理からラグランジュ方程式の導出」が示せます。
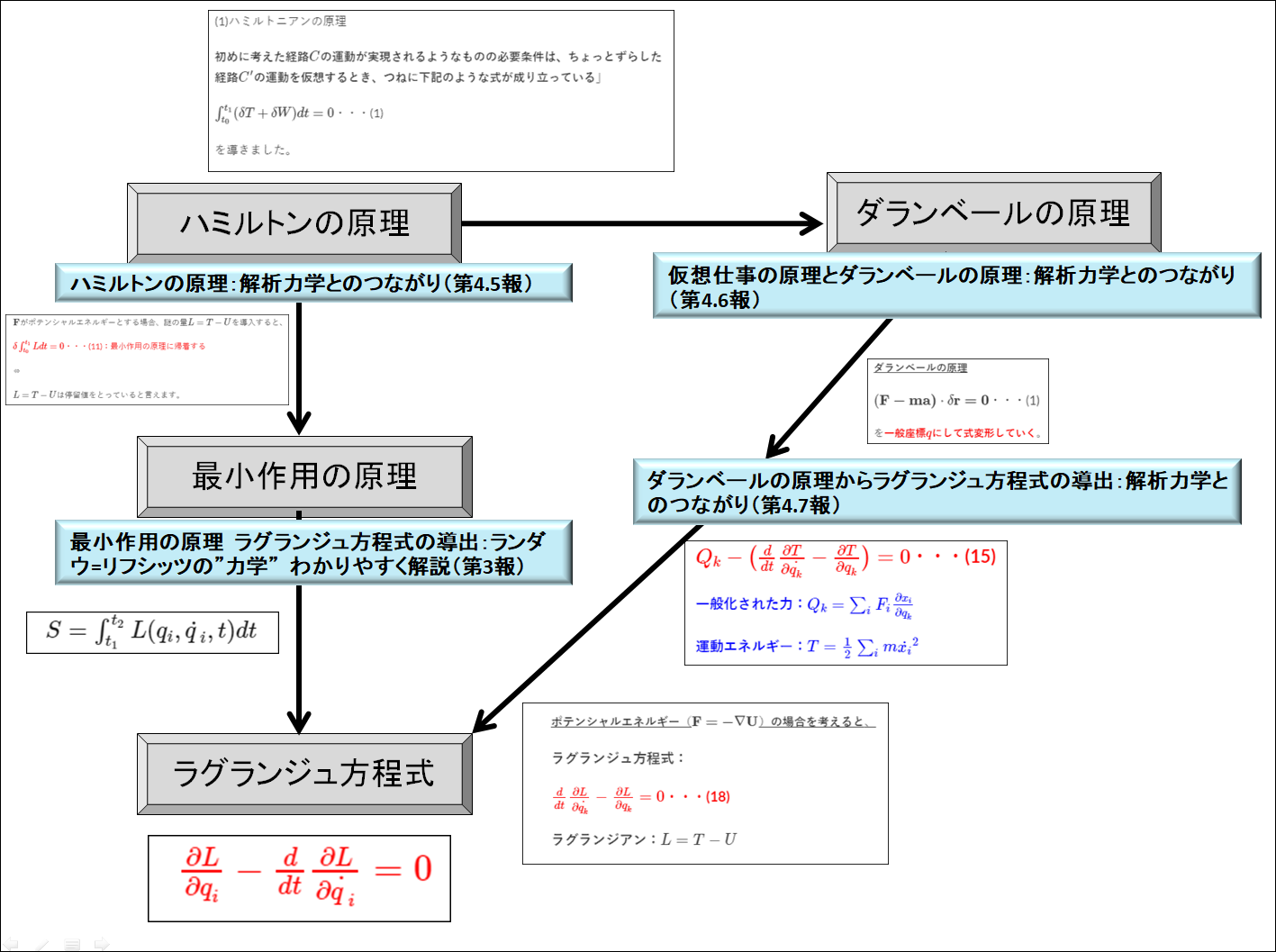
全体の流れはこんな感じで今までやってきたのですよね。
(1)ハミルトンの(変分)原理←前々回の内容
↓あれ?
(2)ダランベールの原理っぽいね?←前回
↓一般座標、一般速度に変換
(3)あ、ラグランジュ方程式だ!!←今回
それで、さっそく計算していくわけですけど、やってみて結構計算が複雑というか面倒というか(笑)
方針はこんな感じです!
ダランベールの原理
\begin{align*}(\bf{F}-m\bf{a})\cdot\delta\bf{r}=0\cdot\cdot\cdot (1)\end{align*}を一般座標\(q\)にして式変形していく。
これだけです(笑)
ダランベールの原理からラグランジュ方程式の結果
さっそく計算していくわけですが、
計算していくと途中でわけわからなくなるので結果を先に示しておきましょうかね(笑)
\begin{align*}Q=\frac{d}{dt}\frac{\partial T}{\partial \dot{q}}-\frac{\partial T}{\partial q}\cdot\cdot\cdot (\diamondsuit)\end{align*}※\(T\)は運動エネルギー、\(Q\)は一般化された力と言います。
\(Q\)は一般座標\(q\)を用いた場合の一般力と呼ばれるものです。
この場合の一般は、一般座標\(q\)に対してなのか、一般的な力という意味なのかわかりません(笑)
\(Q\)をポテンシャルエネルギー\(\bf{F}=-\nabla U\)のような形の力であれば、
(☆)はラグランジュ方程式
\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}-\frac{\partial L}{\partial q}=0\cdot\cdot\cdot (\diamondsuit\diamondsuit)\end{align*}となります。
これが結果です。
※広い意味ではポテンシャルエネルギーでなくても導けますが、ここでは割愛します。
こういった内容を下記の計算で見ていくことにしましょう(^^)/
ダランベールの原理に一般座標を導入
(1)の場合だと、ひとつの質点に対してなので、3次元におけるn個の質点でを考えましょう。
そうするとダランベールの原理は、\(i=1,2,3,\cdot\cdot\cdot\cdot,3n\)についての和になるので、
になりますね。
それから、任意の系になったとき(一般座標系)になったときに、運動を記述するのに十分な自由度というのがあります。
その数の分だけ考えれば良いはずです。
例えば、
束縛が無い場合
今、n個の質点を考えているとしましょう。
そして、それぞれの質点に対して、x,y,zの3次元があるとすると、自由度は\(3n\)ですよね。
束縛がある場合
束縛条件がr個あった場合、自由度はr個少なくなるので、自由度は\(3n-r=f\)ですよね。
ここで、自由度を\(f\)とおきます。
※n個の質点の各方向の自由度も、束縛によって減った分の自由度も全部一緒にしています。
※ちなみに別に束縛条件が無い場合として自由度を3nのままにして計算しても良いですよ。束縛条件があるとその場合は式の数が減りますね~っと言って(2)式にしているだけです。
※速度\(a=\frac{d^2 x}{dt^2}=\ddot{x}\)
一般座標系では\(f\)個考えればよいので、
と、このように書けますね。
あとは、(2)式を一般座標に変換していくだけです(^^)/
ではやっていきましょうかね。
ひとつひとつやれば良いと思います。
まずは、\(\delta x_{i}\)からいきます。

あとは、腕力にものをいわせてゴリゴリ(ウホウホ)計算していくのです。
必要なのは気合です。※慣れていればそれほどの計算でもないかもしれません。
\(\delta x_{i}\)を一般座標に変換
ダランベールの原理
\sum_{i}(F_{i}-m\ddot x_{i})\delta x_{i}\cdot\cdot\cdot (2)\end{align*}
まずは、(3)式の\(x_{i}=x_{i}(q_{1},q_{2},q_{3},\cdot\cdot\cdot,q_{k},\cdot\cdot\cdot,q_{f})\)から、
と、このようになります(笑)
いきなり過ぎましたか・・・
途中計算もやってみましょう!※k=1,2,3くらいにしときます。
↑これを計算することになるのですよね。
ここで、テーラー展開しやすいように式をいじります(足したり引いたりして・・・)
ここまできたら順番に、テーラー展開します。
第一項をテーラー展開し\(\delta q_{k}\)の2次以上の項は無視します。
ゆえに、
\(\delta x_{i}\)は完成です(^^)/
※\(i=1~3n\)、※\(k=1~f\)
力\(F_{i}\)を一般座標に変換
ダランベールの原理
続いて力についても一般座標に変換します。
の項ですね。
(4)式を用いると簡単に計算できます。
ここで、
(一般化された力)
とおけば(6)式は、
※\(i=1~3n\)、※\(k=1~f\)
加速度を一般座標に変換
ダランベールの原理
最後に加速度を一般座標に変換したらゴールが見えてきます(^^)/
↑こいつですね。
まずは、(3)式を代入。
ここで、
の部分に着目して、
を考えます。
よく見ると、右辺第一項が今回ほしい式ですので、(8)式にこれを利用しましょう。
ずいぶんとごちゃごちゃしてきました(笑)
左辺の第一項、第二項ですが、\(q_{k},\dot{q}_{k},t\)は独立で扱うならば、
と、なります。
※こちらは各自計算してみましょう(^^)/
ここまで読めたのであればきっとできるはずです(笑)
さて、(10)(11)式を用いると(9)式は、
ここで、運動エネルギー\(T=\frac{1}{2}\sum_{i}m\dot{x_{i}}^2\)を導入します。
こちらも一応計算と示しておきましょう。
少々複雑ですけども、合成微分を使っているのがおわかりですかね。
合成微分は↓こんな感じです。
今回の場合は、\(y=\dot{x}^2\)とおけばおけば理解ができることでしょう。
(13)(14)式を用いると、(12)式が運動エネルギー\(T\)を用いて、
結構大変でしたね(笑)
いよいよ情報がそろいましたので、ダランベールの原理からラグランジュ方程式の導出が完成です。
ダランベールの原理からラグランジュ方程式の導出が完成
ダランベールの原理
↓一般座標に変換
(7)、(13)式を用いると、
あとは、あらゆる微小変位\(\delta q_{k}\)に対して(14)式が恒等的に成り立つとして、
\begin{align*}Q_{k}-\big(\frac{d}{dt}\frac{\partial T}{\partial \dot{q_{k}}}-\frac{\partial T}{\partial q_{k}}\big)=0\cdot\cdot\cdot (15)\end{align*}一般化された力:\(Q_{k}=\sum_{i}F_{i}\frac{\partial x_{i}}{\partial q_{k}}\)
運動エネルギー:\(T=\frac{1}{2}\sum_{i}m\dot{x_{i}}^2\)
導けました!(^^)!
(15)式を第二種ラグランジュ方程式と言うらしいですね。
個人的には、呼び方なんてどうでもいいやって感じです。
重要なのは、ここまでの一般化された力というのは、力がポテンシャルエネルギーに限った話ではないということですよね。
では、力がポテンシャルエネルギー(\(\bf{F}=-\nabla U\))の場合を考えてみましょうか。
力がポテンシャルエネルギーの場合
一般化された力:\(Q_{k}=\sum_{i}F_{i}\frac{\partial x_{i}}{\partial q_{k}}\)を用いましょう。
最後の等式は>>全微分の考え方を用いれば良いですね。
そうすると(15)式が、
ここでポテンシャルエネルギー\(U\)は、時間\(t\)、一般速度\(\dot{q}\)に陽に依存していないので、\(\frac{\partial U}{\partial \dot{q}_{k}}=0\)であることに注意すれば、
(16)式はさらに、
と、このようにできます。
ここで、\(T-U\)を何か文字でおきたいですよね。
とでもおきましょうか。
すると、(17)式が、
\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q_{k}}}-\frac{\partial L}{\partial q_{k}}=0\cdot\cdot\cdot (18)\end{align*}
おー!!ラグランジュ方程式だ!(^^)!
\(L=T-U\)がラグランジアンだ!!
まとめ
下記のような手順を踏めば、ラグランジュ方程式が導けましたね♪
(1)ハミルトンの(変分)原理←前々回の内容
↓あれ?
(2)ダランベールの原理っぽいね?←前回
↓一般座標、一般速度に変換
(3)あ、ラグランジュ方程式だ!!←今回
\begin{align*}Q_{k}-\big(\frac{d}{dt}\frac{\partial T}{\partial \dot{q_{k}}}-\frac{\partial T}{\partial q_{k}}\big)=0\cdot\cdot\cdot (15)\end{align*}一般化された力:\(Q_{k}=\sum_{i}F_{i}\frac{\partial x_{i}}{\partial q_{k}}\)
運動エネルギー:\(T=\frac{1}{2}\sum_{i}m\dot{x_{i}}^2\)
ポテンシャルエネルギー(\(\bf{F}=-\nabla U\))の場合を考えると、
ラグランジュ方程式:
\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q_{k}}}-\frac{\partial L}{\partial q_{k}}=0\cdot\cdot\cdot (18)\end{align*}ラグランジアン:\(L=T-U\)
こちらに過去の記事も載せておきますので、ご興味ある方は順にお読みください。
※是非手を動かして計算をしてほしいです(^^)
(1)ハミルトンの(変分)原理←前々回の内容
(2)ダランベールの原理っぽいね?←前回
こう考えると、やっぱりラグランジュ方程式の形式の本質は、
「最小作用の原理」と「一般座標」だけなのかって気がしますね。
だからダランベールの原理なんて途中で考えましたけど考えやすくするためだけで、
「ランダウ=リフシッツの”力学”」で記載しているように、
いきなり「最小作用の原理から始まって、一般座標を導入します~」ってやるのが一番シンプルなのですね。
さすがランダウ=リフシッツだという感想です(^^)
↓ランダウ=リフシッツの”力学”でのラグランジュ方程式の導出の仕方はこちらに書いています。
次回
次回は、まとめ記事にしましょうかね。
結構話がごちゃごちゃしてきてよくわからなくなってきましたのでね。