ガリレイの相対性原理に対してラグランジュ方程式は変わらない。

どうも(^^)/

少しずつ解析力学の理解を深めていきたいと思います。

前回は、「ガリレイの相対性原理」について書きました。

簡単にガリレイの相対性原理を書いておきます。

ガリレイの相対性原理
慣性の法則が成立している座標系を慣性系と定義し、その座標系に対して一定速度で動いている座標系でも物理法則は同格である。
※なんでこんなに回りくどい言い方なの？って思った方は上の記事をお読みくださいませ(笑)

もう少し式の上でもまとめます↓

\(A\)座標系に対して、一定速度\(\boldsymbol{V}\)で動いている\({A}’\)座標系を考えます。

\(K\)座標系

\begin{align*}m\frac{d^2\boldsymbol{r}}{dt^2}=\boldsymbol{f}\cdot\cdot\cdot (1)\end{align*}

\({K}’\)座標系

\begin{align*}\boldsymbol{r}’=\boldsymbol{r}-\boldsymbol{V}t\cdot\cdot\cdot (2)\end{align*}

(2)を(1)に代入すると、\(\bf{V}\)は時間に対しては一定なので、

\begin{align*}m\frac{d^2\boldsymbol{r}’}{dt^2}=\boldsymbol{f}\cdot\cdot\cdot (3)\end{align*}

(1)と(3)の形が同じなので、物理法則は同格であると言えますね。

これが「ガリレイの相対性原理」です。

それでは本記事のの内容、

本記事
ガリレイの相対性原理に対して、

ラグランジアン\(L\)はどうなるの？

ラグランジュ方程式はどうなるの？

これらの問に答えようと思います(^^)

※本記事の内容は「ランダウ＝リフシッツの”力学”」の内容は同じですが、論法が少し違います。

さて、やっていきましょう(^^)/

ガリレイの相対性原理を考えた時のラグランジアンは？
(6)式に対して最小作用の原理を適応してみる
結論

ガリレイの相対性原理を考えた時のラグランジアンは？

まずはラグランジアンはどうなるかを考えましょう。

ところでラグランジアンはどのように書けるのでしたっけ？

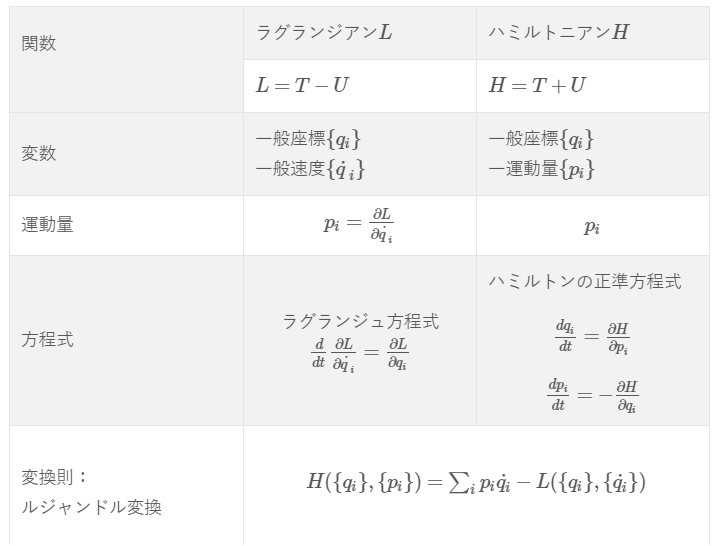
ダランベールの原理からラグランジュ方程式の導出：解析力学とのつながり（第4.7報）←こちらの記事で書きましたが、ラグランジアン\(L\)は、

\begin{align*}L=T-U\end{align*}

と、このように書けるのでしたね。

運動エネルギー：\(T=\frac{1}{2}mv^2\)

ポテンシャルエネルギー：\(U\)　（力が\(\boldsymbol{F}=-\nabla U\)のような形）

また、↓こちらにも書いたのですが、\(L=av\)（速度に比例）のような形ではないことが、最小作用の原理でわかるということを書きました。

ガリレイの相対性原理：ランダウ=リフシッツの”力学”　わかりやすく解説（第5報）

気になる方は是非お読みください。

ここでは、ひとつの質点でかつポテンシャルエネルギーも考えない場合とします。

すると、ラグランジアン\(L\)は、

\begin{align*}L=\frac{1}{2}mv^2\cdot\cdot\cdot (4)\end{align*}

となりますね。

さて、\(A\)座標系に対して、一定速度\(\bf{V}\)で動いている\({A}’\)座標系を考えた時のラグランジアン\({L}’\)はどうなるのでしょうか。

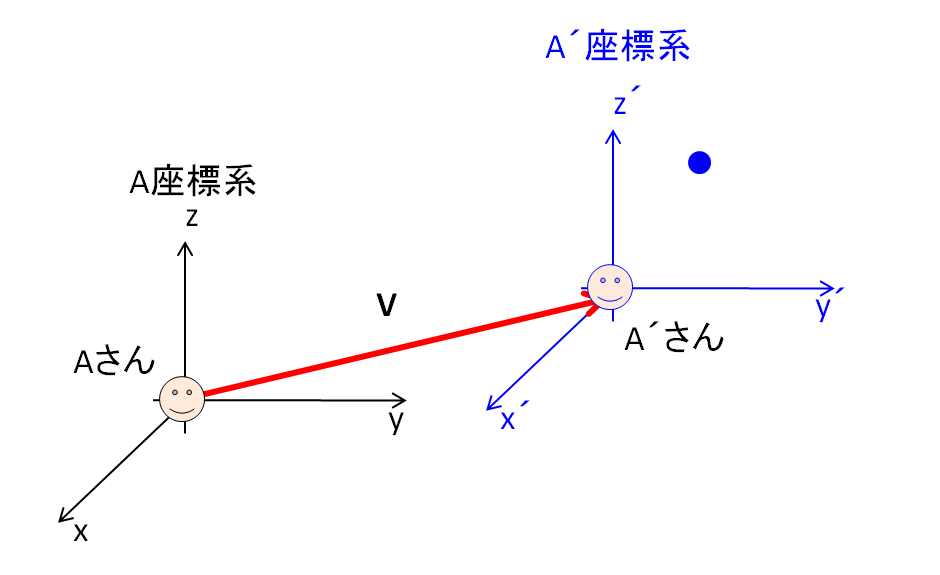
\({A}’\)座標系での質点●の速度\({v}’\)は、\(A’\)座標系から見た質点●の速度\(v\)に\({A}’\)座標系の速度\(V\)(一定値)を引けばいので、

\begin{align*}{v}’=v-V\cdot\cdot\cdot (5)\end{align*}

ですので、ラグランジアン\({L}’\)は、

\begin{align*}{L}’=\frac{1}{2}m{v}’^2=\frac{1}{2}m(v-V)^2=\frac{1}{2}m(v^2-2vV+V^2)=L+\frac{1}{2}m(-2vV+V^2)\cdot\cdot\cdot (6)\end{align*}

と、こうなりましたね!(^^)!

(6)式に対して最小作用の原理を適応してみる

\({A}’\)座標系が、速度\(V\)(一定値)で動いている場合のラグランジアンが(6)式のようになりました。

\begin{align*}{L}’=L+\frac{1}{2}m(-2vV+V^2)\cdot\cdot\cdot (6)\end{align*}

↑こんな感じでラグランジアンは\(A\)座標系でのラグランジアン\(L\)と少し変わりましたね。

でも、ラグランジュ方程式が変わらなければ、ラグランジアンは(6)式の第二項のように任意性があるということになりますね。

では、(6)式に対して最小作用の原理を適用してみましょう。

↓最小作用の原理はこちらにとても詳しく書きました。

概要を書いておきますと、下記のような作用を考えます。

\begin{align*}S=\int_{t_{1}}^{t_{2}}L(q,\dot{q},t)dt\cdot\cdot\cdot (7)\end{align*}

「\(S\)は最小にとるように系が決められている」ということが前提にあるんであれば、作用\(S\)は停留値をとっているので、\(q(t)\)をちょっとずらした場合、

\begin{align*}q(t)+\delta q(t)\end{align*}

でも作用\(S\)の変化は0のはずです。

そうすると、

\begin{align*}\delta S=\delta \int_{t_{1}}^{t_{2}}L(q,\dot{q},t)dt
\end{align*}

↓

\begin{align*}[\frac{\partial L}{\partial \dot{q}}\delta q]_{t_{1}}^{t_{2}}+\int_{t_{1}}^{t_{2}}\big( \frac{\partial L}{\partial q}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}\big)\delta q_{i}dt=0\end{align*}

ここで、\(\delta q\)というのは、スタート地点と、ゴール地点で0でしたから、上の式の第一項は消えてしまいます。

ですので、

\begin{align*}\int_{t_{1}}^{t_{2}}\big( \frac{\partial L}{\partial q}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}\big)\delta qdt=0\cdot\cdot\cdot (8)\end{align*}

↑この式に(6)式を代入したときに、出てくる式がラグランジュ方程式\(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}-\frac{\partial L}{\partial q}=0\)であれば、(6)式のようにラグランジアンは任意性があるということですね(^^)

今考えているラグランジアンは\({L}’\)なので、(6)式より

\begin{align*}L={L}’-\frac{1}{2}m(-2vV+V^2)\end{align*}

として、(8)に代入しましょう。

言ってもめっちゃ簡単です(笑)

\begin{align*}\frac{\partial L}{\partial q}=\frac{\partial {L}’}{\partial q}\end{align*}

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}=\frac{d}{dt}\frac{\partial {L}’}{\partial \dot{q}}-\frac{d}{dt}\big(\frac{1}{2}m(-V)\big)=\frac{d}{dt}\frac{\partial {L}’}{\partial \dot{q}}\end{align*}

なので、(8)式は結局、

\begin{align*}\int_{t_{1}}^{t_{2}}\big( \frac{\partial {L}’}{\partial q}-\frac{d}{dt}\frac{\partial {L}’}{\partial \dot{q}}\big)\delta qdt=0\end{align*}

のように(8)式になりましたね(笑)

ということは、(6)式のようにラグランジアンが\({L}’\)になったとしても

ラグランジュ方程式はただ\(\frac{d}{dt}\frac{\partial {L}’}{\partial \dot{q}}-\frac{\partial {L}’}{\partial q}=0\)

となるだけなですね。

形が変わらないです(^^)

結論

結論
ガリレイの相対性原理に対して、
ラグランジアンはどうなるの？
⇒

\begin{align*}{L}’=L+\frac{1}{2}m(-2vV+V^2)\cdot\cdot\cdot (6)\end{align*}

ラグランジュ方程式はどうなるの？
⇒

\begin{align*}\frac{d}{dt}\frac{\partial {L}’}{\partial \dot{q}}-\frac{\partial {L}’}{\partial q}=0\end{align*}