こんにちは(@t_kun_kamakiri)
本記事では、以下の内容のように球体周りの流れをOpenFOMAでシミュレーションするための解説をしていきます。
複数回に分けて記事を書いていくため流体解析に興味があり、自宅PCで解析してみたいという方は最後までお付き合いください_(._.)_
本記事は前回行った球体周りの流れの流入条件を変えて抗力係数とレイノルズ数の関係を実験データと比較します。
流入条件の変更はPythonを使って自動計算させます。
ただ、OpenFOAMで球体周りの流れをシミュレーションするだけではなく、文献値がある抗力係数との比較もおこなうことで数値シミュレーションの妥当性検証も行います。
今のモデルだと高レイノルズ数領域で厳しくなりますね。 https://t.co/MrIWrC6FM2 pic.twitter.com/2nIrm4ZC8I
— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) February 10, 2022
以前Twitterで投稿したときからモデルを修正してここまで合わせることができました。
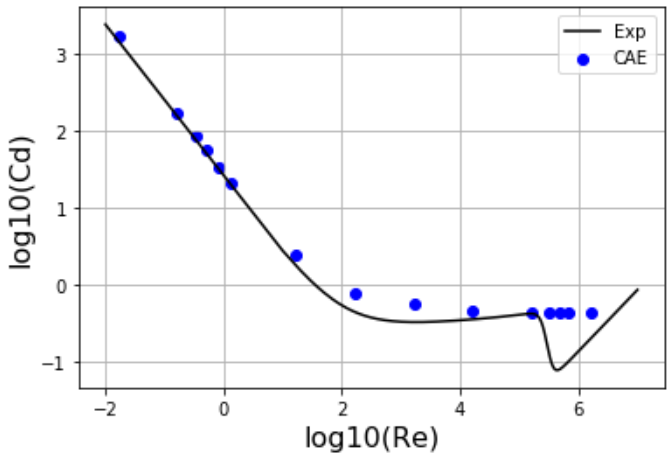
高レイノルズ数領域はノートPCでの計算負荷が大きいため再現することを断念しましたが、おおむね広い範囲でレイノルズ数と抗力係数の傾向をとらえています。
本記事のシリーズは流体解析のスペシャリストを対象にしておらず、むしろ初学者でOpenFOMAを触り始めた人が「まずは自身で触りながら解析をしたい」と思ったときに使う題材としたいと考えています。
こんな方はどうぞ
- 商用流体解析ソフトは触ったことがあり境界条件の意味などの説明は必要ない方
(CFD歴1か月以上) - Linuxでターミナルを立ち上げてCUI上でディレクトリ間を移動できる方
- 上記の経験はないが資料をもとに自分でコツコツやることが出来て分からないことがあっても心を折られない方
逆にこんな方は向いていないかもしれません
- 1~10までわかりやすく教えてもらいたい方
- 自分の質問には全部答えてほしい方
- 自分で資料などを見て勉強する気はない方
- 進行に間違いがあったときに気分が悪くなる方
過去にXsimというWeb上で解析設定が行えるサービスを使って球体周りの流れを解析するという記事をアップしました。
本記事よりももっと「ポチポチ」とボタンを押すだけでかいせきができるので不安な方はこちらの記事から始めてください。
使用環境
- FreeCAD0.19(Windows11)
- Paraview5.19(Windows11)
- OpenFOAMv2006(WSL2)
- Python 3.8.1(WSL2)
OpenFOAMとPythonはWSL2で行い、モデル作成(FreeCAD)と可視化(Paraview)はWindows上にインストールして使用しています。
抗力係数とレイノルズ数の関係
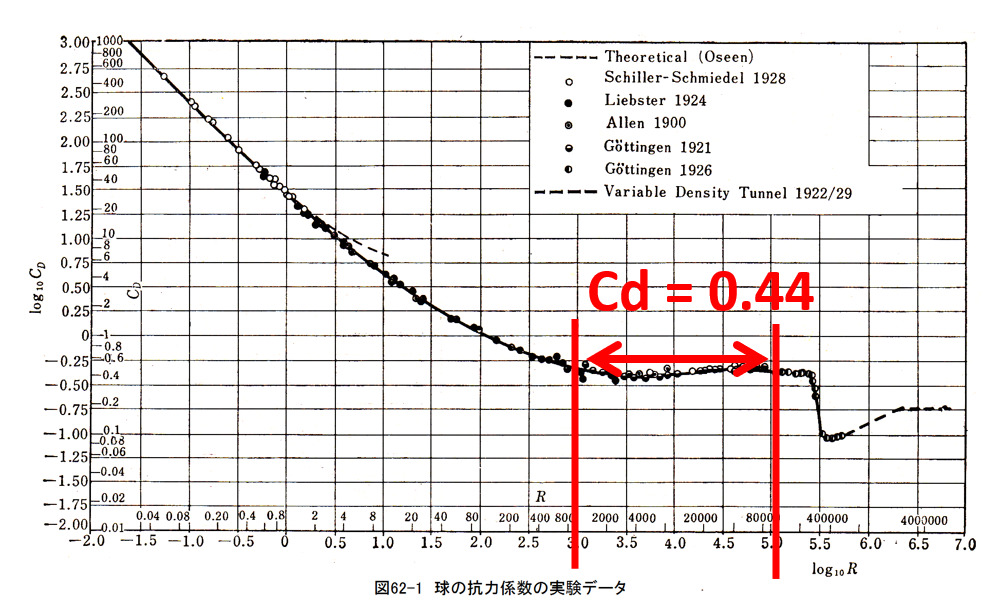
球体周りの流れに対して抗力係数とレイノルズ数の関係は以下のような実験データがあります。
\left\{\begin{matrix}
&乱流モデル使用なし:Re \leq 1000 \\
&乱流モデル(標準 k-\epsilon)Re > 1000
\end{matrix}\right.\tag{1}
\end{align*}
乱流エネルギーと乱流散逸については流入速度に応じて以下のように算出しています。
例えば流入速度が1m/sの場合は以下のような結果となります。


Pythonコード
Pythonコードはjupyter labを使ってOpenFOAMの自動計算と抗力係数の出力までを自動計算させています。
必要なライブラリと関数のコードを書きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 |
from pathlib import Path import shutil import subprocess import numpy as np from PyFoam.RunDictionary.ParsedParameterFile import ParsedParameterFile import matplotlib.pyplot as plt import pandas as pd import os def clone_file(orgCase, resultDir): "orgCaseをresultDirに重複しないようにコピー" baseName = Path(orgCase).name addName = None if addName!=None: baseName += f'_{addName}' Path(resultDir).mkdir(exist_ok=True, parents=True) n=0 newCase = Path(resultDir) / f'{baseName}_{n}' while newCase.is_dir(): n += 1 newCase = Path(resultDir) / f'{baseName}_{n}' shutil.copytree(orgCase, newCase) return newCase def cd_result(resultDir, newCase): #抗力係数の出力 keys = ['forceCoeffs'] startTime = 0 datfile = 'forceCoeffs.dat' key = keys[0] df = pd.DataFrame() case = str(newCase) name = os.path.basename(case) forceFile = f'{resultDir}/{case}/postProcessing/{key}/{startTime}/{datfile}' df_cd = pd.read_csv(forceFile, sep='\t', header=8,index_col=0) cd = np.array([ valStr for keys, valStr in df_cd[df_cd.columns[1]].items() ]) return cd def new_parameter(newU, newCase): # 流速の変更 fileU = ParsedParameterFile(newCase / '0/U') fileU.content['boundaryField']['XMin']['value'] = 'uniform ({:.6f} 0 0)'.format(newU) fileU.content['internalField'] = 'uniform ({:.6f} 0 0)'.format(newU) fileU.writeFile() print(f'Inlet(Xmin) U is now {newU}') print(f'Inlet(initial) U is now {newU}') # 抗力係数の代表速度の変更 file_controlDict = ParsedParameterFile(newCase / 'system/controlDict') file_controlDict.content['functions']['forceCoeffs']['magUInf'] = newU file_controlDict.writeFile() U = newU L = 250E-3 nu = 1.511e-05 Re = U*L/nu if Re <= 1000: fileturb = ParsedParameterFile(newCase / 'constant/turbulenceProperties') fileturb.content['simulationType'] = 'laminar' fileturb.writeFile() print(f'乱流モデルなし:Re={Re}') else: # 乱流エネルギーの計算 Intensity = 1/100 # 1% k_E = 3/2*(Intensity * newU)**2 filek = ParsedParameterFile(newCase / '0/k') filek.content['internalField'] = 'uniform {:.10f}'.format(k_E) filek.writeFile() print(f'乱流強度{Intensity*100}%:',f'k = {k_E}') # 乱流エネルギーの計算 L = 4 # boc幅一辺 4mm C_mu = 0.09 ratio_l = 10/100 # 10% epsilon= (C_mu**(3/4) * k_E**(3/2))/ (ratio_l * L) fileepsilon = ParsedParameterFile(newCase / '0/epsilon') fileepsilon.content['internalField'] = 'uniform {:.10f}'.format(epsilon) fileepsilon.writeFile() print(f'乱流散逸{epsilon}') def cd_Re(newU, cd): U = newU L = 250E-3 nu = 1.511e-05 Re = U*L/nu # print(f"cd={cd[-1]}") # print(f"レイノルズ数={round(Re,1)}") return Re def Allrun(newCase): "Allrunを実行" out_run = subprocess.check_output(['./Allrun'], cwd=newCase) return out_run.decode() def Cd_Re(): Re_ana = np.linspace(0.01, 10000000, 1000000) cd_ana = 24/Re_ana + ( 2.6*(Re_ana/5) )/(1+(Re_ana)**1.52) + ( 0.411*(Re_ana/263000)**(-7.94) )/(1+(Re_ana/263000)**(-8.00)) +(Re_ana**0.80)/461000 return Re_ana, cd_ana |
orgCaseには「Allrun」スクリプトを用意しておきます。
↓こちらはPythonではなくシェルスクリプトです。
Allrun
|
1 2 3 4 5 6 7 8 9 |
#!/bin/sh cd ${0%/*} || exit 1 . $WM_PROJECT_DIR/bin/tools/RunFunctions decomposePar mpirun -np 4 simpleFoam -parallel reconstructPar rm -rf ./processor* |
流入速度を変えてパラスタするため、速度のリストデータを用意します。
|
1 2 3 4 |
orgCase = 'orgCase/base_k-epsilon' resultDir = 'resultDir' newU_list = [0.000001,0.00001,0.00002,0.00003, 0.00005, 0.00008, 0.001, 0.01, 0.1, 1.0, 10.0, 20.0, 30.0,40.0,100.0] |
そして、流入速度ごとに計算を実行させます。
|
1 2 3 4 5 6 7 8 |
# 計算実行 for newU in newU_list: newCase = clone_file(orgCase, resultDir) new_parameter(newU, newCase) Allrun(newCase) print('='*50) |
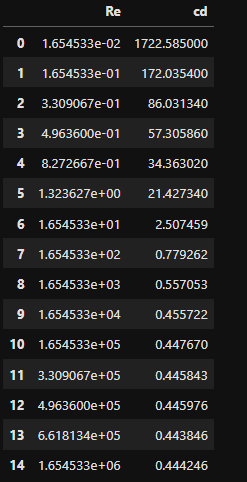
計算が終わったらレイノルズ数と抗力係数のデータフレームを作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from natsort import natsorted newCase_list = natsorted (os.listdir(resultDir) ) cd_list = [] Re_list = [] for i, newCase in enumerate(newCase_list): cd = cd_result(resultDir, newCase) Re = cd_Re(newU_list[i], cd) cd_list.append(cd[-1]) Re_list.append(Re) Re_ana, cd_ana = Cd_Re() df_cdRe = pd.DataFrame() df_cdRe['Re'] = Re_list df_cdRe['cd'] = cd_list df_cdRe |
実験データと今回の結果を比較します。
|
1 2 3 4 5 6 |
plt.scatter(np.log10(df_cdRe['Re']), np.log10(df_cdRe['cd']), color='blue', label = 'CAE') plt.plot(np.log10(Re_ana), np.log10(cd_ana), color='black', label='Exp') plt.grid() plt.legend() plt.xlabel('log10(Re)',fontsize=16) plt.ylabel('log10(Cd)',fontsize=16) |
レイノルズ数の広範囲で実験データと一致していますが、高いレイノルズ数で抗力係数が極端に落ちる部分は再現ができていません。今回、乱流モデルとしてRANSを選択しましたが、より渦の挙動をとらえるためLESなどの解析を試みたりする必要があり今後の課題ですね。
技術書
内容はブログ書いているOpenFOAMの内容を元に、対象を「2次元円柱内流れ」として、
- カルマン渦の生成
- レイノルズ数と抗力係数の関係
- レイノルズ数とストローハル数
- ポテンシャル流れと粘性流体の圧力係数の違い
- 力学的相似性
などなど、モデル作成からグラフ作成までの一連の流れをまとめたものになります。
ページ数は140ページです。
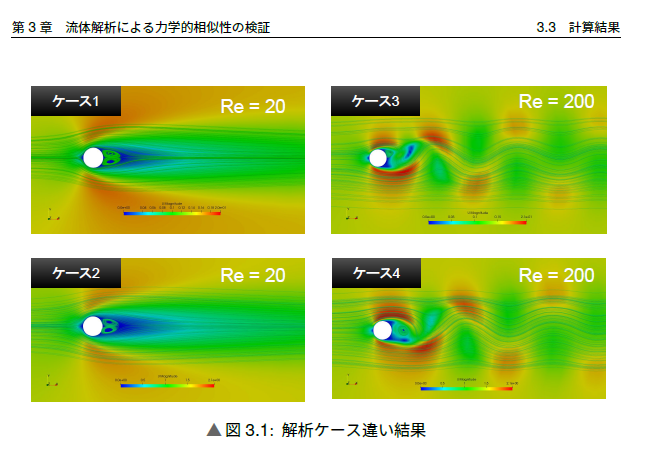

↓内容のチラ見せ
姉妹本として前回の技術書典16では、OpenFOAM(自宅で始める流体解析)の円管内流れについて触れいました。
参考書
PENGUINさんサイトを体系的に学べる書籍となっています。ネット記事でも十分勉強できるのですが、OpenFOAMの初学者でOpenFOAMをインストール済みであれば一冊持って置き、体系的に学ぶのが良いでしょう。
あとは初心者向けに丁寧に解説がされているこちらの書籍もお勧めです。最後の章にはオーバーセットメッシュ(重合メッシュ)の機能を使った解析を最後まで丁寧に解説しているので挫折することはないでしょう。





















直方体に一様流の風を当てて,迎角を変化させたときの抗力係数を調べたいです.