変数の一部を変換するラウシアンを考える意義

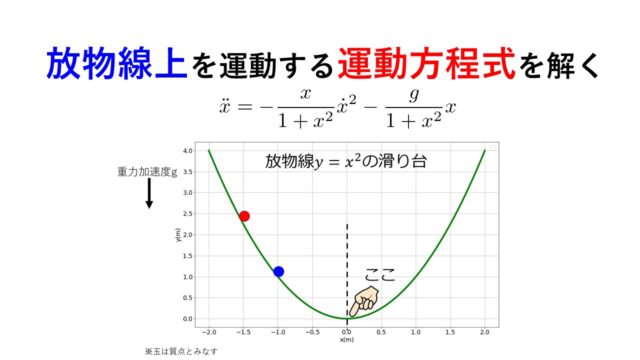
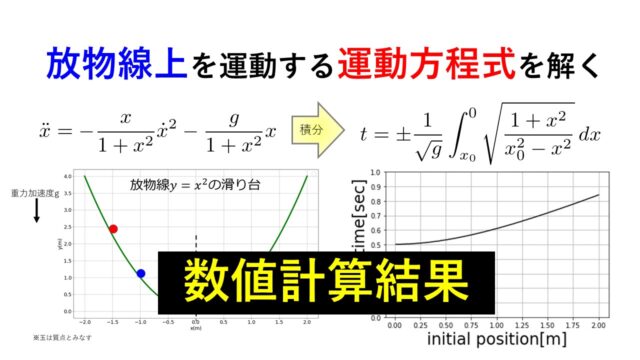
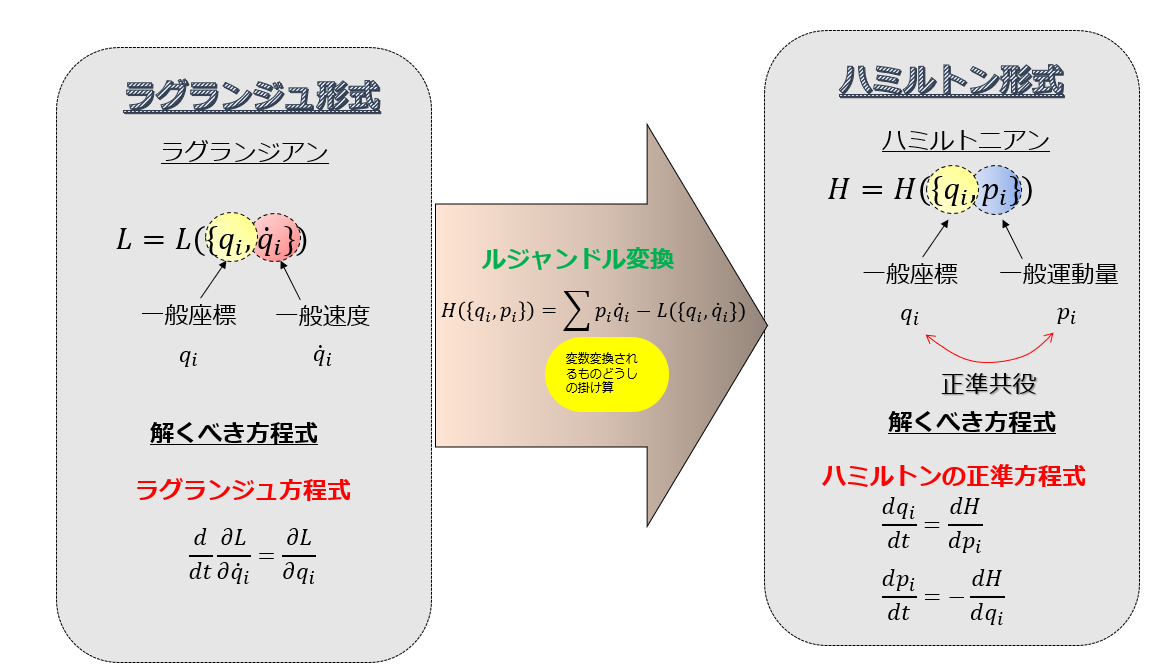
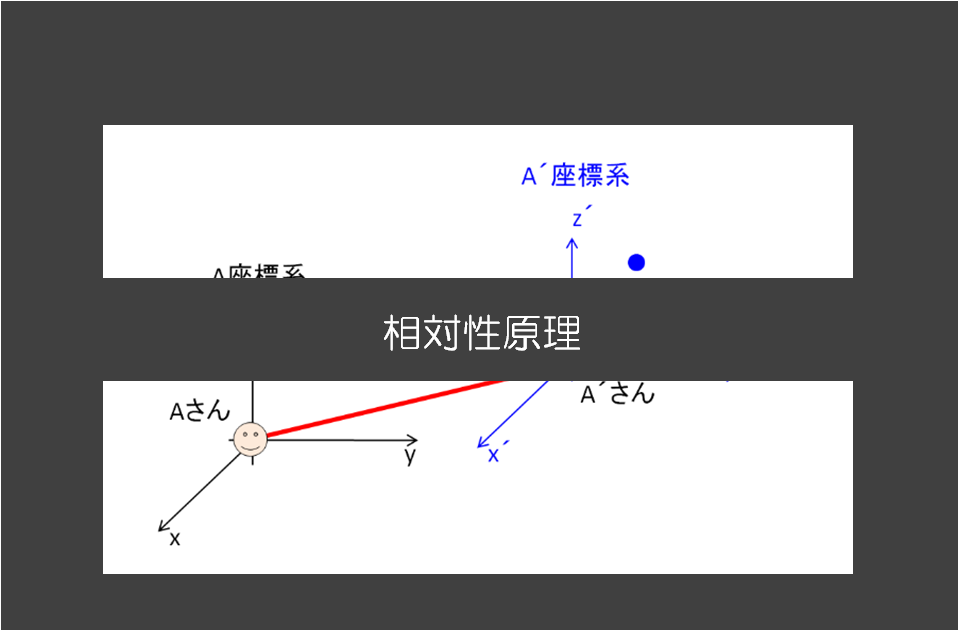
前回に、ラウシアンについて紹介しましたが、本日はラウシアンを考える意味について少しふれておこうと思います。

「ラウシアン」の記事はこちら

ラウシアンの概要説明
部分的に変換するこのラウシアンを導入すると何が嬉しいのか？
1. 循環座標
2. 循環座標の共役運動量は保存量
ラウシアンを導入することの嬉しさがようやく見えてきた
全体の流れ
全体の意味
思い・・・

ラウシアンの概要説明

変数である一般速度\(\dot{q}_{1},\dot{q}_{2},・・・,\dot{q}_{i},・・・,\dot{q}_{m},\dot{\xi}_{1},\dot{\xi}_{2},・・・,\dot{\xi}_{j},・・・,\dot{\xi}_{n}\)とあったときに、\(\{\dot{q}_{i}\}\)については一般運動量\(\{p_{i}\}\)に変換しますが、

一般速度\(\{\dot{\xi}_{j}\}\)については一般速度\(\{\dot{\xi}_{j}\}\)のままにしておくということを意味しています。

このようにした方が便利な場合もあるのです。

ラグランジアン		ラウシアン
\(L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\)		\(R(\{q_{i}\},\{\xi_{i}\},\{p_{i}\}\{\dot{\xi}_{i}\})\)
ラグランジュ方程式 \(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial q_{i}}\) \(\frac{d}{dt}\frac{\partial L}{\partial \dot{\xi}_{j}}=\frac{\partial L}{\partial \xi_{j}}\)	⇒ 一般速度\(\{\dot{q}_{i}\}\)⇒一般運動量\(\{p_{i}\}\) 部分的に変数を変換！！ ※（\(i=1～m\)）\(m\)個の自由度	ハミルトニアンの正準方程式 \(\frac{dq_{i}}{dt}=\frac{\partial R}{\partial p_{i}}\)・・・② \(\frac{dp_{i}}{dt}=-\frac{\partial R}{\partial q_{i}}\)・・・③
	⇒ 一般速度\(\{\dot{\xi}_{j}\}\) 変数を変換しない！！ ※（\(j=1～n\)）\(n\)個の自由度	ラグランジュ方程式 \(\frac{d}{dt}\frac{\partial R}{\partial \dot{\xi}_{j}}=\frac{\partial R}{\partial \xi_{j}}\)・・・④

このときにラグランジア\(L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\)からラウシアンへ\(R(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\)の変換は、

\begin{align*}R(\{q_{i}\},\{\xi_{i}\},\{p_{i}\}\{\dot{\xi}_{i}\})=\sum_{i}p_{i}\dot{q}_{i}-L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\cdot\cdot\cdot (5)\end{align*}

です。

変数を変換したいものだけ⑤のようにルジャンドル変換をすれば良いのですね。

部分的に変換するこのラウシアンを導入すると何が嬉しいのか？

ラウシアンを利用するのには、

いや、もっと広い意味ではハミルトンの正準方程式を考える意味は、むしろ循環座標が存在するときに最も効力を発揮します。

循環座標

その前に循環座標って何でしょうかね？(笑)

一般的にはラグランジアン\(L\)がある座標の変数を陽に含まないとき、その座標を循環座標と言います。

具体例を挙げますと、

中心力が存在する場合なんてのがその例でしょうか。

\begin{align*}L=T-U=\frac{m}{2}(\dot{r}^2+r^2\dot{\theta}^2)-U(r)\cdot\cdot\cdot (6)\end{align*}

ラグランジアン\(L\)の変数を書くと、\(L(r,\theta,\dot{r},\dot{\theta})\)と書きたいところですが、(6)式には\(\theta\)がありません。

ですので、\(L(r,\dot{r},\dot{\theta})\)となります。

このとき、\(\theta\)を循環座標と言います。

循環座標の共役運動量は保存量

循環座標であることがラウシアンを導入することの嬉しさは際立たせるのです。

\(\theta\)や\(\dot{\theta}\)に関する基礎式としては、

ラグランジュ方程式

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}}=\frac{\partial L}{\partial \theta}\cdot\cdot\cdot (7)\end{align*}

ですが、ラグランジアン\(L\)が\(\theta\)に依存していないので、⑦式の右辺は0ですよね。

つまり、

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}}=0\cdot\cdot\cdot (8)\end{align*}

となります。

\(\theta\)の共役運動量が

\begin{align*}p_{\theta}=\frac{\partial L}{\partial \dot{\theta}}\cdot\cdot\cdot (9)\end{align*}

前回の記事はこちら

運動量保存則：並進対称（ネーターの定理）：ランダウ=リフシッツの”力学”

であることを思い出すと、

(9)式より、

\begin{align*}\frac{d}{dt}p_{\theta}=0\end{align*}

⇔

\begin{align*}p_{\theta}=\alpha(=const)\cdot\cdot\cdot (10)\end{align*}

↑循環座標である\(\theta\)の共役運動量は保存量なのです。

その意味は何でしょうか？

保存量なら、変数として考える必要ないですよね(笑)

ということは、特別\(p_{\theta}\)を解くための方程式を用意する必要がないのです。

別の言い方をすると、系を記述するための自由度が減っています。

それはとても嬉しいことです。

自由度が多いということは、それを解くための方程式も自由度の数だけ用意する必要があるため、

「そんな数の連立方程式を解けるかー！！」

となる場合が多いのですが、方程式の数が減るだけで問題はずっと解きやすくなるのです。

とても嬉しいのです(^^)

ラウシアンを導入することの嬉しさがようやく見えてきた

⑤式を今、扱っている問題で考えるならば、

変数である一般速度(\(\dot{r},\dot{\theta}\))とあったときに、\(\dot{\theta}\)については一般運動量\(p_{\theta}\)に変換しますが、一般速度\(\dot{r}\)については一般速度\(\dot{r}\)のままにしておきます。

ラウシアンを書くと、

\begin{align*}R(r,\theta,\dot{r},p_{\theta})=p_{\theta}\dot{\theta}-L(r,\theta,\dot{r},\dot{\theta})\cdot\cdot\cdot (11)\end{align*}

と、こんな感じです。

でも、ラグランジアン\(L\)が\(\theta\)に依存していないので、

\begin{align*}R(r,\dot{r},p_{\theta})=p_{\theta}\dot{\theta}-L(r,\dot{r},\dot{\theta})\cdot\cdot\cdot (12)\end{align*}

↑これを見ると、当たり前ですが、ラグランジアン\(L\)が\(\theta\)に依存しないということは、ラウシアン\(R\)も\(\theta\)に依存しないことになります。

そうすると、⑬式の\(p_{\theta}\)については、⑩式で定数として決まっているので、④式

\begin{align*}\frac{d}{dt}\frac{\partial R(r,\dot{r},p_{\theta})}{\partial \dot{r}}=\frac{\partial R(r,\dot{r},p_{\theta})}{\partial r}\cdot\cdot\cdot (13)\end{align*}

を使えば、単に\(r\)とその微分\(\dot{r}\)について解くだけということになります。

\(r\)について⑬式より解くことができれば、②式より

\begin{align*}\frac{d\theta}{dt}=\frac{\partial R}{\partial p_{\theta}}\cdot\cdot\cdot (14)\end{align*}

を使って、\(\theta(t)\)が求まります。

全体の流れ

ラグランジアンを作る
\begin{align*}L=T-U=\frac{m}{2}(\dot{r}^2+r^2\dot{\theta}^2)-U(r)\cdot\cdot\cdot (6)\end{align*}

※変数である一般速度(\(\dot{r},\dot{\theta}\))とあったときに、\(\dot{\theta}\)については一般運動量\(p_{\theta}\)に変換しますが、一般速度\(\dot{r}\)については一般速度\(\dot{r}\)のままにしておきます。
循環座標：\(\theta\)
※循環座標とはラグランジアンに陽に含まれない変数のこと。

循環座標の一般運動量を計算
\begin{align*}p_{\theta}=\frac{\partial L}{\partial \dot{\theta}}\cdot\cdot\cdot (9)\end{align*}
運動量保存則：並進対称（ネーターの定理）：ランダウ=リフシッツの”力学”
\begin{align*}p_{\theta}=\alpha(=const)\cdot\cdot\cdot (10)\end{align*}

ラウシアンを作る
\begin{align*}R(r,\dot{r},p_{\theta})=p_{\theta}\dot{\theta}-L(r,\dot{r},\dot{\theta})\cdot\cdot\cdot (12)\end{align*}

\(r\)を求める
\begin{align*}\frac{d}{dt}\frac{\partial R(r,\dot{r},p_{\theta})}{\partial \dot{r}}=\frac{\partial R(r,\dot{r},p_{\theta})}{\partial r}\cdot\cdot\cdot (13)\end{align*}

を解くと、\(r(t)\)が求まる。

\(\theta\)を求める
\begin{align*}\frac{d\theta}{dt}=\frac{\partial R}{\partial p_{\theta}}\cdot\cdot\cdot (14)\end{align*}

を使って、\(\theta(t)\)が求まる。