こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本記事では、「相加変数、示量変数、示強変数」についてのお話をしたいと思います。
熱力学を勉強していると、熱力学的な平衡状態にあるときの系の状態は、互いに独立は状態量の組(状態変数)によって決まっているという書き方をされている解説が多いです。
熱力学的な状態量は例えば「圧力、温度、体積、エントロピー」などがありますね。
そもそも・・・
ってなっているかもしれません。
というわけで・・・・
- 相加変数、示量変数、示強変数をなぜ区別するのか?
- 示量変数、示強変数、相加性の違いは?
この記事を読み終わる頃には「示量変数、示強変数、相加性」が区別できて、明確に違いを認識した上で熱力学を学習できるはずです。
熱力学的な状態量は「示量性」か「示強性」の2種類に分けられる
熱力学的な平衡状態にあるときの系の状態は、互いに独立は状態量の組(状態変数)で書けます。
熱力学的な状態ってどんな状態かという話ですよね・・・
熱力学的な状態とは「今、なんかあったかい感じ・・・・」みたいなふわっとしたものではなく、「温度は10℃!」「圧力は110kPa」「体積は20L」などビシッと熱力学で決められた量で表現できる状態のことを言います。
「温度は10℃!」「圧力は110kPa」「体積は20L」などが状態量です。
熱力学的な状態量には、様々な状態量というのが出てきます。
いっぱいあります。
日常で、馴染みのあるものとして「圧力、温度、体積」くらいではないでしょうか?
これらの状態量が互いに独立に変化するものではなく、状態量には一定の関係性というのがあります。(追々、熱力学の記事を書きながら紹介していきます)。
均一で単成分な物質を例にとると、独立に変化する状態量は2つだけなので、状態量を2つ決めてしまえば残りの状態量は全て定まってしまいます(後半に事例を紹介します)。
だから熱力学を勉強したであれば、あまり深く考えず(多成分や不均一な系などは考えることがないので)、今考えている系に対してはどの2変数を使うと考えやすいかな?・・・
によって使う変数をを考えて熱力学の勉強を進めておけば当分は十分だろうと思います。
ここで、本題に入っていくのですが、上に挙げた状態量は「示量性」「示強性」のどの性質を持っているかのでしょうか?
こちらの書籍にあるように、状態量の「示量性」「示強性」は熱力学では本質的な違いがあります。
熱を考えると示強変数である温度で熱力学の話を進める場合が多いのですが、それでは「3重点で破綻」します。
示強変数では3重点で状態が区別できず、示量変数では状態が区別できる。
熱力学は示量変数で話を進めるのが自然。
写真「清水熱力学」 pic.twitter.com/Obo2ACH9aH
— カマキリ🐲@物理ブログ書いている (@t_kun_kamakiri) 2020年3月12日
熱力学では「相加変数(示量変数)だけを基本的な変数」とする姿勢で話を進めるのが自然である・・・とされていますが、
詳しくは述べることができないですが、状態量の「示量性」「示強性」の区別くらいはしておきましょう・・・・というのが本記事の内容です。
相加変数
「示量性」「示強性」の前に、相加性についての話をします。
相加性というのは、マクロな物理量(適当な状態量を\(X\)とおく)が、複数の容器に分割された際の一つの部屋の物理量\(X_{i}\)が以下のように書ける場合のことを言います。
X=\sum_{i}X_{i}\tag{1}
\end{align*}
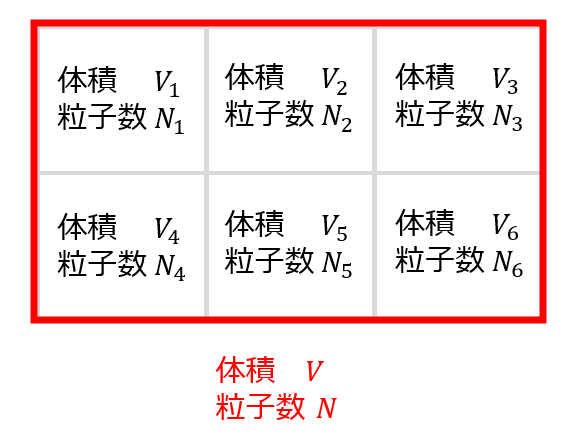


例えば、「体積\(V\)や物質量\(N\)」などは相加性があります。
V=V_{1}+V_{2}+V_{3}+V_{4}+V_{5}+V_{6}=\sum_{i}V_{i}\\
N=N_{1}+N_{2}+N_{3}+N_{4}+N_{5}+N_{6}=\sum_{i}N_{i}\tag{2}
\end{align*}
示量変数
任意の実数\(\lambda\)に対して、系全体を\(\lambda\)倍すると同じように\(\lambda\)倍される量を示量的と言います。
マクロな状態量\(X\)を「\(\lambda\)分の1」の部分系の状態量\(X_{i}\)との関係を考えます。
X=\lambda X_{i}\tag{3}
\end{align*}
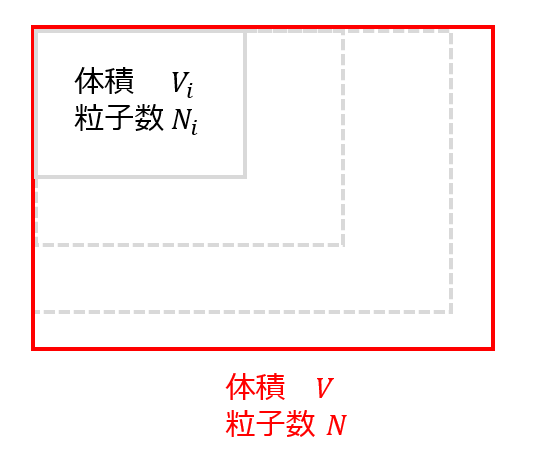


例えば、全体の体積\(V\)に対して部屋を\(\lambda\)分割した際の一つの部屋の体積\(V_{i}\)に対して以下が性質する場合、状態量は示量性があると言います。
V=\lambda V_{i}\tag{4}
\end{align*}
それは粒子数にも言えることです。
N=\lambda N_{i}\tag{5}
\end{align*}
この性質(示量性)を満たす状態量を示量変数と言います。
均一な系に対しては、相加性も示量性も区別が無くなります。
しかし、不均一の場合(例えば密度が空間的に一定ではない場合に)相加性が成立していても、示量性が成り立つとは限りません。
例えば、重力がかかっている場合には下の方が粒子数が多くなるので不均一になります。
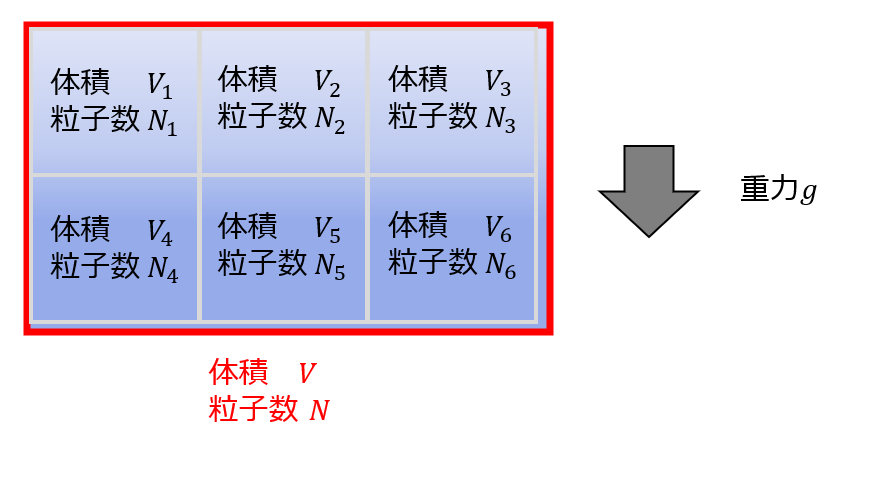

この時、物質量(粒子数)に対して相加性はあっても示量性となっているわけではありません。
熱力学のほとんどの内容は、均一の場合を扱うので「相加性と示量性」を区別して考えることが少ないですが、念のために相加性と示量性は違うということを認識しておきましょう。
示強変数
示量性(相加性)を持たない状態変数を示強変数といいます。
簡単に言ってしまえば、全体の体積\(V\)に対する状態量と部屋を\(\lambda\)分割した際の一つの部屋に対する状態量は同じであるという意味です。
示量変数と違って、示強変数は部分系(1ひとつの部屋)を定数倍したからといって系全体が定数倍されるわけではありません。
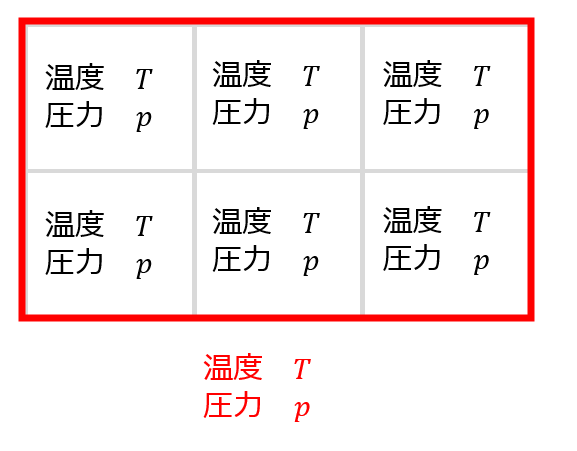


この性質(示強性)を満たす状態量を示強変数と言います。
温度\(T\)の容器を6分割したからって温度\(\frac{T}{6}\)になるわけではないですし、温度\(T_{1}\)の気体と温度\(T_{2}\)の気体を混ぜたからと言って、\(T_{1}+T_{2}\)になるわけではないです。
(エネルギーの次元)=(示量変数)×(示強変数)
示量変数と示強変数の中には、
(エネルギーの次元)=(示量変数)×(示強変数)\tag{6}
\end{align*}
となるものがあります。
例えば、
(仕事量)&=(体積)×(圧力)\\
(熱量)&=(エントロピー)×(温度)\\
(エネルギー)&=(物質量)×(化学ポテンシャル)\\\tag{7}
\end{align*}
こんな感じでです。
このような関係を(互いに)共役な関係または双対な関係と言います。
まとめ
【相加性】
X=\sum_{i}X_{i}\tag{1}
\end{align*}



X=\lambda X_{i}\tag{3}
\end{align*}



【示量変数の例】
体積\(V\)
エントロピー\(S\)
物質量\(n\)- 化学ポテンシャル\(\mu\)
エンタルピー\(H\)
内部エネルギー\(U\)
- 圧力\(p\)
- 温度\(T\)
- 化学ポテンシャル\(\mu\)
余談
均一で単成分な物質を例にとると、独立に変化する状態量は2つだけなので状態量を2つ決めてしまえば残りの状態量は全て定まってしまいます。
例えば、理想気体の状態方程式
pV=nRT\tag{8}
\end{align*}
を考えます。両辺を物質量\(n\)で割ります。
p\frac{V}{n}=RT\\
pv=RT
\end{align*}
となります。
体積\(V\)は示量変数なので、比体積として\(v=\frac{V}{n}\)とおきます。
そうすると変数は\(p,v,T\)の3つですが状態方程式という式が1つあるために、熱力学的な状態を定めようと思ったら3つの変数のうちのどれか2つが分かればよいというのがわかります。
このように熱力学では「圧力、温度、体積、内部エネルギー、エントロピー、エンタルピー」などいろいろな状態量が出てきますが、結局それらは互いに独立ではなく一定の関係性をもっているのです。
結局どの状態量を使うかは考えたい系によって使い分けるという事です。
ちなみに「熱量」と「仕事量」は状態量ではないので注意です(‘ω’)ノ