【置換：行列式の定義】3次の正方行列式を求めてみよう。

こんにちは(@t_kun_kamakiri)(^^)/

前回では、「サラスの公式を使って3次正方行列の行列式」の計算方法についての内容をまとめました。

前回の記事はこちら

【行列式の計算（サラスの公式）】3次正方行列は簡単。

3次までの行列式はサラスの公式通りで計算ができるのですが、
4次以上の正方行列の行列式はどのように計算するのでしょうか？

４次以上の正方行列については、から求めたりから求めたりします。今回は $n$ 次正方行列の行列式の定義から前回計算した3次の正方行列の行列式を計算してみましょう。

本記事の内容

行列式の定義( $n$ 次正方行列)
3次の正方行列の行列式の計算

※4次以上の正方行列に対する行列式の計算方法は次回の記事で解説を行います。

これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。

こんな人が対象

行列をはじめて習う高校生・大学生
仕事で行列を使うけど忘れてしまった社会人

この記事を読むと3次正方行列が簡単に求めることができるようになります(^^)/

行列式の定義
置換の定義
3次の行列式も行列式の置換を使って書いてみよう
1. サラスの公式(3次正方行列の行列式)
2. 行列の定義(3次正方行列の行列式)
まとめ
参考にする参考書はこれ

行列式の定義

まずは行列式の定義を書いておきましょう。
ちょっと何かいているのかわからないかもしれませんが後ほど詳しく解説します。

行列式の定義

$n$ 行 $n$ 列の正方行列Aについて、行列式を以下のように定義する。

$\begin{align*} |A|&=\sum sgn\, (\sigma) \cdot a_{1\sigma_{1}}a_{2\sigma_{2}}\cdots a_{n\sigma_{n}}\tag{1} \end{align*}$

このように定義できます。

$\sigma=\begin{pmatrix} 1 &2 &3 &\cdots &n \\ i_{1} &i_{2} &i_{3} &\cdots &i_{n} \end{pmatrix}$

$\sigma (1)=i_{1}$ , $\sigma (2)=i_{2}$ , $\cdots$

$n$ 次正方行列の行列式をシンプルに書くとめちゃくちゃ難しく感じますが、以下のポイントを押さえて順に理解していけばよいと思います。

$\sigma=\begin{pmatrix} 1 &2 &3 &\cdots &n \\ i_{1} &i_{2} &i_{3} &\cdots &i_{n} \end{pmatrix}\\$ とはどういう意味か？
3次の正方行列の行列式も(1)を使って出してみる。

まず $\sigma=\begin{pmatrix} 1 &2 &3 &\cdots &n \\ i_{1} &i_{2} &i_{3} &\cdots &i_{n} \end{pmatrix}\\$ がどういう意味かわからないので、(1)がどうなっているのか全く分かりませんよね。

置換の定義

まずは $\sigma=\begin{pmatrix} 1 &2 &3 &\cdots &n \\ i_{1} &i_{2} &i_{3} &\cdots &i_{n} \end{pmatrix}\\$ から解説します。

本記事では4次の正方行列の行列式を考えるため4文字の場合を考えてみます。

$\begin{align*} \sigma=\begin{pmatrix} 1 &2 &3 &4\\ i_{1} &i_{2} &i_{3}&i_{4}\end{pmatrix} \end{align*}$

置換に $sgn$ がsignatureの略が前についていますね。これが意味しているのはというものです。4文字なので入れ替えは $4!=24$ 通りあります。

具体的に書いてみると以下のようになります。

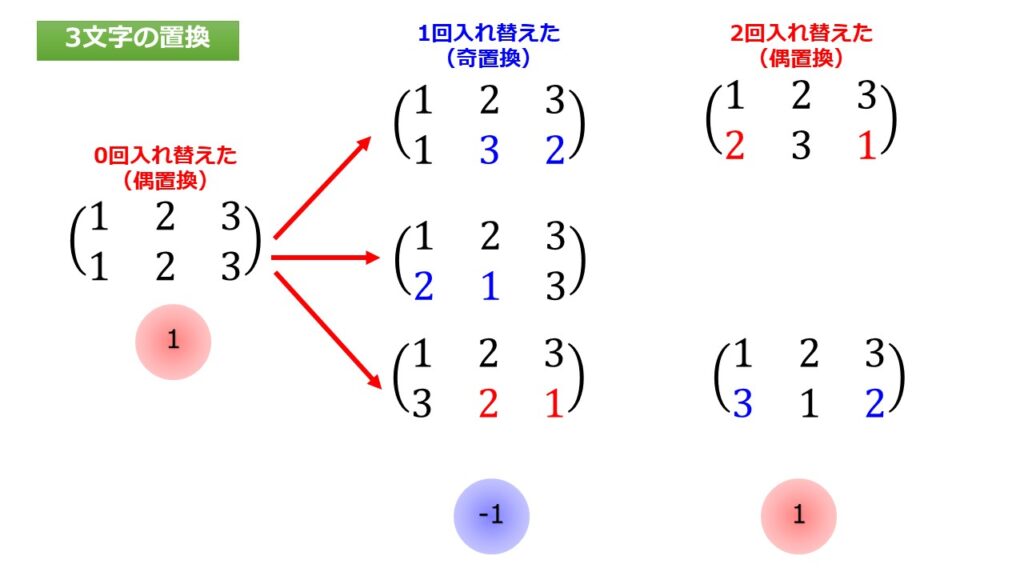
言葉にすると「下の行の数字の入れ替えた数」が、

偶数なら： $1$
奇数なら： $-1$

ということです。
だから結果は

$sgn\,\begin{pmatrix} 1 &2 &3 \\ 1 &2 &3\end{pmatrix}=1$
$sgn\,\begin{pmatrix} 1 &2 &3 \\ 1 &3 &2\end{pmatrix}=-1$
$sgn\,\begin{pmatrix} 1 &2 &3 \\ 2 &1 &3\end{pmatrix}=-1$
$sgn\,\begin{pmatrix} 1 &2 &3 \\ 3 &1 &2\end{pmatrix}=1$
$sgn\,\begin{pmatrix} 1 &2 &3 \\ 2 &3 &1\end{pmatrix}=1$
$sgn\,\begin{pmatrix} 1 &2 &3 \\ 3 &2 &1\end{pmatrix}=-1$

このようになります。

3次の行列式も行列式の置換を使って書いてみよう

3次正方行列 $A=\begin{pmatrix} a_{11} &a_{12} & a_{13} \\ a_{21} &a_{22} & a_{23} \\ a_{31} &a_{32} & a_{33} \end{pmatrix}\\$ の行列式を求めてみましょう。

前回の記事で「サラスの公式」を使って3次の正方行列の行列式を簡単に出しました。

前回の記事はこちら

【行列式の計算（サラスの公式）】3次正方行列は簡単。

ここでは、

サラスの公式
行列式の定義

以上の2つの方法から3次の正方行列の行列式を計算してみます。

サラスの公式(3次正方行列の行列式)

3次の正方行列の行列式の計算にはサラスの公式

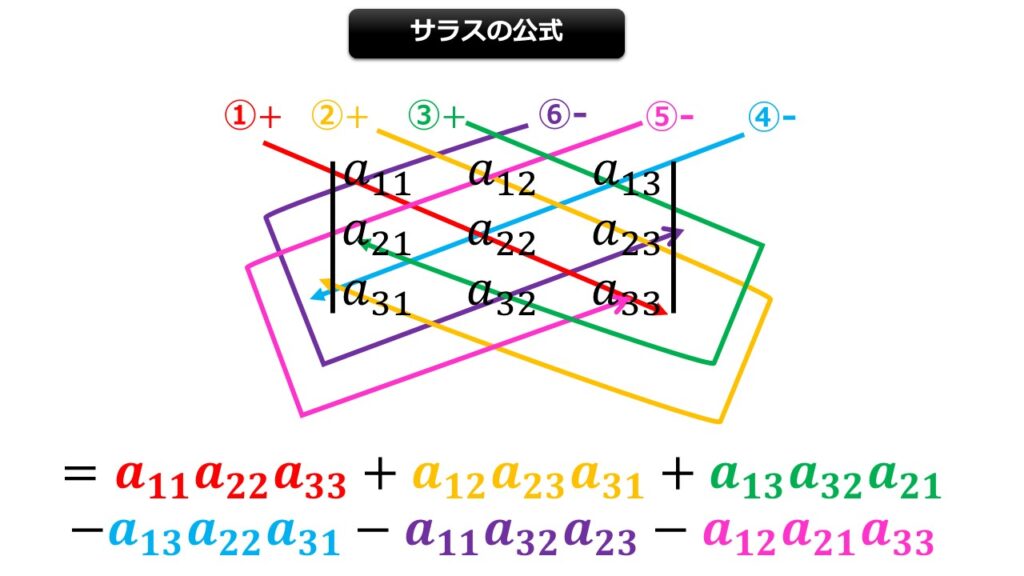
上の絵を見ながら計算を行えば3次正方行列に対しても行列式が計算できます。

$\begin{align*} |A|&=\begin{vmatrix} a_{11} &a_{12} & a_{13} \\ a_{21} &a_{22} & a_{23} \\ a_{31} &a_{32} & a_{33} \\ \end{vmatrix}\\ &=a_{11} a_{22} a_{33}+a_{12} a_{23}a_{31}+a_{13}a_{32}a_{21}\\ &-a_{13}a_{22} a_{31}-a_{11}a_{32} a_{23} -a_{13}a_{21}a_{33}\tag{2} \end{align*}$

行列の定義(3次正方行列の行列式)

既に結果はわかっているので本記事で書いた行列式の定義を使っても同じように行列式を導いてみましょう。

定義

$3$ 行 $3$ 列の正方行列Aについて、行列式を以下のように定義する。

$\begin{align*} |A|&=\sum sgn\, (\sigma) \cdot a_{1\sigma_{1}}a_{2\sigma_{2}}a_{3\sigma_{3}}\tag{3} \end{align*}$

$\sigma=\begin{pmatrix} 1 &2 &3 \\ i_{1} &i_{2} &i_{3} \end{pmatrix}\\$

まず(3)の和については $\sigma$ について $3!=6$ 通りの場合があったので、6個の和について計算をするという意味です。

$\begin{align*} |A|&=\sum sgn\, (\sigma)\cdot a_{1\sigma_{1}}a_{2\sigma_{2}}a_{3\sigma_{3}}\\ &=\underset{1}{sgn\,\begin{pmatrix} 1 &2 &3 \\ 1 &2 &3\end{pmatrix}}a_{11}a_{22}a_{33}+\underset{-1}{sgn\,\begin{pmatrix} 1 &2 &3 \\ 1 &3 &2\end{pmatrix}}a_{11}a_{23}a_{32}\\ &+\underset{-1}{sgn\,\begin{pmatrix} 1 &2 &3 \\ 2 &1 &3\end{pmatrix}}a_{12}a_{21}a_{33}+\underset{1}{sgn\,\begin{pmatrix} 1 &2 &3 \\ 2 &3 &1\end{pmatrix}}a_{12}a_{23}a_{31}\\ &+\underset{-1}{sgn\,\begin{pmatrix} 1 &2 &3 \\ 3 &2 &1\end{pmatrix}}a_{13}a_{22}a_{31}+\underset{1}{sgn\,\begin{pmatrix} 1 &2 &3 \\ 3 &1 &2\end{pmatrix}}a_{13}a_{21}a_{32}\\ &=a_{11} a_{22} a_{33}+a_{12} a_{23}a_{31}+a_{13}a_{32}a_{21}\\ &-a_{13}a_{22} a_{31}-a_{11}a_{32} a_{23} -a_{13}a_{21}a_{33}\tag{4} \end{align*}$

このように計算できます。

行列式の定義に従えば $n$ 次の行列式も計算できそうですね(^^)

まとめ

$A=\begin{pmatrix} a_{11} &a_{12} & a_{13} \\ a_{21} &a_{22} & a_{23} \\ a_{31} &a_{32} & a_{33} \end{pmatrix}\\$ の行列式を行列式の定義に従って計算しました。

サラスの公式を使った方が圧倒的に簡単ですが今回は行列式の定義に従って行列式を計算しました。3次の正方行列の行列式はまだサラスの公式があるのですが、4次正方行列の行列式を計算となると公式がないためどうやって計算すればよいのかわからない方も多いかと思います。今回のように行列式の定義に従って計算すれば4次の正方行列の行列式も計算ができるはずですね。

次回の行列式の定義を用いて4次正方行列の行列式の計算もやってみます！

前回の記事はこちら

【置換：行列式の定義】4次の正方行列式を求めてみよう。

参考にする参考書はこれ

当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。

基礎数学1線型代数入門

齋藤正彦

1,683円(03/29 08:11時点)

発売日: 2019/03/08

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

線形代数キャンパス・ゼミ　改訂8

馬場　敬之

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/

POSTED COMMENT

Jimmy より:

2022年11月3日 10:06

線形代数を再学習している60歳の男性です。とても参考にさせていただいております。
さて、線形代数(8)の講義の、置換の定義の中にある３文字の置換の図の、一回入れ替えた　と二回入れ替えた　のそれぞれの一番下の置換は、逆になっているのではないでしょうか？
つまり1→3,2→1,3→2の置換は二回入れ替えたもの、1→3,2→2,3→1の置換は一回入れ替えたもの
になるのではないでしょうか？
当方は全くの数字素人です。よって私の勘違いかもしれませんが、何か理由があるのかと素朴に疑問に思ったので、問い合わせさせていただきました。
よろしくお願いいたします。

ログインして返信する
- kamakiri より:
  
  2022年11月3日 23:24
  
  記事ご参考いただきありがとうございます。
  ご指摘ありがとうございます。
  ご指摘の通り誤記でした。
  こういった細かなミスは自分でも気づきにくい点ありますので、このようなご指摘は大変助かります。
  
  訂正しました。ご連絡いただきありがとうございました。
  
  ログインして返信する