解くべき方程式（2相流）
OpenFOAMの2相流のソルバ”interFoam”を用いて3次元ダムブレイクの解析を行います。
interFoamは気体と液体の気液混相流をVOF法で解くソルバーです。
ツール
- OpenFOAM:v2006
- ソルバ：inerFoam
解くべき方程式
- 運動方程式（2次元）
- 体積分率の保存
- 表面張力
※VOFによる界面の表現
今回使っている「interFoam」のソルバはVolume Of Fluid(VOF)法による、二相流ソルバーです。
相の区別を各相の体積分率(0~1)で行い、密度や粘性を体積分率をかけて、ナビエストークス方程式を解いています。
ナビエストークス方程式
\begin{align*}\frac{\partial \rho_{b}\boldsymbol{u}}{\partial t}+\nabla\cdot\big(\rho_{b}\boldsymbol{u}\boldsymbol{u}\big)=-\nabla p+\nabla\cdot\mu_{b}\big(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^{T}\big)+\rho_{b}\boldsymbol{f}+\boldsymbol{F}_{s}\end{align*}
密度
\begin{align*}\rho_{b}=\alpha_{1}\rho_{1}+\alpha_{2}\rho_{2}\end{align*}
粘性
\begin{align*}\mu_{b}=\alpha_{1}\mu_{1}+\alpha_{2}\mu_{2}\end{align*}
表面張力
\begin{align*}\boldsymbol{F}_{s}=\gamma \kappa\big(\nabla \alpha\big)\end{align*}
\begin{align*}\kappa=\nabla\cdot\big(\frac{\nabla\alpha}{|\nabla\alpha|}\big)\end{align*}
非圧縮の条件
\begin{align*}\nabla\cdot \boldsymbol{u}=0\end{align*}
体積分率の移流方程式
\begin{align*}\frac{\partial \alpha}{\partial t}+\nabla\cdot \big(\alpha \boldsymbol{u}\big)=0\end{align*}
※\(\alpha_{2}=1-\alpha_{2}\)
※\(\kappa\)：界面の曲率
※\(\gamma\)：界面張力
解析設定
水の領域設定
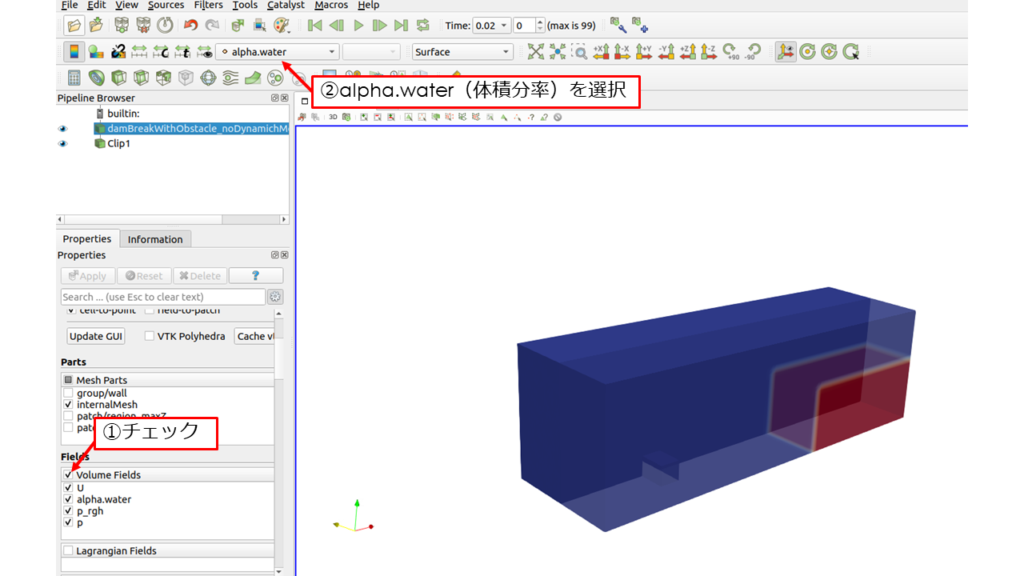
空気と水の領域をVOF法で設定する場合はsetFieldsDictによって設定を行います。
system/setFieldsDict
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object setFieldsDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // defaultFieldValues ( volScalarFieldValue alpha.water 0 volVectorFieldValue U (0 0 0) ); regions ( boxToCell { box (1.992 -1 0) (3.22 1 0.55); fieldValues ( volScalarFieldValue alpha.water 1 ); } ); // ************************************************************************* // |
setFieldsのオプションは以下があります。
- -case dir
Specify case directory to use (instead of cwd) - -decomposeParDict file
Use specified file for decomposePar dictionary - -dict file
Alternative setFieldsDict - -parallel
Run in parallel [Parallel option] - -region name
Specify alternative mesh region - -doc
Display documentation in browser - -help
Display short help and exit - -help-full
Display full help and exit
defaultFieldValuesでデフォルトの各相の体積分率と速度を設定することができます。
- volScalarFieldValue alpha.water 0
- volVectorFieldValue U (0 0 0)
boxToCellでどの領域にどのような設定を行うかを指定します。
- box (1.992 -1 0) (3.22 1 0.55)
- volScalarFieldValue alpha.water 1
boxはメッシュからはみ出た部分でもエラーは出ないので、境界ギリギリの寸法にせず大きめに設定しても良いです。
ではsetFieldsコマンドを実行して空気と水の体積分率を作成しましょう。
1 | setFields |
paraviewで結果を確認しましょう。
これで空気と水の初期状態ができました。
物性値の設定
system/transportProperties
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "constant"; object transportProperties; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // phases (water air); water { transportModel Newtonian; nu 1e-06; rho 1000; } air { transportModel Newtonian; nu 1.48e-05; rho 1; } sigma 0.07; // ************************************************************************* // |
ここでは水(water)と空気(air)の物性値を設定しています。
- transportModel：粘性項をニュートンの粘性法則（流れのせん断応力と流れの速度勾配が比例した粘性の性質を持つ流体と仮定）
- nu：動粘性係数[m2/s]
- rho：密度[kg/m3]
「sigma 0.07;」で表面張力$\kappa$の値を設定しています。
表面張力
- $\boldsymbol{F}_{s}=\gamma \kappa\big(\nabla \alpha\big)$
- $\kappa=\nabla\cdot\big(\frac{\nabla\alpha}{|\nabla\alpha|}\big)$
乱流モデル
今回は乱流モデル無しで行います。
constant/turbulenceProperties
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "constant"; object turbulenceProperties; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // simulationType laminar; // ************************************************************************* // |
今回こちら「$FOAM_TUTORIALS/multiphase/interFoam/laminar/damBreakWithObstacle/」のチュートリアルを利用していますが、乱流モデルなしのケースファイルでも「k,nut,omega」ファイルがありますが、こちらは乱流モデルの際に使うので今回は特に設定をしなくも良いです（使っていないので）。
0.org/U
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volVectorField; location "0"; object U; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 1 -1 0 0 0 0]; internalField uniform (0 0 0); boundaryField { region_maxZ { type pressureInletOutletVelocity; value uniform (0 0 0); } ".*" { type noSlip; } } // ************************************************************************* // |
重力の設定
constant/g
重力加速度はz方向の下向きに設定します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class uniformDimensionedVectorField; location "constant"; object g; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 1 -2 0 0 0 0]; value (0 0 -9.81); // ************************************************************************* // |
境界条件の設定
境界条件は、
- 速度$U$
- 圧力$p$
- 体積分率$\alpha$
の３つです。
0.org/U
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volVectorField; location "0"; object U; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 1 -1 0 0 0 0]; internalField uniform (0 0 0); boundaryField { region_maxZ { type pressureInletOutletVelocity; value uniform (0 0 0); } ".*" { type noSlip; } } // ************************************************************************* // |
0.org/p_rgh
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volScalarField; object p_rgh; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [1 -1 -2 0 0 0 0]; internalField uniform 0; boundaryField { ".*" { type fixedFluxPressure; phi phiAbs; value uniform 0; } region_maxZ { type totalPressure; p0 uniform 0; } } // ************************************************************************* // |
0.org/alpha.water
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object alpha.water; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 0 0 0 0 0 0]; internalField nonuniform List<scalar> boundaryField { region_maxZ { type inletOutlet; inletValue uniform 0; value uniform 0; } ".*" { type zeroGradient; } } |
境界条件についての考え方は自分もよくわからなくなるので、下記の記事で簡単にまとめておきました。特にマッハ数がいくつかによって境界条件の考え方が違ってくるので、整理しておく必要があります。
あわせて読みたい
スキームの設定
system/fvSchemes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object fvSchemes; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // ddtSchemes { default Euler; } gradSchemes { default Gauss linear; } divSchemes { div(rhoPhi,U) Gauss upwind; div(phi,alpha) Gauss vanLeer; div(phirb,alpha) Gauss linear; div(phi,k) Gauss upwind; div(phi,omega) Gauss upwind; div(((rho*nuEff)*dev2(T(grad(U))))) Gauss linear; } laplacianSchemes { default Gauss linear corrected; } interpolationSchemes { default linear; } snGradSchemes { default corrected; } wallDist { method meshWave; } // ************************************************************************* // |
system/fvSolution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object fvSolution; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // solvers { "alpha.water.*" { nAlphaCorr 1; nAlphaSubCycles 3; cAlpha 1; } p_rgh { solver GAMG; tolerance 1e-08; relTol 0.01; smoother DIC; cacheAgglomeration no; } p_rghFinal { $p_rgh; relTol 0; } "pcorr.*" { $p_rghFinal; tolerance 0.0001; } U { solver smoothSolver; smoother GaussSeidel; tolerance 1e-06; relTol 0; nSweeps 1; } "(k|omega|B|nuTilda).*" { solver smoothSolver; smoother symGaussSeidel; tolerance 1e-08; relTol 0; } } PIMPLE { momentumPredictor no; nCorrectors 3; nNonOrthogonalCorrectors 0; pRefPoint (0.51 0.51 0.51); pRefValue 0; } // ************************************************************************* // |
計算制御の設定（圧力計測点、水面高さ）
圧力計側点の設定
system/probes
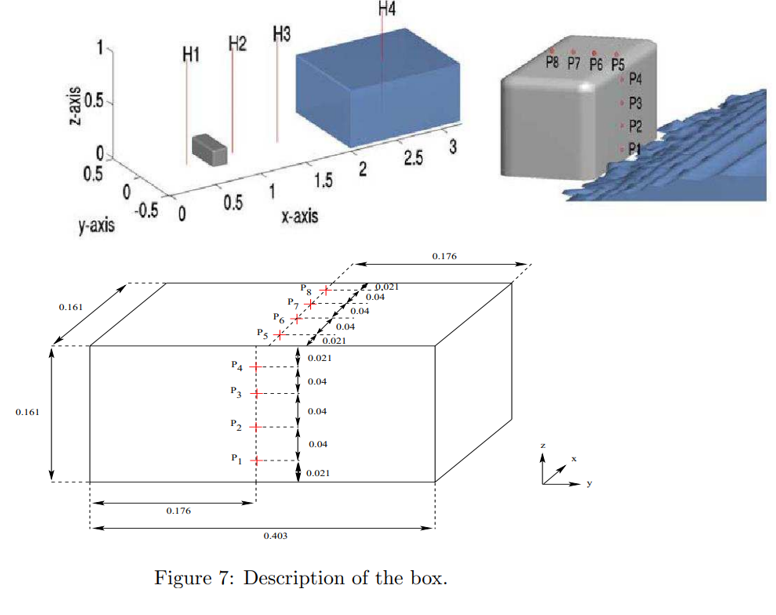
今回はこちらの実験データの圧力計測点と同じ位置の圧力データを取得する設定を行います。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | /*--------------------------------*- C++ -*----------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | Version: v2006 \\ / A nd | Website: www.openfoam.com \\/ M anipulation | ------------------------------------------------------------------------------- Description Writes out values of fields from cells nearest to specified locations. \*---------------------------------------------------------------------------*/ #includeEtc "caseDicts/postProcessing/probes/probes.cfg" //probes 設定の挿入 fields (p p_rgh); // プローブする場 probeLocations ( (0.8245001 0 0.0205) // プローブ座標 P1 (0.8245001 0 0.0605) // プローブ座標 P2 (0.8245001 0 0.1005) // プローブ座標 P3 (0.8245001 0 0.1405) // プローブ座標 P4 (0.8040 0 0.161 ) // プローブ座標 P5 (0.7640 0 0.161 ) // プローブ座標 P6 (0.7240 0 0.161 ) // プローブ座標 P7 (0.6840 0 0.161 ) // プローブ座標 P8 ); interpolationScheme cellPoint; // 補間スキーム // ************************************************************************* // |
- 「fields (p p_rgh);」で出力する物理量を指定します。
- probeLocationsで出力したい座標位置を指定します。
- 「interpolationScheme cellPoint」はセル値による線形重み付け補間スキーム
probesをsystem/controlDictで読み込みます。
水面高さの計測の設定
水面高さを計測するためinterfaceHeight1を設定します。
system/controlDict
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object controlDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // application interFoam; startFrom startTime; startTime 0; stopAt endTime; endTime 8; deltaT 0.001; writeControl adjustable; writeInterval 0.1; purgeWrite 0; writeFormat ascii; writePrecision 6; writeCompression off; timeFormat general; timePrecision 6; runTimeModifiable yes; adjustTimeStep yes; maxCo 0.5; maxAlphaCo 0.5; maxDeltaT 1; functions // 関数定義 { #includeFunc solverInfo(U,p,alpha.water); residuals { type solverInfo; libs ("libutilityFunctionObjects.so"); fields (".*"); } #includeFunc probes; // 壁面での圧力時系列モニター用のプローブ interfaceHeight1 { // Mandatory entries (unmodifiable) type interfaceHeight; //libs (“libfieldFunctionObjects.so”); libs (fieldFunctionObjects); // Mandatory entries (runtime modifiable) locations ( (0.496 0 0) (0.992 0 0) (1.488 0 0) (2.638 0 0) ); // Optional entries (runtime modifiable) alpha alpha.water; liquid true; direction (0 0 -1); interpolationScheme cellPoint; // Optional (inherited) entries writePrecision 8; writeToFile true; useUserTime true; region region0; enabled true; log true; timeStart 0; timeEnd 1000; executeControl timeStep; executeInterval 1; writeControl timeStep; writeInterval 1; } } // ************************************************************************* // |
「direction (0 0 -1);」は重力の方向を正しく指定する必要があります。
今回はz方向下向きに重力がはたらいているためこのような設定としました。
また、「postProcessing/interfaceHeight1/0/height.dat」には一つの座標に対して以下の出力結果が出されます。
- # hB : Interface height above the boundary：水面の高さ
- # hL : Interface height above the location：波の高さ
いずれも重力の方向を正しく指定することが重要です。
その他の設定
チュートリアルは空気と水の界面でのメッシュを時刻歴で再分割するようにdynamicMeshが採用されています。
今回このような設定では解析時間がとてもかかるのと、結果処理がものすごく重いためノートPCで耐えられる計算ではないため、「dynamicFvMesh staticFvMesh;」を使って無効にしておきます。
constant/dynamicFvMeshDict
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "constant"; object dynamicMeshDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dynamicFvMesh staticFvMesh; // |
decomposePar 並列計算の設定
計算時間もかかるため4並列にして計算を実行します。
system/decomposeParDict
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | /*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2006 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; object decomposeParDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // numberOfSubdomains 4; method scotch; // ************************************************************************* // |
scotchを使えば適当に最適化して分割してくれます。
以上で解析の設定が終わりました。
Follow @t_kun_kamakiri
大変貴重な記事ありがとうございます。