こんにちは(@t_kun_kamakiri)
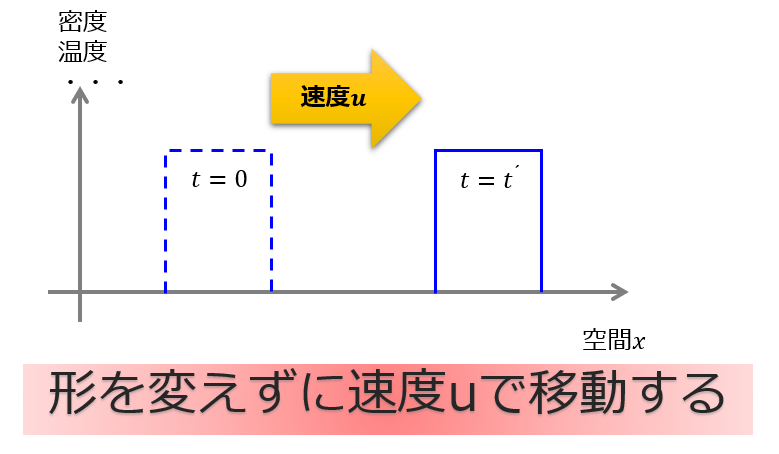
今回はOpenFOAMを使って移流方程式を解きたいと思います。その際に離散化スキームをどのように選択すると解の振る舞いが変わってくるのかを見ていきます。
OpenFOAMの移流方程式を使って中心差分と風上差分の結果比較を行います。
以前にも移流方程式を差分法を使ってFortranで解いたことがありますが、移流方程式は式が簡単で解析解があるにも関わらず数値的に解こうとすると、不安定だったり拡散してしまったり難しい問題があります。
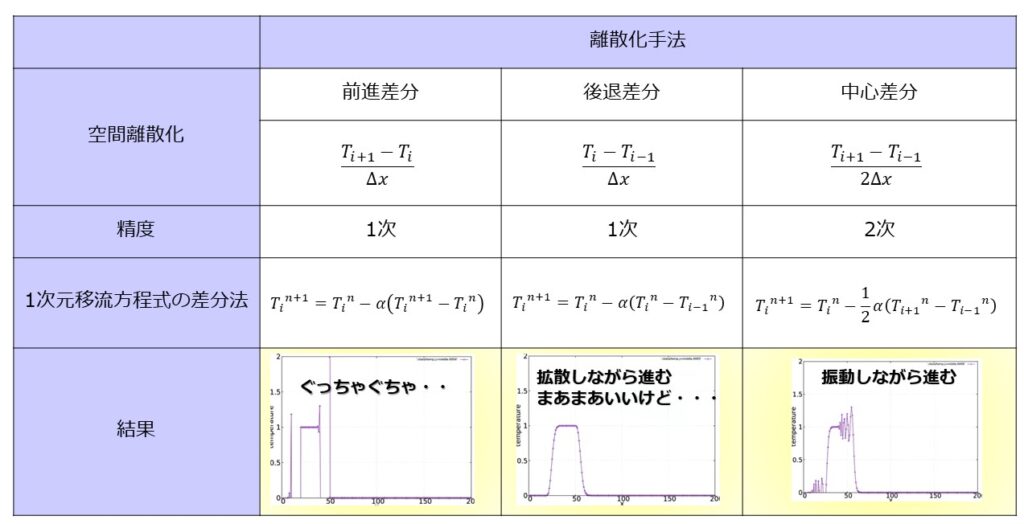
このように、流体の第二項の対流項$u\frac{\partial T}{\partial x}$の微分の離散化方法によっては、数値解が異なることがあります。異なると言っても、通常は流体のナビエストークスには流体粘性ので不連続解を分散させて解が振動しないようにしますし、不連続な解が出ることも稀なのでどのような離散化手法をとってもあまり解が変わりません。ただ、衝撃波が出ると速度や圧力の不連続解が生じ、さらに粘性項より対流項が大きくなるので上記に近い方程式になります。離散化スキームを以下のようにざっくり分けて特徴をまとめておきます。
- 1次精度:風上差分(upwind)→こちらは安定だが解が拡散してしまう
- 2次精度:中心差分、QUICK→こちらは不連続解をシャープにとらえようとするが、数値振動が起こりやすい
- TVDスキーム:minmod、vanLeer、vanAlbada、superBeeが有名。
色々な種類がありますが、不連続部分で振動を抑えるようにしながら、解はシャープにとらえようとするいい感じのスキーム
離散化スキームの種類はむちゃくちゃありますので、まずはこれくらいざっくりわけて特徴を理解しておくとよいでしょう。
- 対流項の発散スキームの比較
こちらはOpenFOAMの離散化スキームの比較として一番参考になる記事でしょう。 - Divergence scheme example
公式サイトにも離散化スキームに対する検討がされています。メッシュと離散化スキームの選択次第で結果がずいぶんと変わるのがわかるでしょう。 - OpenFOAM6.2 Numerical schemes
- OpenFOAM Basic Training
- 第1回オープンCAE講習会 OpenFOAM初中級講習B
- upwind_difference.pdf (xrea.com)
こちらのpdfはスキームについてよくまとめられています。
- OpenFOAMの移流方程式を使って離散化スキームの基礎的な内容を理解したい方
- OpenFOAMのチュートリアルから独自に検証するケースファイルを作りたい方
離散化スキームについて勉強したい方の参考になれば幸いです。
チュートリアルをコピーする
スカラー輸送方程式のチュートリアルをコピーします。
|
1 |
cp -r $FOAM_TUTORIALS/basic/scalarTransportFoam/pitzDaily 001_scalarTransportFoam |
「$FOAM_TUTORIALS」は環境変数で「/opt/OpenFOAM/OpenFOAM-v2012/tutorials」と割り当てられています(個人の環境に依る)。
ファイル構成は以下のようになっています。
|
1 2 3 4 5 6 7 8 9 10 11 |
. ├── 0 │ ├── T │ └── U ├── constant │ └── transportProperties └── system ├── blockMeshDict ├── controlDict ├── fvSchemes └── fvSolution |
scalarTransportFoamは以下の偏微分方程式を解く非定常のソルバーです。
\frac{\partial T}{\partial t}+\nabla\cdot(\boldsymbol{u}T)-\nabla\cdot (D_{T}\nabla T)=\boldsymbol{S}_{T}\tag{2}
\end{align*}
本記事では(2)を少し簡単にするために、
- 生成項を0:$\boldsymbol{S}_{T}=0$
- 拡散項を0:$D_{T}=0$
- 流速は一定:$\boldsymbol{u}=(0.1, 0, 0)$
と設定するようにします。
では、フォルダを移動します。
|
1 |
cd 001_scalarTransportFoam/ |
メッシュ生成
メッシュ生成はblockMeshを使います。
「system/blockMeshDict」ファイルを以下のように編集します。
system/blockMeshDict
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; object blockMeshDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // scale 1.0; xmax 1; ymax 0.1; zmax 0.1; vertices ( ( 0.0 0.0 0.0) ( $xmax 0.0 0.0) ( $xmax 0.0 $zmax) ( 0.0 0.0 $zmax) ( 0.0 $ymax 0.0) ( $xmax $ymax 0.0) ( $xmax $ymax $zmax) ( 0.0 $ymax $zmax) ); blocks ( hex (0 1 5 4 3 2 6 7) (100 1 1) simpleGrading (1 1 1) ); edges ( ); boundary ( XMin { type patch; faces ( (0 4 7 3) ); } XMax { type patch; faces ( (1 5 6 2) ); } ZMin { type empty; faces ( (0 1 5 4) ); } ZMax { type empty; faces ( (3 2 6 7) ); } YMin { type wall; faces ( (0 1 2 3) ); } YMax { type wall; faces ( (4 5 6 7) ); } ); mergePatchPairs ( ); // ************************************************************************* // |
以下のコマンドを実行してメッシュを作ります。
|
1 |
blockMesh |
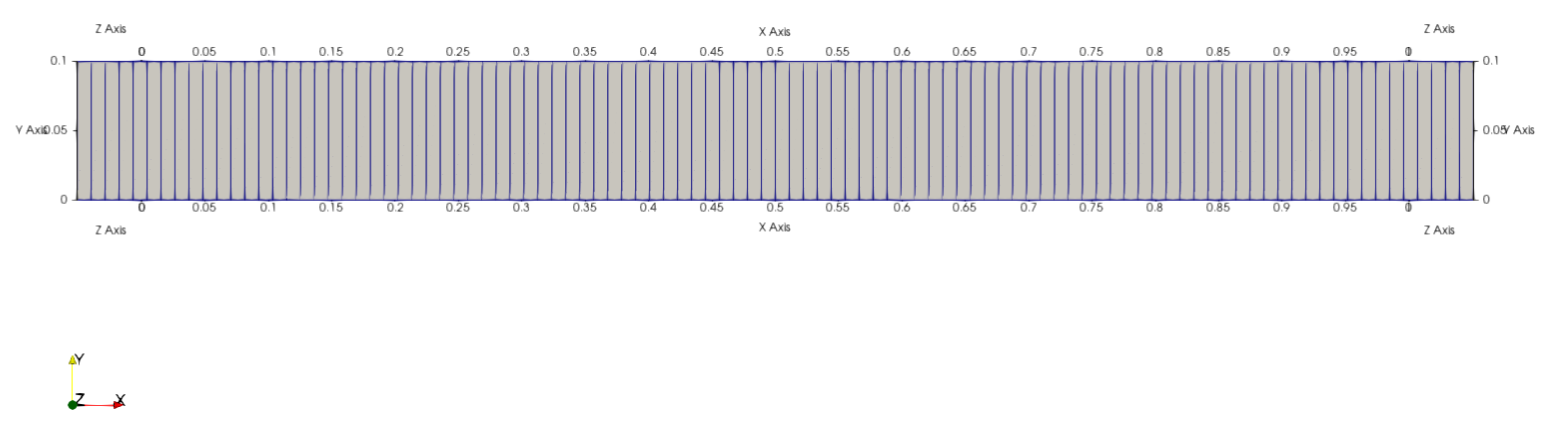
このように1.0×0.1×0.1の計算領域を作りました。
境界条件の設定
今回はxの正の方向へ流れが一様に0.1m/sで流れるようにします。
| U | T | |
| XMin |
type fixedValue;
value uniform (0.1 0 0);
or
type zeroGradient;
|
type zeroGradient; |
|
XMax
|
type zeroGradient;
|
type zeroGradient; |
|
YMin
|
type slip;
|
type slip;
|
|
YMax
|
type slip;
|
type slip;
|
|
ZMin
|
type empty;
|
type empty;
|
|
ZMax
|
type empty;
|
type empty;
|
Uがデフォルトでは既に速度の分布があるファイルになっているので、以下のように書き換えます。
0/U
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volVectorField; location "288"; object U; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 1 -1 0 0 0 0]; internalField uniform (0.1 0 0); boundaryField { XMin { type fixedValue; value uniform (0.1 0 0); } XMax { type zeroGradient; } YMin { type slip; } YMax { type slip; } ZMin { type empty; } ZMax { type empty; } } // ************************************************************************* // |
流速は一定:$\boldsymbol{u}=(0.1, 0, 0)$です。
これは時間が進行しても常に同じ値です。
次に温度境界条件を設定します。
0/T
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object T; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 0 0 1 0 0 0]; internalField uniform 0; boundaryField { XMin { type zeroGradient; } XMax { type zeroGradient; } ZMin { type empty; } ZMax { type empty; } YMin { type slip; } YMax { type slip; } } // ************************************************************************* // |
初期状態の設定
「setFields」で温度分布の初期条件を作ります。
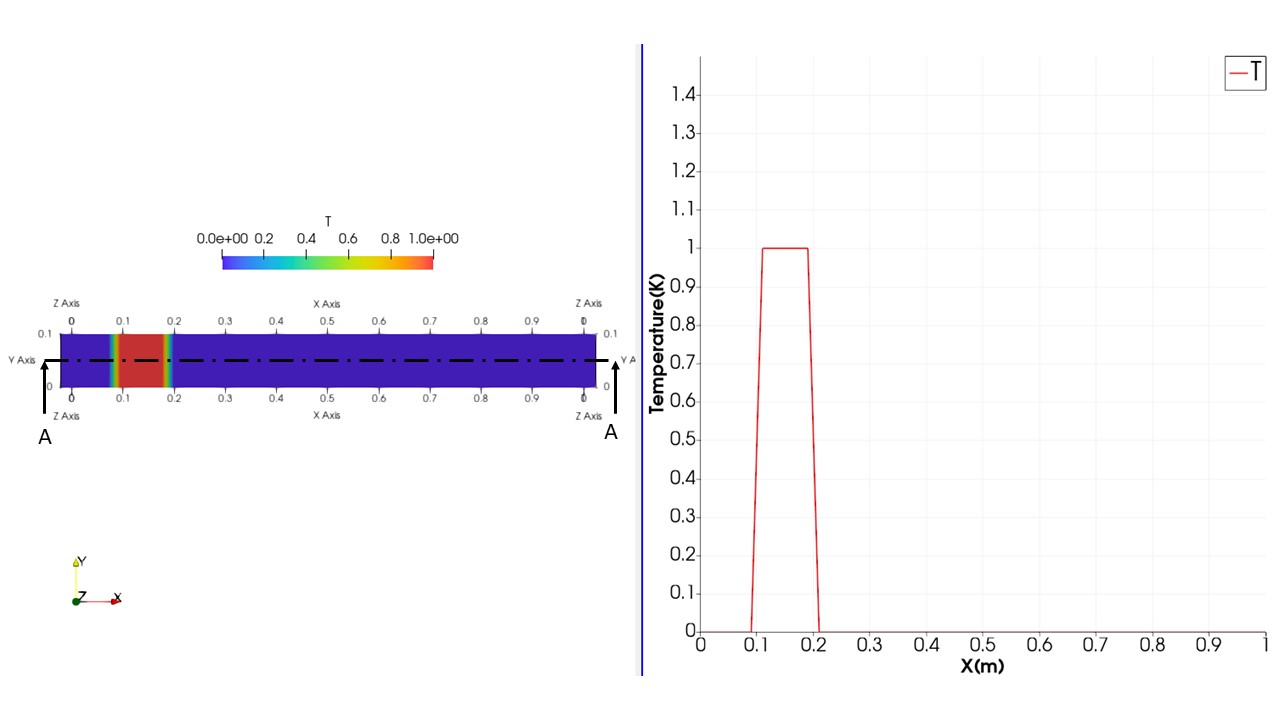

このように$x$方向0.1~0.2だけ$T=1$とし、その他を$T=0$となるように設定します。
設定ファイルはsetFieldsDictに書きますが、デフォルトではファイルが無いので適当なチュートリアルから持ってくる必要があります。
有名なのはinterFoamのdamBreakにsetFieldsDictがありますが、それを知らない場合は以下のコマンドでsetFieldsDictが使われているチュートリアルを探すことができます。
|
1 |
find $FOAM_TUTORIALS -name "setFieldsDict" |
コマンドを実行すると以下のようにずら~っと候補が出てきます。
|
1 2 3 4 5 6 7 |
/opt/OpenFOAM/OpenFOAM-v2012/tutorials/multiphase/compressibleInterDyMFoam/laminar/sphereDrop/system/setFieldsDict /opt/OpenFOAM/OpenFOAM-v2012/tutorials/multiphase/compressibleInterDyMFoam/laminar/sloshingTank2D/system/setFieldsDict /opt/OpenFOAM/OpenFOAM-v2012/tutorials/multiphase/driftFluxFoam/RAS/mixerVessel2D/system/setFieldsDict /opt/OpenFOAM/OpenFOAM-v2012/tutorials/multiphase/compressibleMultiphaseInterFoam/laminar/damBreak4phase/system/setFieldsDict /opt/OpenFOAM/OpenFOAM-v2012/tutorials/multiphase/twoLiquidMixingFoam/lockExchange/system/setFieldsDict /opt/OpenFOAM/OpenFOAM-v2012/tutorials/multiphase/interIsoFoam/damBreakWithObstacle/system/setFieldsDict (以下省略) |
適当に以下からコピーをしてきます。
|
1 |
cp -r /opt/OpenFOAM/OpenFOAM-v2012/tutorials/multiphase/compressibleInterDyMFoam/laminar/sphereDrop/system/setFieldsDict system/ |
以下のように編集します。
system/setFieldsDict
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object setFieldsDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // defaultFieldValues ( volScalarFieldValue T 0.0 //volVectorFieldValue U ( 0.1 0 0 ) ); regions ( boxToCell { box ( 0.1 -1 -1 ) ( 0.2 1 1 ); fieldValues ( volScalarFieldValue T 1 ); } ); // ************************************************************************* // |
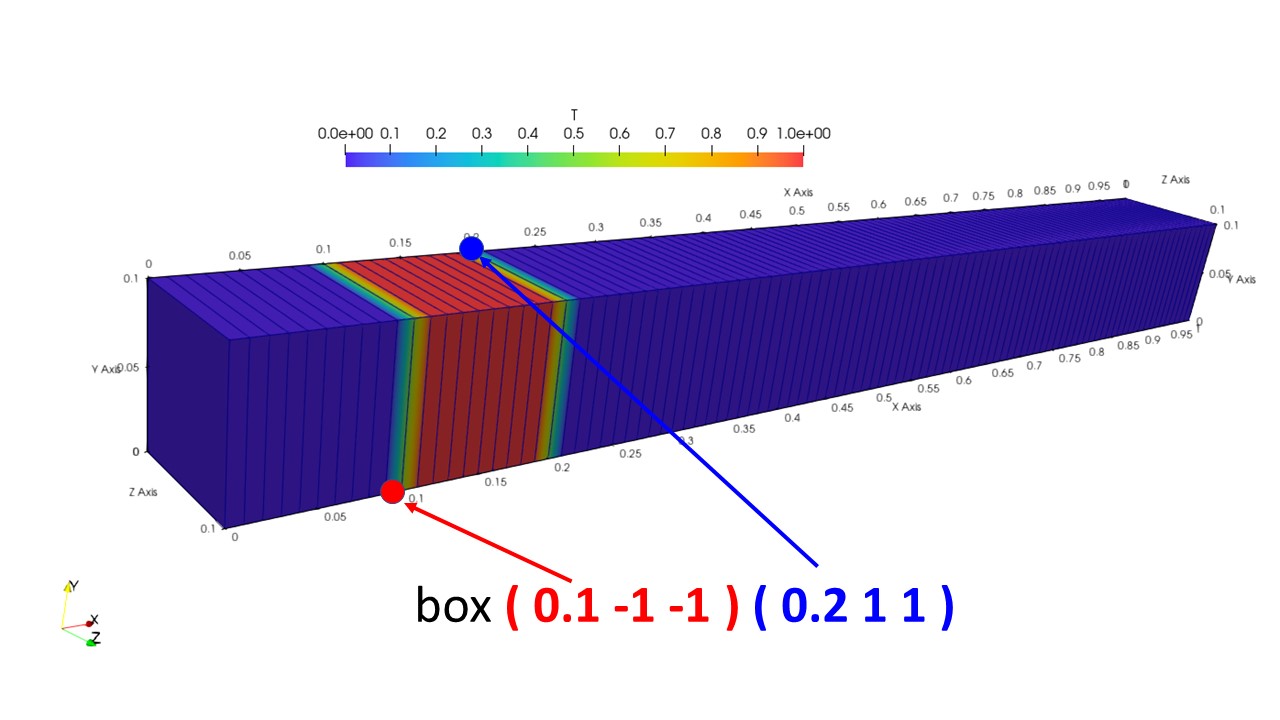
デフォルトは「volScalarFieldValue T 0.0」とし、「box ( 0.1 -1 -1 ) ( 0.2 1 1 );」の領域だけを「volScalarFieldValue T 1」という値にします。
では、以下のコマンドで初期状態を設定します。
|
1 |
setFields |
物性値の設定
今回は「拡散項を0:$D_{T}=0$」とします。物性値の設定は「constant/transportProperties」で行います。
constant/transportProperties
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "constant"; object transportProperties; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // DT 0.0; // ************************************************************************* // |
これにより、(2)のスカラー輸送方程式は移流方程式になります。
離散化スキームの設定
system/fvSchemes
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object fvSchemes; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // ddtSchemes { default Euler; } gradSchemes { default Gauss linear; } divSchemes { default none; // div(phi,T) Gauss linearUpwind grad(T); //線形風上差分 div(phi,T) Gauss linear grad(T); //中心差分 //div(phi,T) Gauss upwind grad(T); //風上差分 // div(phi,T) Gauss QUICK grad(T); //QUICK // div(phi,T) Gauss vanLeer grad(T); // div(phi,T) Gauss limitedLinear 0.1 grad(T); } laplacianSchemes { default none; laplacian(DT,T) Gauss linear corrected; } interpolationSchemes { default linear; } snGradSchemes { default corrected; } // ************************************************************************* // |
その他のスキームは別の記事で詳しく確認したいと思います。
計算制御の設定
解析時間や時間刻みは「system/controlDict」で設定を行います。
- 計算時間:5(秒)まで
- 時間刻み:0.001(秒)
system/controlDict
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object controlDict; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // application scalarTransportFoam; startFrom startTime; startTime 0; stopAt endTime; endTime 5; deltaT 0.001; writeControl timeStep; writeInterval 100; purgeWrite 0; writeFormat ascii; writePrecision 6; writeCompression off; timeFormat general; timePrecision 6; runTimeModifiable true; // ************************************************************************* // |
行列ソルバの設定
今回は特に設定を変えずにいきます。
system/fvSolution
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object fvSolution; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // solvers { T { solver PBiCGStab; preconditioner DILU; tolerance 1e-06; relTol 0; } } SIMPLE { nNonOrthogonalCorrectors 0; } // ************************************************************************* // |
解析実行(中心差分)
では計算を実行します。
|
1 |
scalarTransportFoam |
計算が終わったらParaViewで確認しましょう。
中心差分だと温度分布の形を保ったまま右へ進行するどころか、振動してとても不安定な結果になってしまいました。
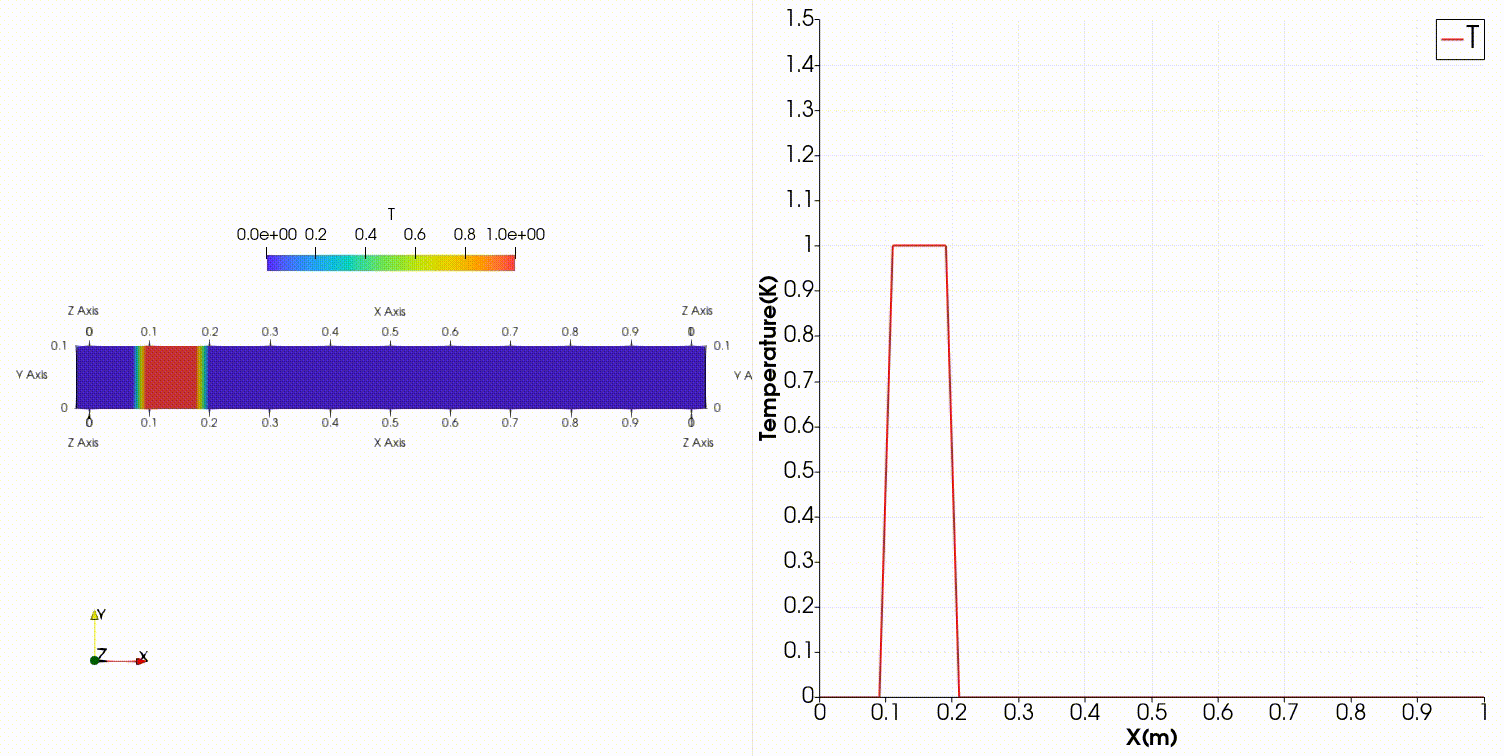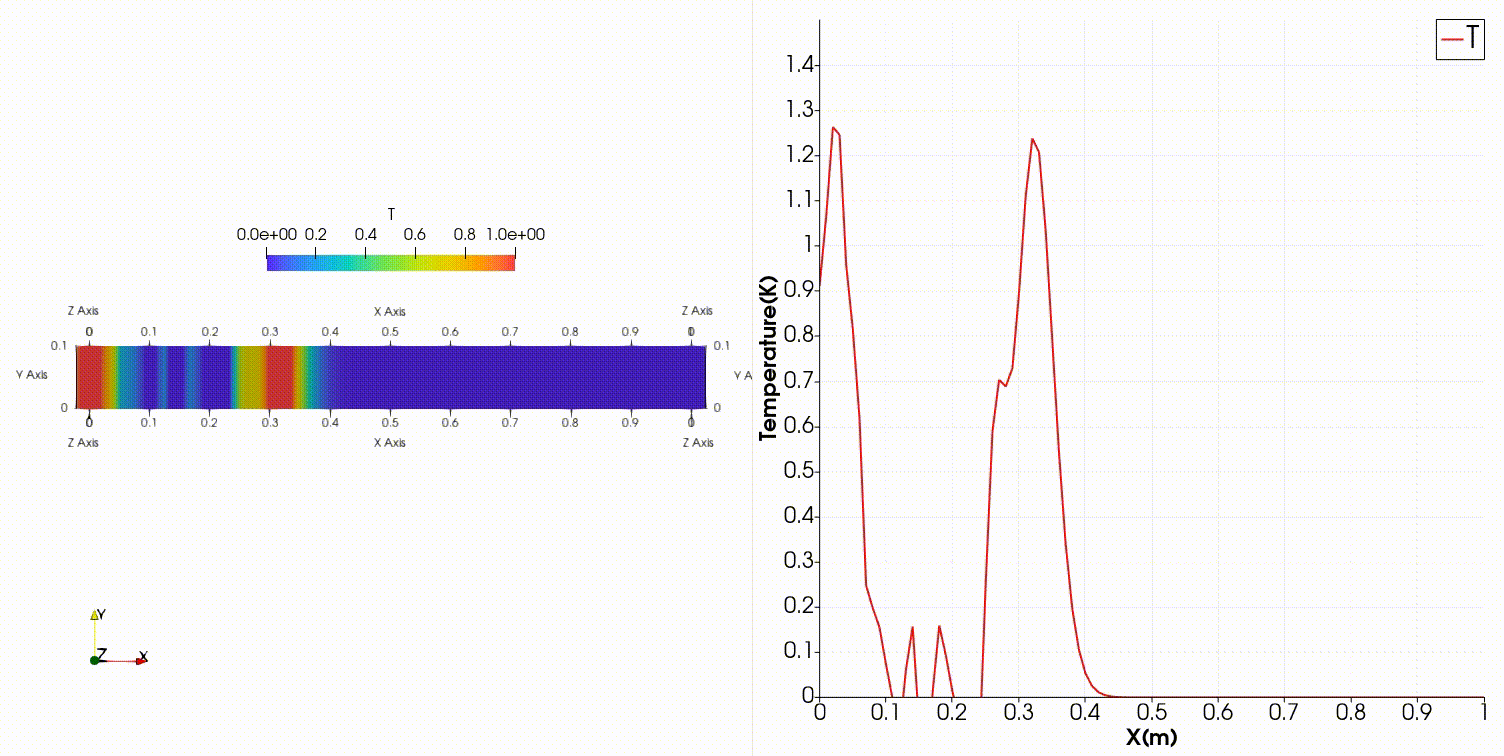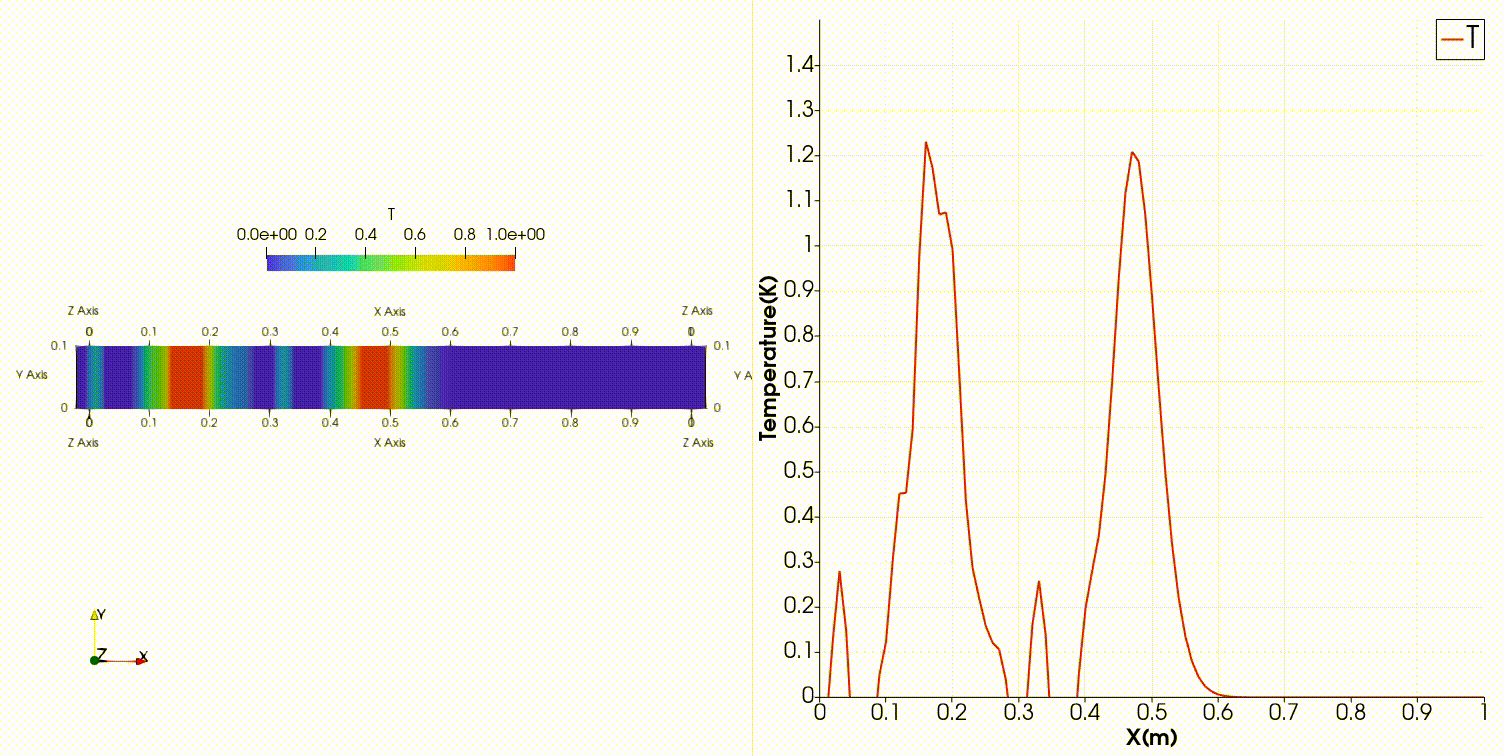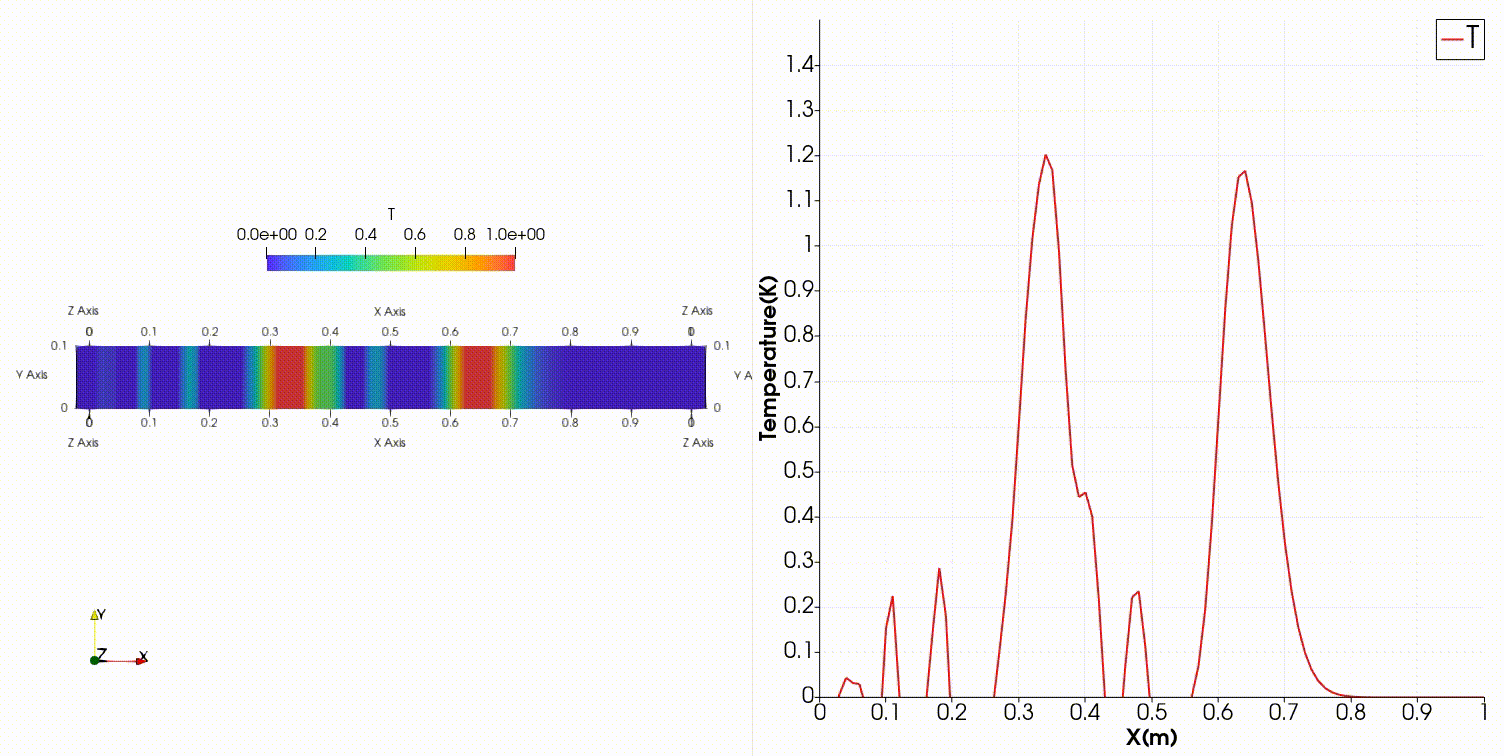

これはこちらの記事の内容と同じ結果になっていますね。
OpenFOAMは有限体積法でFortranでの結果は差分法ですが、移流項を中心差分で離散化するとどちらも振動する結果となっています。
ナビエストークス方程式には拡散項などがあるので振動も抑えられてしまいますが、発散項の中心差分での離散化は単独だと振動する解が出てきます。移流項を中心差分で解くと空間離散化の2次精度とは言え、振動する解となってしまうことは十分注意すべき点です。
解析実行(風上差分)
linear(中心差分で)は振動する解が得られたので今度は安定な差分法である風上差分を使います。以下「system/fvSchemes」でコメントアウトして風上差分を設定します。
system/fvSchemes
|
1 2 |
div(phi,T) Gauss upwind grad(T); //風上差分 // div(phi,T) Gauss linear grad(T); //中心差分 |
風上差分で拡散するやつ#移流方程式 pic.twitter.com/xFUtG5nKWR
— カマキリ🐲技術士勉強中 (@t_kun_kamakiri) February 1, 2023
Twitterにアップしたような拡散しながら右へ進行する解となりました。
こちらも記事の内容と同じ結果になっていますね。
まとめ
今回はスカラー輸送方程式のチュートリアルを変更して移流方程式にして、離散化スキームによる結果を見ました。
風上差分で拡散するやつ#移流方程式 pic.twitter.com/xFUtG5nKWR
— カマキリ🐲技術士勉強中 (@t_kun_kamakiri) February 1, 2023
微分を代数的に解くために離散化しているため、完ぺきな解法というものはなく一長一短ということですね。今回は中心差分と風上差分のみ紹介しましたが、その他に「線形風上差分」、「QUICK」、「TVD」など色々とあります。このようにスキームに対してどのような結果になるのかを知るためには離散化手法を知ることが大事ですが、何より計算で確かめてみることが良いでしょう。
有限体積法の「中心差分」による離散化はこちらにまとめています。1次元の熱拡散方程式ですが、参考になるでしょう。
次回はスキームを色々変えて結果の違いを確かめたいと思います。複数ケースの計算を行うためスキームを変えて計算するプログラムを作って計算します。
「対流項の発散スキームの比較」にシェルスクリプトで自動で計算するプログラムがあります。シェルスクリプトはちょっと慣れないのでPythonで行いたいと思います。
参考書
有限体積法の勉強にはこの本で間違いないです。
対流項目が中心差分で安定しないことを理論的に評価しておりとても参考になります。
OpenFOAMの基本的な設定を学ぶことができる書籍として以下の参考書がお勧めです。
本書はESI版ではなくFoundation版でありOpenFOAMv2.xで書かれたやや古い内容です。その点に注意してESI版のお使いのversionとの違いを丁寧に調べることができる方であれば、十分参考になる書籍です。
OpenFOAM全般の設定などまとめられた書籍として以下のものがあります。
こちらもFoundation版なので、ESI版のお使いのversionとの違いを丁寧に調べることができる方であれば、十分参考になる書籍です。
こちらのオープンCAE学会から技術書典にOpenFOAMでメッシュ作成【PDF版】が出ています。難しい内容ではありますが、OpenFOAMのメッシュに関する内容が1000円で学べます。