こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
前回の記事では球体周りの抗力係数を乱流域で再現できるかというのを検証しました。
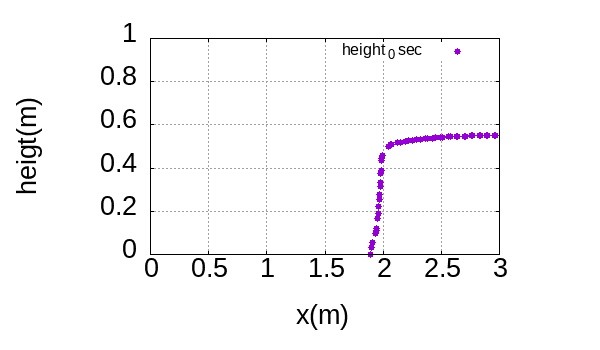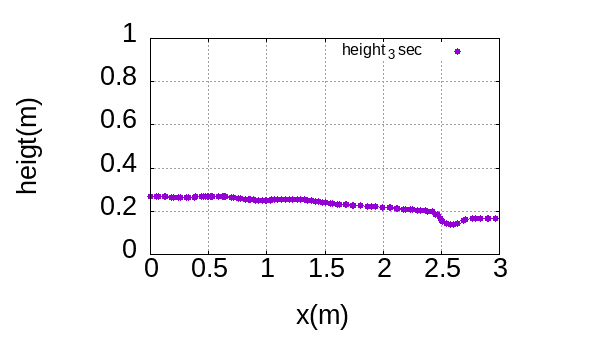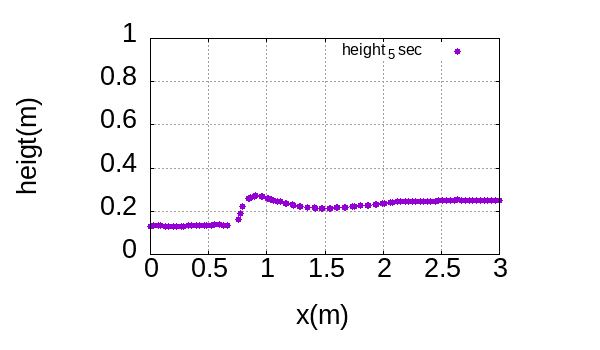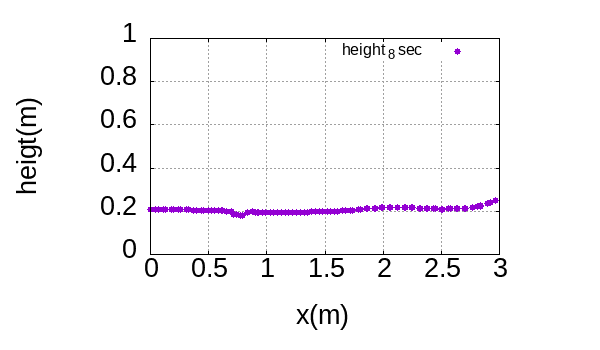
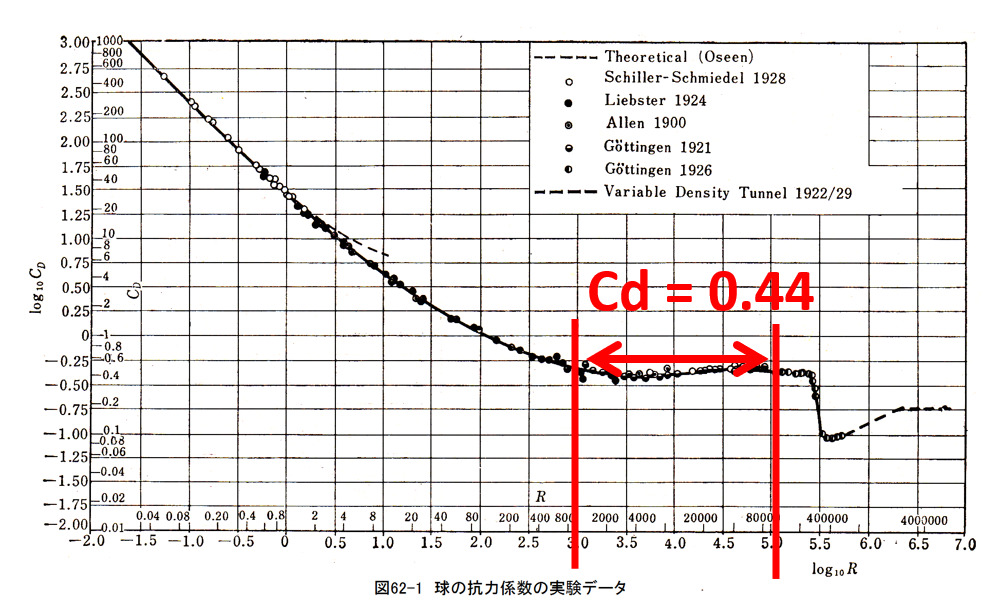
結果はレイノルズ数：$Re=\frac{Ud}{\nu}=\frac{1.0*0.128}{1.5e-5}=8,533$(乱流状態)での抗力係数0.44に対して、OpenFOAMでの結果も文献を再現する数値Cd=0.45でした。
今回興味があるのは球体表面によって抗力係数が変わるのかということです。
こちらの記事であるように、ゴルフボールは表面に窪みがいっぱいある状態（ディンプル）によってこうレイノルズ数での抗力係数が極端に落ち込む（ドラッグクライシス現象）位置を低レイノルズ数側へがシフトすることができます。
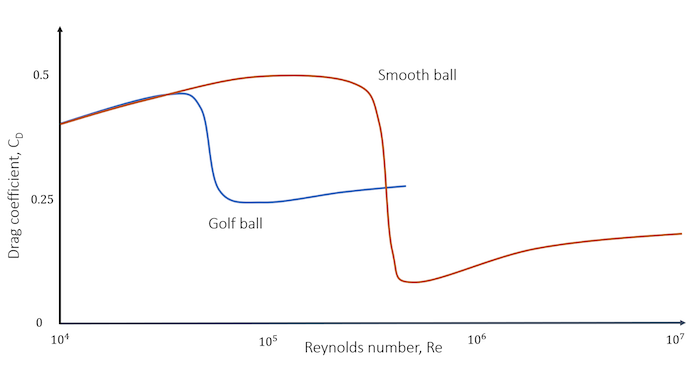
過去に球体周りの抗力係数が文献通りになるか検証しましたが、このドラッグクライシス現象のような挙動は再現できませんでした。
【OpenFOAM球体周りの抗力係数(5)】Pythonでパラメータスタディ
※こちらのメッシュ生成はsnappyHexMeshで行いました。
ドラッグクライシスを再現するには球体周りで相当数のメッシュ生成を行い、非定常で乱流モデルはLESなどを使い渦の剥離点を正確に再現することが求められると思われます。しかし、自宅PCスペック程度の自分の計算環境では到底無理なので諦めました_(._.)_
興味があるのはゴルフボールなど球体表面に工夫をすることで抗力係数がどれだけ変わるかということです。ゴルフボールの先行研究は多くあるので、バスケットボールならどうか？ということでバスケットボール周りの抗力係数を出してみたいと思います。
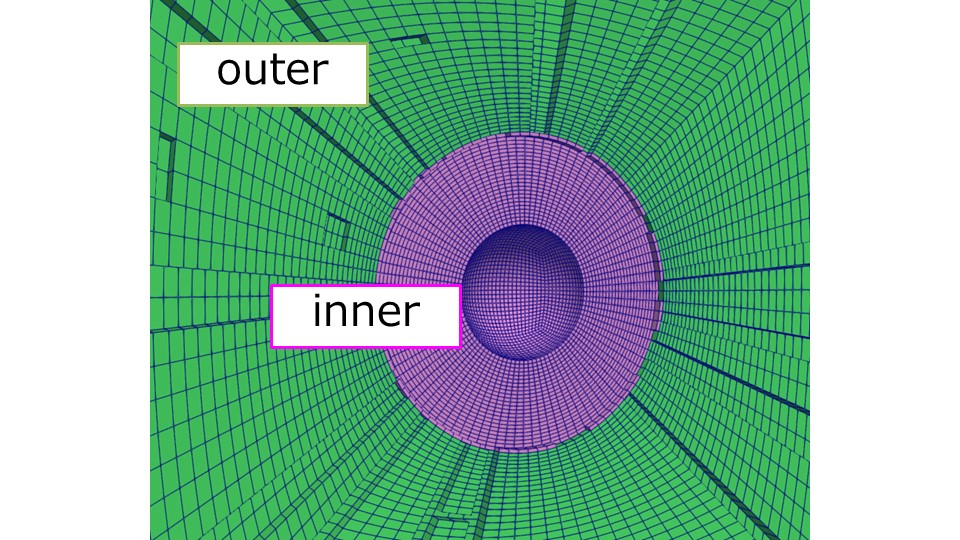
以前の記事では球体周りとその外側の領域を別々で作成しました。
球体まわりのメッシュをinnerとouterに分けて別々で6面体メッシュで生成しています。
InnerとouterをcyclicAMI周期境界でつないで球体まわりの解析を行う
今回はinner部分をバスケットボール形状にフィットするように変形して作成するという方法を取ります。
バスケットボール形状にフィットするようにdynamicMeshを利用する
参考にした記事はこちらです。
【OpenFOAM】ゴルフボールはどう打ったら最もよく飛ぶのか
※モデルを頂きブログ記事での解説のお許しを得たので皆さんに共有いたします。
記事内で「SALOMEを用いて下図のようなメッシュを作成しました。全てヘキサで作成した後にrefineMeshにて一部をポリヘドラに細分化」と書いてありますが、当ブログではゴルフボールではなくバスケットボールまわりのメッシュ作成をします。また、全てblockMeshのみで作成するので記事内の作り方と異なります。
バスケットボール形状
バスケットボール形状の形状はFreeCADで作成しました。
モデルの作成方法はこちらです。
実物のバスケットボールのサイズを調べる前に適当に作れるかどうかを試したものなので、作成したモデルはΦ400となっています。
後々調べるとバスケットボールは7号ボールでΦ250程度なので、Φ250になるようにstlをスケール変換します。
例えば以下のコマンドでスケール変換ができます。
1 | surfaceConvert -scale 0.625 constant/triSurface/basketball.stl constant/triSurface/basketball_m1.stl |
これでΦ400からΦ250のバスケットボールの形状にスケール変換できました。
dynamicMeshチュートリアルのコピー
dynamicMeshの使い方はこちらの記事がとても参考になりました。
しかし、現在のOpenFOAMのバージョン(v2212)とは少々使い方が異なるので、別途調べる必要があります。
適当なチュートリアルを持ってきます。
1 | cp -r /usr/lib/openfoam/openfoam2212/tutorials/mesh/moveDynamicMesh/SnakeRiverCanyon dynamicMesh_basketball |
innerのベースメッシュの変更
innerメッシュをouterメッシュをコピーしてきて以下のようにフォルダを分けておきます。
1 2 3 | -- 001_inner -- 002_outer -- sample //先ほどコピーしたdynamicMeshのチュートリアル（参考にするため） |
今回dynamicMeshでメッシュをバスケットボール形状にフィットさせるのはinnerのメッシュのみでouterは後ほどmergeするために同じフォルダに移しておきます。
バスケットボールの溝を再現するためにめしゃくちゃメッシュを細かくする必要がありました。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 | scale 1; verbose yes; // basketball r = 0.125m r_in 0.128; r_ami 0.148; r_out 0.5; n 256; v #calc "1.0/sqrt(3.0)"; a #calc "1.0/sqrt(2.0)"; v_in #calc "$r_in*$v"; mv_in #calc "-$v_in"; a_in #calc "$r_in*$a"; ma_in #calc "-$a_in"; v_ami #calc "$r_ami*$v"; mv_ami #calc "-$v_ami"; a_ami #calc "$r_ami*$a"; ma_ami #calc "-$a_ami"; a_out #calc "$r_out*$a"; ma_out #calc "-$a_out"; vertices ( ($mv_in $mv_in $mv_in) // 0 ( $v_in $mv_in $mv_in) // 1 ( $v_in $v_in $mv_in) // 2 ($mv_in $v_in $mv_in) // 3 ($mv_in $mv_in $v_in) // 4 ( $v_in $mv_in $v_in) // 5 ( $v_in $v_in $v_in) // 6 ($mv_in $v_in $v_in) // 7 ($mv_ami $mv_ami $mv_ami) // 8 ( $v_ami $mv_ami $mv_ami) // 9 ( $v_ami $v_ami $mv_ami) // 10 ($mv_ami $v_ami $mv_ami) // 11 ($mv_ami $mv_ami $v_ami) // 12 ( $v_ami $mv_ami $v_ami) // 13 ( $v_ami $v_ami $v_ami) // 14 ($mv_ami $v_ami $v_ami) // 15 ); blocks ( hex ( 9 8 12 13 1 0 4 5) ($n $n 10) simpleGrading (1 1 1) hex (10 9 13 14 2 1 5 6) ($n $n 10) simpleGrading (1 1 1) hex (11 10 14 15 3 2 6 7) ($n $n 10) simpleGrading (1 1 1) hex ( 8 11 15 12 0 3 7 4) ($n $n 10) simpleGrading (1 1 1) hex ( 8 9 10 11 0 1 2 3) ($n $n 10) simpleGrading (1 1 1) hex (13 12 15 14 5 4 7 6) ($n $n 10) simpleGrading (1 1 1) ); edges ( arc 8 9 (0 $ma_ami $ma_ami) // 0 arc 10 11 (0 $a_ami $ma_ami) arc 14 15 (0 $a_ami $a_ami) arc 12 13 (0 $ma_ami $a_ami) arc 8 11 ($ma_ami 0 $ma_ami) // 4 arc 9 10 ($a_ami 0 $ma_ami) arc 13 14 ($a_ami 0 $a_ami) arc 12 15 ($ma_ami 0 $a_ami) arc 8 12 ($ma_ami $ma_ami 0) // 8 arc 9 13 ($a_ami $ma_ami 0) arc 10 14 ($a_ami $a_ami 0) arc 11 15 ($ma_ami $a_ami 0) arc 0 1 (0 $ma_in $ma_in) // 12 arc 2 3 (0 $a_in $ma_in) arc 6 7 (0 $a_in $a_in) arc 4 5 (0 $ma_in $a_in) arc 0 3 ($ma_in 0 $ma_in) // 16 arc 1 2 ($a_in 0 $ma_in) arc 5 6 ($a_in 0 $a_in) arc 4 7 ($ma_in 0 $a_in) arc 0 4 ($ma_in $ma_in 0) // 20 arc 1 5 ($a_in $ma_in 0) arc 2 6 ($a_in $a_in 0) arc 3 7 ($ma_in $a_in 0) ); geometry { ball { type sphere; origin (0 0 0); radius $r_in; } ami { type sphere; origin (0 0 0); radius $r_ami; } } faces ( project ( 8 12 15 11) ami project (10 14 13 9) ami project ( 9 13 12 8) ami project (11 15 14 10) ami project ( 8 11 10 9) ami project (12 13 14 15) ami project (0 4 7 3) ball project (2 6 5 1) ball project (1 5 4 0) ball project (3 7 6 2) ball project (0 3 2 1) ball project (4 5 6 7) ball ); boundary ( in_to_out { type wall; faces ( ( 8 12 15 11) (10 14 13 9) ( 9 13 12 8) (11 15 14 10) ( 8 11 10 9) (12 13 14 15) ); } ball { type wall; faces ( (0 4 7 3) (2 6 5 1) (1 5 4 0) (3 7 6 2) (0 3 2 1) (4 5 6 7) ); } ); |
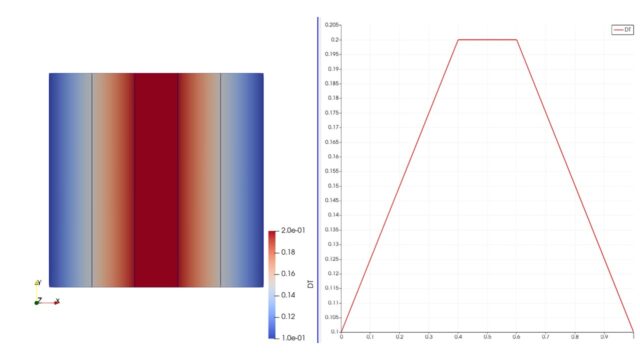
blockMeshを実行してできたメッシュがこちらです。
いちおうouterのメッシュの設定も載せおきます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 | scale 1; verbose yes; // basketball r = 0.125m //r_in 0.128; r_ami 0.148; a_out 1.5; ma_out #calc "-$a_out"; x_in -2.5; x_out 2.5; geometry { ami { type sphere; origin (0 0 0); radius $r_ami; } } n 24; t 48; n_in 6; n_out 6; v #calc "1.0/sqrt(3.0)"; a #calc "1.0/sqrt(2.0)"; v_ami #calc "$r_ami*$v"; mv_ami #calc "-$v_ami"; a_ami #calc "$r_ami*$a"; ma_ami #calc "-$a_ami"; vertices ( ($mv_ami $mv_ami $mv_ami) // 0 ( $v_ami $mv_ami $mv_ami) // 1 ( $v_ami $v_ami $mv_ami) // 2 ($mv_ami $v_ami $mv_ami) // 3 ($mv_ami $mv_ami $v_ami) // 4 ( $v_ami $mv_ami $v_ami) // 5 ( $v_ami $v_ami $v_ami) // 6 ($mv_ami $v_ami $v_ami) // 7 ($ma_out $ma_out $ma_out) // 8 ( $a_out $ma_out $ma_out) // 9 ( $a_out $a_out $ma_out) // 10 ($ma_out $a_out $ma_out) // 11 ($ma_out $ma_out $a_out) // 12 ( $a_out $ma_out $a_out) // 13 ( $a_out $a_out $a_out) // 14 ($ma_out $a_out $a_out) // 15 ($x_in $ma_out $ma_out) // 16 ($x_in $a_out $ma_out) // 17 ($x_in $a_out $a_out) // 18 ($x_in $ma_out $a_out) // 19 ($x_out $ma_out $ma_out) // 20 ($x_out $a_out $ma_out) // 21 ($x_out $a_out $a_out) // 22 ($x_out $ma_out $a_out) // 23 ); blocks ( hex ( 9 8 12 13 1 0 4 5) ($n $n $t) simpleGrading (1 1 0.01) hex (10 9 13 14 2 1 5 6) ($n $n $t) simpleGrading (1 1 0.01) hex (11 10 14 15 3 2 6 7) ($n $n $t) simpleGrading (1 1 0.01) hex ( 8 11 15 12 0 3 7 4) ($n $n $t) simpleGrading (1 1 0.01) hex ( 8 9 10 11 0 1 2 3) ($n $n $t) simpleGrading (1 1 0.01) hex (13 12 15 14 5 4 7 6) ($n $n $t) simpleGrading (1 1 0.01) hex (11 8 12 15 17 16 19 18) ($n $n $n_in) simpleGrading (1 1 1) hex (21 20 23 22 10 9 13 14) ($n $n $n_out) simpleGrading (1 1 1) ); edges ( arc 0 1 (0 $ma_ami $ma_ami) // 12 arc 2 3 (0 $a_ami $ma_ami) arc 6 7 (0 $a_ami $a_ami) arc 4 5 (0 $ma_ami $a_ami) arc 0 3 ($ma_ami 0 $ma_ami) // 16 arc 1 2 ($a_ami 0 $ma_ami) arc 5 6 ($a_ami 0 $a_ami) arc 4 7 ($ma_ami 0 $a_ami) arc 0 4 ($ma_ami $ma_ami 0) // 20 arc 1 5 ($a_ami $ma_ami 0) arc 2 6 ($a_ami $a_ami 0) arc 3 7 ($ma_ami $a_ami 0) ); faces ( project (0 4 7 3) ami project (2 6 5 1) ami project (1 5 4 0) ami project (3 7 6 2) ami project (0 3 2 1) ami project (4 5 6 7) ami ); boundary ( out_wall { type patch; faces ( ( 9 13 12 8) (11 15 14 10) ( 8 11 10 9) (8 16 19 12) (12 19 18 15) (15 18 17 11) (11 17 16 8) (9 20 23 13) (13 23 22 14) (14 22 21 10) (10 21 20 9) (15 12 13 14) ); } out_to_in { type wall; faces ( (0 4 7 3) (2 6 5 1) (1 5 4 0) (3 7 6 2) (0 3 2 1) (4 5 6 7) ); } inlet { type patch; faces ( (17 16 19 18) ); } outlet { type patch; faces ( (21 20 23 22) ); } ); |
innerとouterを重ねるとこんな感じです。
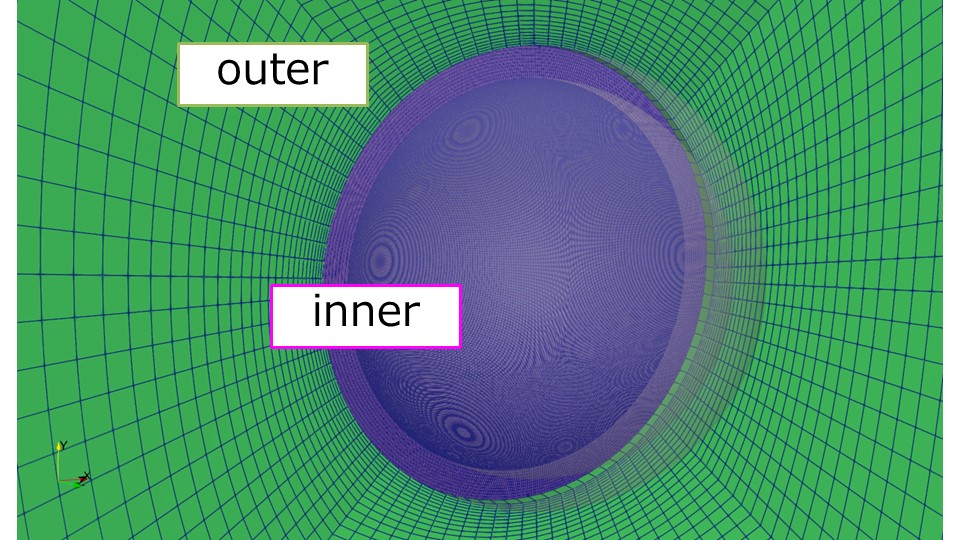
dynamicMeshでinnerをバスケットボール形状にフィットさせる
先ほどコピーしたdynamicMesh用のチュートリアルを参考に001_innerを編集していきます。
0/pointDisplacement
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | dimensions [0 1 0 0 0 0 0]; internalField uniform (0 0 0); boundaryField { ".*" { type fixedValue; value uniform (0 0 0); } ball { type surfaceDisplacement; value uniform (0 0 0); velocity (1e-3 1e-3 1e-3); geometry { basketball_m1.stl { type triSurfaceMesh; } }; projectMode pointNormal; projectDirection (1 1 1); wedgePlane -1; } } |
basketball_m1.stlは「constant/triSurface」に保存してあるバスケットボール形状のモデルです。速度「velocity (1e-3 1e-3 1e-3);」でバスケットボール形状にprojection（投影）する形でメッシュが変形していく設定です。
constant/dynamicMeshDict
1 2 3 4 5 6 7 | dynamicFvMesh dynamicMotionSolverFvMesh; motionSolverLibs (fvMotionSolvers); motionSolver displacementSBRStress; diffusivity quadratic inverseDistance (ball); |
inverseDistanceは境界面「ball」と一緒に動く設定です。
距離に応じで自然とメッシュがついてくるようにまわりのメッシュが変形してくれます。
「constant/controlDict」も必要に応じて変更します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | application moveDynamicMesh; startFrom startTime; startTime 0; stopAt endTime; endTime 30; deltaT 1; writeControl timeStep; writeInterval 5; purgeWrite 0; writeFormat binary; writePrecision 6; writeCompression off; timeFormat general; timePrecision 6; runTimeModifiable yes; |
設定が終わったら以下のコマンドでmoveDynamicMeshを実行します。
1 | moveDynamicMesh |
メッシュ数が多いので計算時間は少しかかります。
変形速度が速すぎたり、計算時間が長いと変形しすぎてしまうので、速度は微調整して適当にいい感じでメッシュ変形できたところで計算をストップして使えば良いかなと思います。
001_innerと002_outerのメッシュを結合すればバスケットボール形状の周りの流体の解析領域のメッシュが完成します。
1 2 | cp -r 001_inner 003_merge mergeMeshes 003_merge 002_outer -overwrite |
おまけ
バスケットボール形状でのシミュレーションも行って抗力係数を出してみました。
無回転での解析ですが結果は球体の抗力係数とたいして変わらないという結果でした。
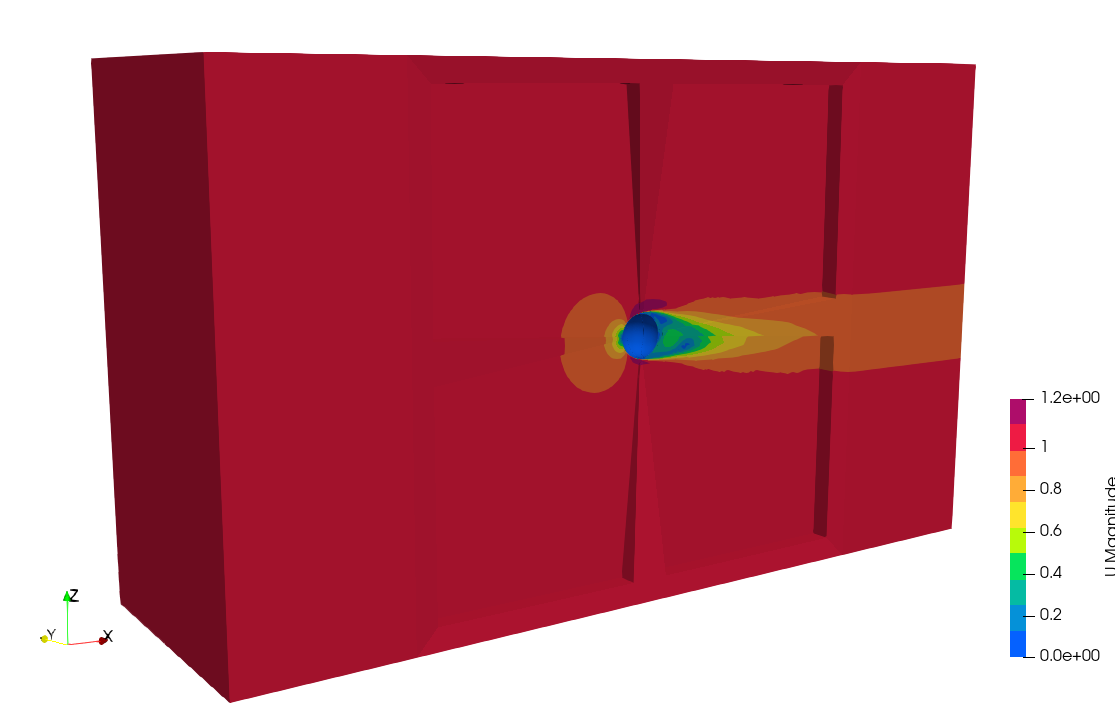
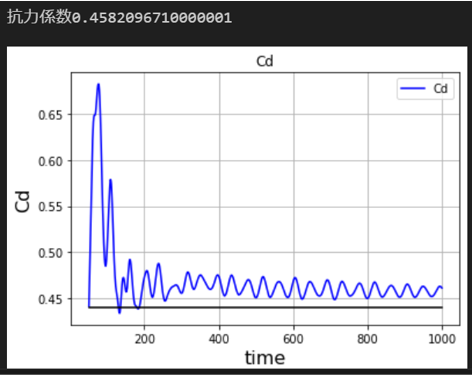
適当に作ったので流体領域はもう少しこだわった方が良さそうです。
具体的には、
- 流入側の領域は無駄に広いのでもう少し狭くする
- 流出側ももう少し解析領域を広くする
メッシュ数が多く（1000万程度）今回はテスト計算しかしていないので、暇があればトライしたいと思います_(._.)_
また、今回は渦が放出する非定常の現象を定常解析(simpleFoam）で行いましたので、厳密な実現象の再現にはなっていないかもしれません。
おすすめ参考図書
☟こちらは、OpenFOAMの日本語書籍として重宝しているわかりやすい参考書だと思います。
☟こちらもOpenFOMの古いバージョンでの和訳になります。さすがにこちらはバージョンに対する日本語でのケアはしていないので、OpenFOAMに慣れている方は購入しても良いかと思います。僕は「日本語でまとまっている内容」なので少し重宝しています。
☟以下に、もっと初心者向けの同人誌を紹介しておきます。
初心者は「ってか、まずどうやってOpenFOAMをインストールするの？」というところからつまずきがちです。
そんな時は、以下の書籍をおすすめします。
改訂新版 OpenFOAMの歩き方 (技術の泉シリーズ（NextPublishing）)
インストール方法とチュートリアルで流体解析を体験・・・ちょっと高度な解析まで解説があります。著者曰くOpenFOAMのバージョンの追跡を行いながら、書籍をアップデートするようなので安心ですね。
OpenFOAMコードの辞書的な扱いとしては以下の参考書が大変役に立ちます。
本記事ではESI版のOpenFOAMを使っているため本書のFoundation版で対応していない部分がありますが、その辺を考慮しても持っていて損はないでしょう。
今回の記事はこちらの著者の方からモデル提供をいただきモデル作成の解説を行いました。
OpenFOAMでメッシュ作成
Follow @t_kun_kamakiri