ラグランジュ方程式からハミルトンの正準方程式の導出

今日はですね～普通に「ハミルトンの正準方程式」を導出したいと思います。

普通って何が普通？(笑）って感じですけど、「ランダウ＝リフシッツの”力学”」に書いてある通りに、素直なやり方で導出します。

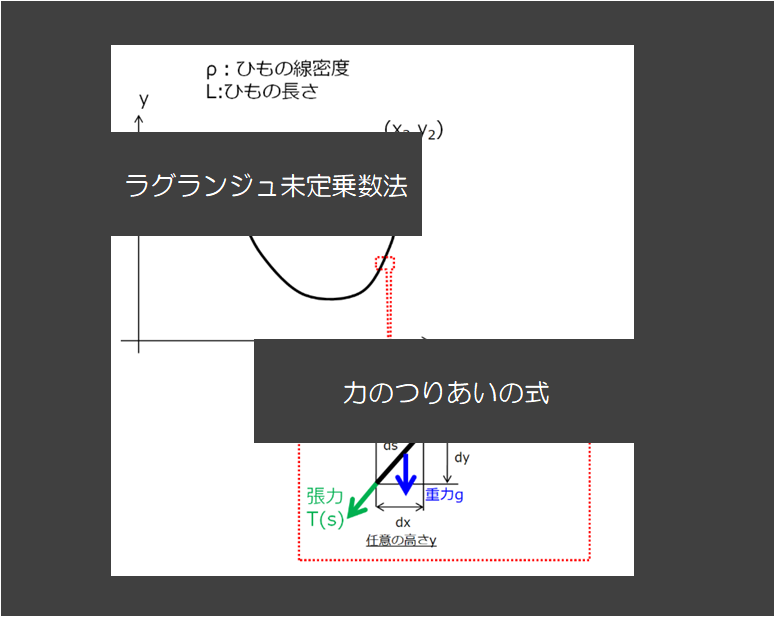
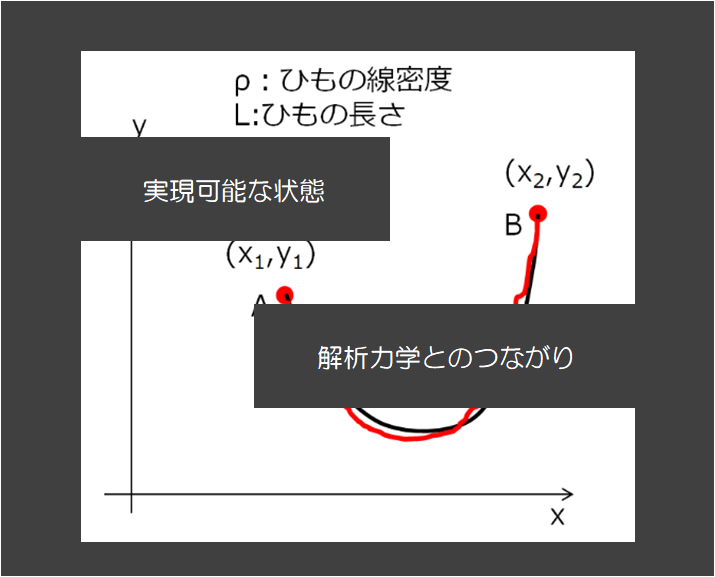
前回までは、↓下記のようにルジャンドル変換とかを使ってハミルトンの正準方程式を導出したのですけど、それに比べたらこの記事の内容の方が易しいと思います(笑)

前回の記事はこちら

さて、やっていきましょう(^^)/

ハミルトンの正準方程式の意図
ハミルトンの正準方程式の導出
次回

ハミルトンの正準方程式の意図

ラグランジアン\(L(\{q_{i}\},\{\dot{q}_{i}\})\)が求まりさえすれば、

それをラグランジュ方程式\(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial {q}_{i}}\)に代入すれば、

力学的状態を記述するための運動方程式が導かれるのに、

「どうしてわざわざはハミルトンの正準方程式などどいう等価な方程式を導く必要があるのか」というように思います。

ラグランジアン\(L(\{q_{i},\{\dot{q}_{i}\})\)は、陽に時間に依存しないとすれば、それぞれ独立の変数である一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)によって力学的な状態が記述されます。

それを、それぞれ独立の変数である一般座標\(q_{i}\)と一般運動量\(p_{i}\)にして力学的な状態を記述するようにしても良いのです。

それが、ハミルトンの正準方程式です。

ハミルトンの正準方程式
ハミルトニアン\(H(\{q_{i}\},\{p_{i}\})\)に対して
\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (1)\end{align*}
\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (2)\end{align*}

このように見てもとても対称性がよいですね。

あともうひとつ・・・

一般座標\(q_{i}\)と一般運動量\(p_{i}\)は互いに独立であるとしていました。

それを例えば、新しい変数\(Q_{i}=Q_{i}(\{q_{i}\},\{p_{i}\},t)\)と\(P_{i}=P_{i}(\{q_{i}\},\{p_{i}\},t)\)を作ってハミルトンの正準方程式を拡張することだってできます。

これは正準変換というものでして、追々記事上げていきます。
※ここでは深くは触れません。

なので、(1)(2)式のような形であるハミルトンの正準方程式にする方が扱いやすいのです。

ハミルトンの正準方程式の導出

さて前置きはこれくらいにして、導出しましょう(^^)/

今まで得た知見は下記のとおりです。

ラグランジアン：
\begin{align*}L(\{q_{i}\},\{\dot{q}_{i}\})\cdot\cdot\cdot (3)\end{align*}
ラグランジュ方程式：
\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial {q}_{i}}\cdot\cdot\cdot (4)\end{align*}
運動量：
\begin{align*}p_{i}=\frac{\partial L}{\partial \dot{q}_{i}}\cdot\cdot\cdot (5)\end{align*}

前回の記事はこちら

まず、ラグランジアン\(L(\{q_{i}\},\{\dot{q}_{i}\})\)の全微分を考えます。

\begin{align*}dL=\sum_{i}\frac{\partial L}{\partial q_{i}}d q_{i}+\sum_{i}\frac{\partial L}{\partial \dot{q}_{i}}d \dot{q}_{i}\cdot\cdot\cdot (6)\end{align*}

右辺第一項に(4)式を、右辺第二項に(5)式を代入します。

\begin{align*}dL=\sum_{i}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}d q_{i}+\sum_{i}p_{i}d \dot{q}_{i}\end{align*}

さらに右辺第一項に(5)式を使います。

\begin{align*}dL=\sum_{i}\dot{p}_{i}d q_{i}+\sum_{i}p_{i}d \dot{q}_{i}\cdot\cdot\cdot (7)\end{align*}

右辺第二項について、

\begin{align*}d(p_{i}\dot{q}_{i})=p_{i}d\dot{q}_{i}+\dot{q}_{i}dp_{i}\end{align*}

⇔

\begin{align*}p_{i}d\dot{q}_{i}=d(p_{i}\dot{q}_{i})-\dot{q}_{i}dp_{i}\end{align*}

として、これを(7)式に代入しましょう。

\begin{align*}dL=\sum_{i}\dot{p}_{i}d q_{i}+\sum_{i}d(p_{i}\dot{q}_{i})-\sum_{i}\dot{q}_{i}dp_{i}\end{align*}

これを、↓こうしましょう。

\begin{align*}d\big(\sum_{i}p_{i}\dot{q}_{i}-L\big)=\sum_{i}(-\dot{p}_{i})d q_{i}+\sum_{i}\dot{q}_{i}dp_{i}+\cdot\cdot\cdot (8)\end{align*}

そうすると、左辺はエネルギー量になっています。
↓こちらを参照ください。

前回の記事はこちら

エネルギー保存則：時間対称（ネーターの定理）：ランダウ=リフシッツの”力学”

エネルギーが座標と運動量で表されているとき、それをハミルトニアン\(H\)といます。

\begin{align*}H=\sum_{i}p_{i}\dot{q}_{i}-L\end{align*}

とおくと(8)式は、

\begin{align*}dH=\sum_{i}(-\dot{p}_{i})d q_{i}+\sum_{i}\dot{q}_{i}dp_{i}+\cdot\cdot\cdot (9)\end{align*}

(9)式は\(\{q_{i}\}\)と\(\{p_{i}\}\)を変数とするハミルトニアン\(H\)に対する全微分の形になっています。
↓\(H\)の全微分はこんな感じです。

\begin{align*}dH=\sum_{i}\frac{\partial H}{\partial q_{i}}d q_{i}+\sum_{i}\frac{\partial H}{\partial p_{i}}d p_{i}\cdot\cdot\cdot (10)\end{align*}

ここで、(9)式と(10)式を比較すると・・・・

\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (1)\end{align*}

\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (2)\end{align*}

とこうなるわけですね～(^^)/

まとめ：
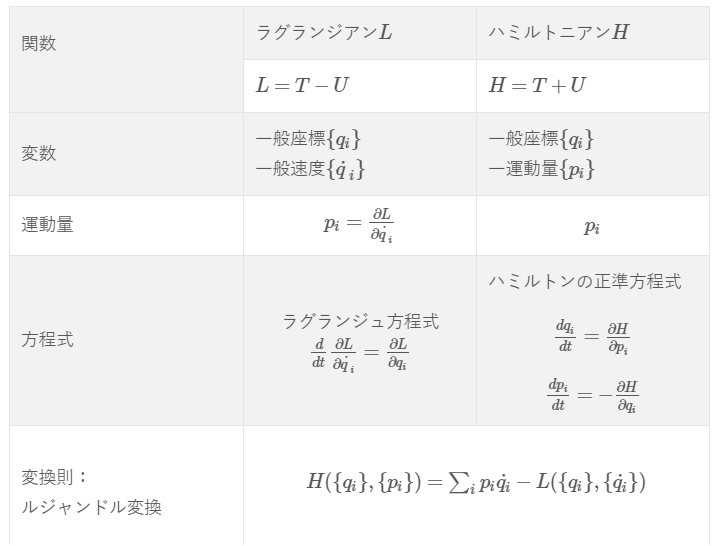
ラグランジアン\(L\)とハミルトン\(H\)の対応関係

関数	ラグランジアン\(L\)	ハミルトニアン\(H\)
関数	\(L=T-U\)	\(H=T+U\)
変数	一般座標\(\{q_{i}\}\) 一般速度\(\{\dot{q}_{i}\}\)	一般座標\(\{q_{i}\}\) 一運動量\(\{p_{i}\}\)
運動量	\(p_{i}=\frac{\partial L}{\partial \dot{q}_{i}}\)	\(p_{i}\)
方程式	ラグランジュ方程式 \(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial {q}_{i}}\)	ハミルトンの正準方程式 \(\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\) \(\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\)
変換則：ルジャンドル変換	\(H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\)