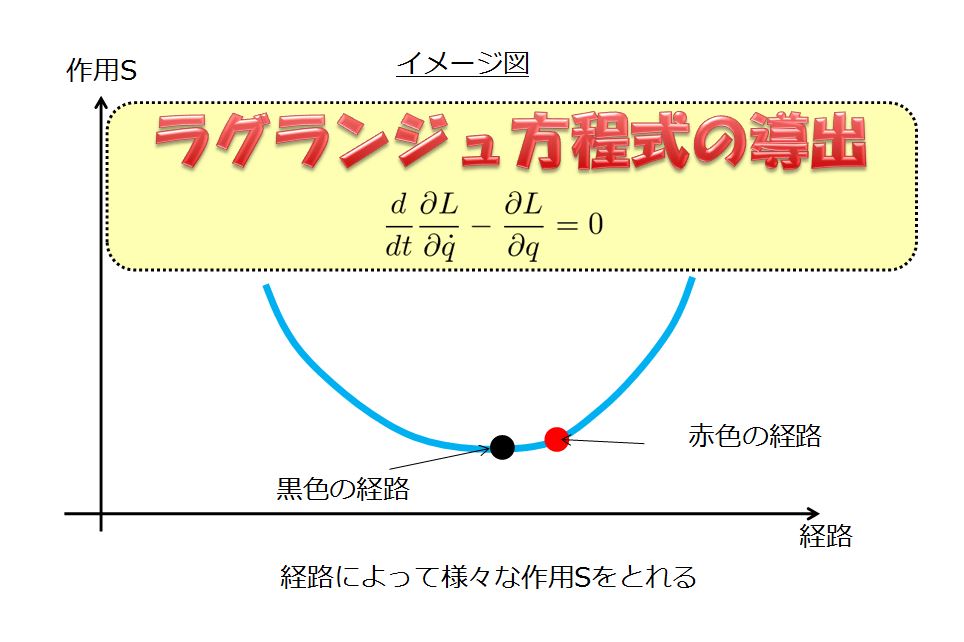
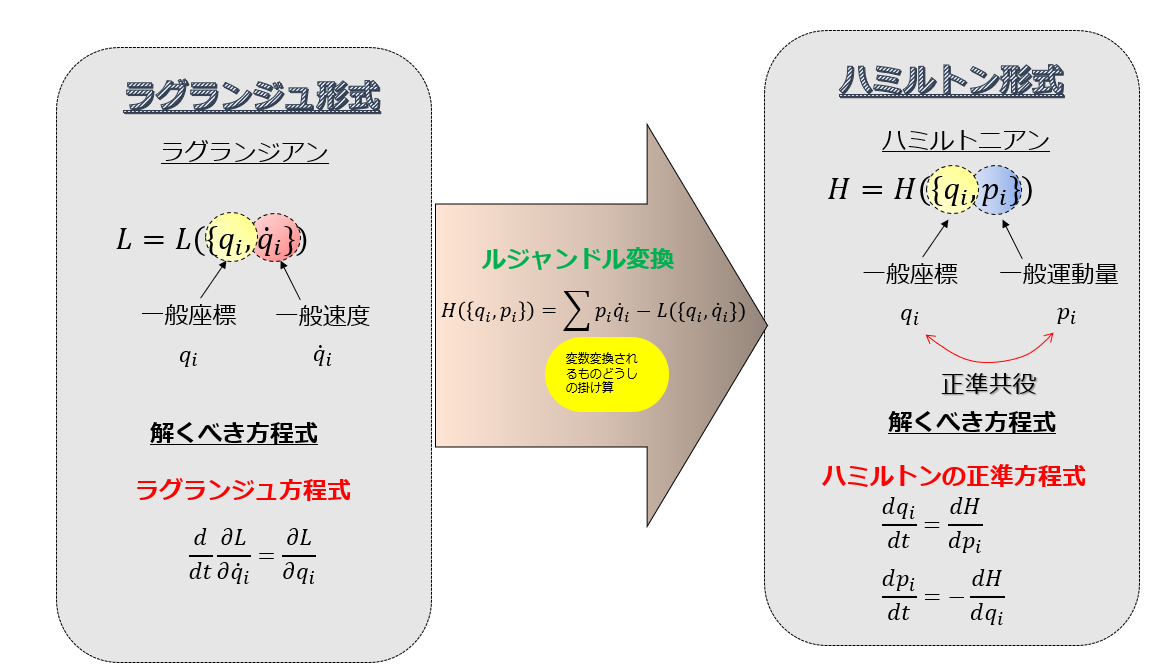
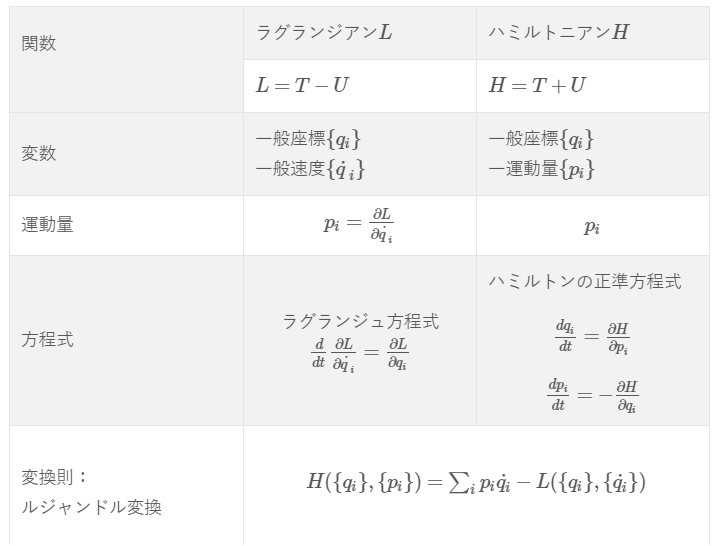
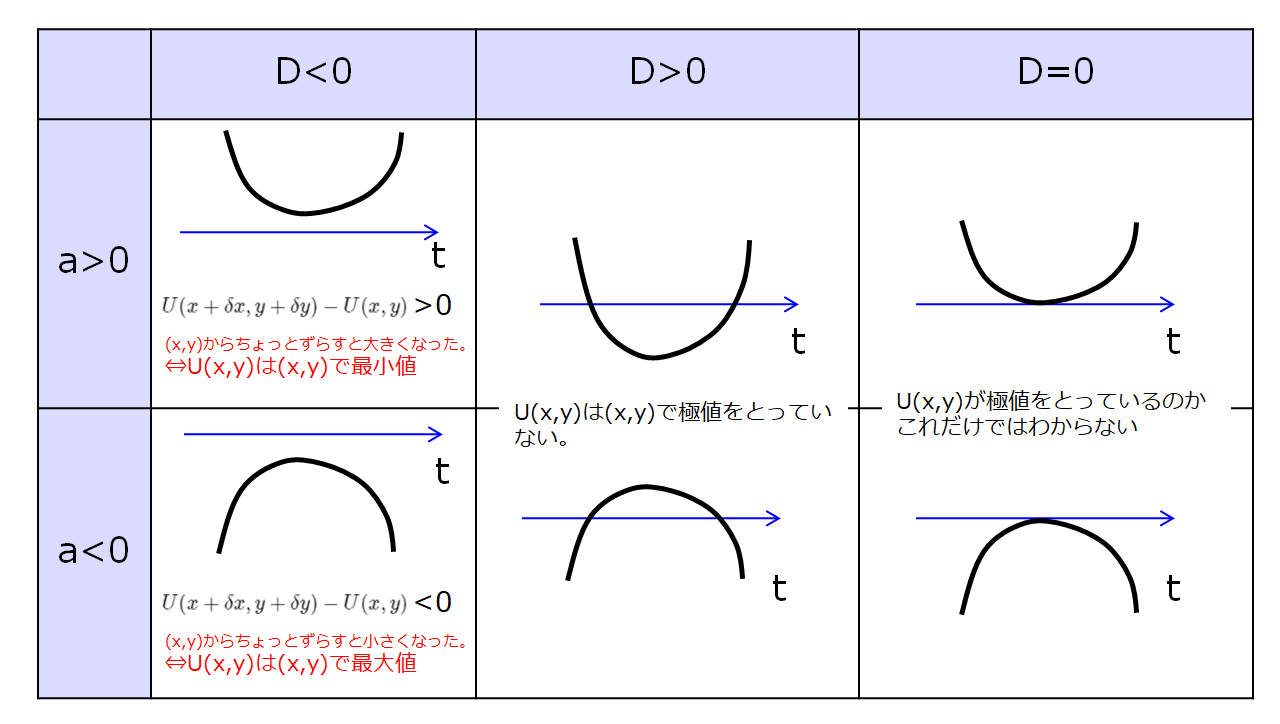
前回は、一般速度\(\dot{q}_{i}\)を部分的に変換するラウシアンというのを紹介しました。
紹介したと言っても表にまとめてみただけです(笑)
そして本日はその続きで、ラウシアンを導入するまでの手続きをゴリゴリ式を書きながらやっていきたいと思います。
部分的に変換してラウシアンの導入
独立な変数が、
一般座標:\(q_{1},q_{2},\cdot\cdot\cdot,q_{i},\cdot\cdot\cdot,q_{m},\xi_{1},\xi_{2},\cdot\cdot\cdot,\xi_{j},\cdot\cdot\cdot,\xi_{n}\)
一般速度:\(\dot{q}_{1},\dot{q}_{2},\cdot\cdot\cdot\dot{q}_{i},\cdot\cdot\cdot,\dot{q}_{m},\dot{\xi}_{1},\dot{\xi}_{2},\cdot\cdot\cdot,\dot{\xi}_{j},\cdot\cdot\cdot,\dot{\xi}_{n}\)
であるとします。
見にくいので↓下記のように書きます。
一般座標:\(\{q_{i}\},\{\xi_{j}\}\) (\(i=1~m\))
一般速度:\(\{\dot{q}_{i}\},\{\dot{\xi}_{j}\}\) (\(j=1~n\))
そうするとラグランジアンは、
\begin{align*}L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\cdot\cdot\cdot (1)\end{align*}
と書けます。
全部で\(m+n=f\)個の自由度があるものとします。
一般座標\(\{q_{i}\}\)については、一般運動量\(\{p_{i}\}\)との間には
\begin{align*}p_{i}=\frac{\partial L}{\partial \dot{q_{i}}}\cdot\cdot\cdot (2)\end{align*}
が成り立ちます。
前回の記事はこちら
\(\dot{\xi}_{j}\)については、一般運動量に変換しないつもりなので、②のような関係式は導入しません。
あとは、両者ラグランジュ方程式を満たしますので、↓こちらも用意しておきましょう。
\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial q_{i}}\cdot\cdot\cdot (3)\end{align*}
\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{\xi}_{j}}=\frac{\partial L}{\partial \xi_{j}}\cdot\cdot\cdot (4)\end{align*}
ラグランジアンの全微分
ラグランジアン
\begin{align*}L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\cdot\cdot\cdot (5)\end{align*}
に対して、全微分を考えます。
\begin{align*}dL=\sum_{i}\frac{\partial L}{\partial q_{i}}dq_{i}+\sum_{j}\frac{\partial L}{\partial \xi_{i}}d\xi_{i}\end{align*}
\begin{align*}+\sum_{i}\frac{\partial L}{\partial \dot{q}_{i}}d\dot{q}_{i}+\sum_{j}\frac{\partial L}{\partial \dot{\xi}_{j}}d\dot{\xi}_{j}\cdot\cdot\cdot (5)\end{align*}
※今、ラグランジアンは時間\(t\)に陽に依存しないとしています。
さて、式変形を続けます。
(5)式第一項について
まずは(3)式を使い、その後(2)式を使います。
\begin{align*}\frac{\partial L}{\partial q_{i}}dq_{i}=\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}dq_{i}=\frac{d}{dt}p_{i}dq_{i}=\dot{p}_{i}dq_{i}\end{align*}
(5)式第三項について
(2)式を使います。
\begin{align*}\frac{\partial L}{\partial \dot{q}_{i}}d\dot{q}_{i}=p_{i}d\dot{q}_{i}\end{align*}
これらを(5)式に代入します。
\begin{align*}dL=\sum_{i}\dot{p}_{i}dq_{i}+\sum_{j}\frac{\partial L}{\partial \xi_{j}}d\xi_{j}\end{align*}
\begin{align*}+\sum_{i}p_{i}d\dot{q}_{i}+\sum_{j}\frac{\partial L}{\partial \dot{\xi}_{j}}d\dot{\xi}_{j}\cdot\cdot\cdot (6)\end{align*}
次は、(6)式の第三項\(p_{i}d\dot{q}_{i}\)に着目します。
\begin{align*}d(p_{i}\dot{q}_{i})=p_{i}d\dot{q}_{i}+\dot{q}_{i}dp_{i}\end{align*}
ですので、これの第一を使います。
そうすると(6)式は、
\begin{align*}dL=\sum_{i}\dot{p}_{i}dq_{i}+\sum_{j}\frac{\partial L}{\partial \xi_{j}}d\xi_{j}\end{align*}
\begin{align*}+\sum_{i}d(p_{i}\dot{q}_{i})-\sum_{i}\dot{q}_{i}dp_{i}+\sum_{j}\frac{\partial L}{\partial \dot{\xi}_{j}}d\dot{\xi}_{j}\end{align*}
⇔全部の符号を反転、第三項を移行
\begin{align*}d(\sum_{i}p_{i}\dot{q}_{i}-L)\end{align*}
\begin{align*}=\sum_{i}(-\dot{p}_{i})dq_{i}+\sum_{j}\big(-\frac{\partial L}{\partial \xi_{j}}\big)d\xi_{j}+\sum_{i}\dot{q}_{i}dp_{i}+\sum_{j}\big(-\frac{\partial L}{\partial \dot{\xi}_{j}}\big)d\dot{\xi}_{j}\cdot\cdot\cdot (7)\end{align*}
↑こんな感じになりました。
ラウシアン(ラウス関数)の導入
さて、いよいよラウシアン(ラウス関数)を導入しましょう(^^)/
\begin{align*}d(\sum_{i}p_{i}\dot{q}_{i}-L)\end{align*}
\begin{align*}=\sum_{i}(-\dot{p}_{i})dq_{i}+\sum_{j}\big(-\frac{\partial L}{\partial \xi_{j}}\big)d\xi_{j}+\sum_{i}\dot{q}_{i}dp_{i}+\sum_{j}\big(-\frac{\partial L}{\partial \dot{\xi}_{j}}\big)d\dot{\xi}_{j}\cdot\cdot\cdot (7)\end{align*}
(7)式の左辺の全微分の形ですが、ラウシアン(ラウス関数)を導入します。
\begin{align*}R=\sum_{i}p_{i}\dot{q}_{i}-L\cdot\cdot\cdot (8)\end{align*}
変数がわかるように書くと、
\begin{align*}R(\{q_{i}\},\{\xi_{i}\},\{p_{i}\}\{\dot{\xi}_{i}\})=\sum_{i}p_{i}\dot{q}_{i}-L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\end{align*}
ごちゃごちゃしていますが、よーく見ると、
\(\{\dot{q}_{i}\}\)が\(\{p_{i}\}\)に変わっていますよ。
そしたら(7)式が、
\begin{align*}dR=\sum_{i}(-\dot{p}_{i})dq_{i}+\sum_{j}\big(-\frac{\partial L}{\partial \xi_{j}}\big)d\xi_{j}\end{align*}
\begin{align*}+\sum_{i}\dot{q}_{i}dp_{i}+\sum_{j}\big(-\frac{\partial L}{\partial \dot{\xi}_{j}}\big)d\dot{\xi}_{j}\cdot\cdot\cdot (9)\end{align*}
と書けますね。
ラウシアン(ラウス関数)の全微分
ラウシアン(ラウス関数)の全微分を考えます。
(5)式と同じ感じでするだけです。
\begin{align*}dR=\sum_{i}\frac{\partial R}{\partial q_{i}}dq_{i}+\sum_{j}\frac{\partial R}{\partial \xi_{i}}d\xi_{i}\end{align*}
\begin{align*}+\sum_{i}\frac{\partial R}{\partial p_{i}}dp_{i}+\sum_{j}\frac{\partial R}{\partial \dot{\xi}_{j}}d\dot{\xi}_{j}\cdot\cdot\cdot (10)\end{align*}
そして、これと(9)式
\begin{align*}dR=\sum_{i}(-\dot{p}_{i})dq_{i}+\sum_{j}\big(-\frac{\partial L}{\partial \xi_{j}}\big)d\xi_{j}\end{align*}
\begin{align*}+\sum_{i}\dot{q}_{i}dp_{i}+\sum_{j}\big(-\frac{\partial L}{\partial \dot{\xi}_{j}}\big)d\dot{\xi}_{j}\cdot\cdot\cdot (9)\end{align*}
とを比較します。
すると、
\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial R}{\partial q_{i}}\cdot\cdot\cdot (11)\end{align*}
\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial R}{\partial p_{i}}\cdot\cdot\cdot (12)\end{align*}
\begin{align*}\frac{\partial L}{\partial \xi_{j}}=-\frac{\partial R}{\partial \xi_{j}}\cdot\cdot\cdot (13)\end{align*}
\begin{align*}\frac{\partial L}{\partial \dot{\xi}_{j}}=-\frac{\partial R}{\partial \dot{\xi}_{j}}\cdot\cdot\cdot (14)\end{align*}
(11)(12)は、見るからにハミルトンの正準方程式と同じ形ですね!(^^)!
(13)(14)をもう少し式変形します。
と、言ってももとのラグランジュ方程式に代入するだけです(笑)。
\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \dot{\xi}_{j}}=\frac{\partial L}{\partial \xi_{j}}\cdot\cdot\cdot (14)\end{align*}
これに(13)(14)式を代入すると
\begin{align*}\frac{d}{dt}\frac{\partial R}{\partial \dot{\xi}_{j}}=\frac{\partial R}{\partial \xi_{j}}\cdot\cdot\cdot (15)\end{align*}
\(L\)が\(R\)に変わっただけですね。
ということで、下記のように式がすっきりしました!(^^)!
\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial R}{\partial q_{i}}\cdot\cdot\cdot (11)\end{align*}
\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial R}{\partial p_{i}}\cdot\cdot\cdot (12)\end{align*}
\begin{align*}\frac{d}{dt}\frac{\partial R}{\partial \dot{\xi}_{j}}=\frac{\partial R}{\partial \xi_{j}}\cdot\cdot\cdot (15)\end{align*}
系のエネルギー
エネルギーについては↓こちらの記事をご参考ください。
前回の記事はこちら
\(q_{i}\)や\(\dot{q}_{i}\)だけだと、
\begin{align*}E=\sum_{i}\frac{\partial L}{\partial \dot{q}_{i}}\dot{q}_{i}-L\end{align*}
こうなのですが、
今は、\(q_{i}\)、\(\dot{q}_{i}\)、\(\xi_{i}\)、\(\dot{\xi}_{i}\)と変数を書いているので、
\begin{align*}E=\sum_{i}\frac{\partial L}{\partial \dot{q}_{i}}\dot{q}_{i}+\sum_{j}\frac{\partial L}{\partial \dot{\xi}_{j}}\dot{q}_{j}-L\cdot\cdot\cdot (16)\end{align*}
と書きます。
第一項については、(2)を使いますので、
\begin{align*}E=\sum_{i}p_{i}\dot{q}_{i}+\sum_{j}\frac{\partial L}{\partial \dot{\xi}_{j}}\dot{q}_{j}-L\end{align*}
さらに、(8)(14)式を使うと、
\begin{align*}E=R-\sum_{j}\frac{\partial L}{\partial \dot{\xi}_{j}}\dot{q}_{j}\cdot\cdot\cdot (17)\end{align*}
まとめ
何をしたくて、何をしたかをまとめます。
何をしたいか
一般座標:\(\{q_{i}\},\{\xi_{j}\}\) (\(i=1~m\))
一般速度:\(\{\dot{q}_{i}\},\{\dot{\xi}_{j}\}\) (\(j=1~n\))
として、ラグランジアンは
\begin{align*}L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\cdot\cdot\cdot (1)\end{align*}
ですが、一般速度\(\{\dot{q}_{i}\}\)だけ一般運動量\(\{p_{i}\}\)に変えたい。
一般速度\(\{\dot{\xi}_{j}\}\)については一般速度\(\{\dot{\xi}_{j}\}\)のままにしておく。
何をしたか
ラウシアン(ラウス関数)
\begin{align*}R=\sum_{i}p_{i}\dot{q}_{i}-L\cdot\cdot\cdot (8)\end{align*}
※変数を書くと、\(R(\{q_{i}\},\{\xi_{i}\},\{p_{i}\}\{\dot{\xi}_{i}\})=\sum_{i}p_{i}\dot{q}_{i}-L(\{q_{i}\},\{\xi_{i}\},\{\dot{q}_{i}\}\{\dot{\xi}_{i}\})\)
を導入して、\(\{\dot{q}_{i}\}\)が\(\{p_{i}\}\)に変換。
すると、
\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial R}{\partial q_{i}}\cdot\cdot\cdot (11)\end{align*}
\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial R}{\partial p_{i}}\cdot\cdot\cdot (12)\end{align*}
\begin{align*}\frac{d}{dt}\frac{\partial R}{\partial \dot{\xi}_{j}}=\frac{\partial R}{\partial \xi_{j}}\cdot\cdot\cdot (15)\end{align*}
\(\{q_{i}\}\)や\(\{p_{i}\}\)についてはハミルトンの正準方程式を使い、
\(\{\xi_{i}\}\)や\(\{\dot{\xi}_{i}\}\)についてはそのままラグランジュ方程式を使うということになります。
系のエネルギーは、
\begin{align*}E=R-\sum_{j}\frac{\partial L}{\partial \dot{\xi}_{j}}\dot{q}_{j}\cdot\cdot\cdot (17)\end{align*}
と書けます。
こんな部分的に変数を変換して、何が嬉しいのか?
こちらについては、例題を考えて更新したいと思いますので、少々お待ち下さいm(- -)m