下記の記事で正準変換についてまとめ、その後母関数の変換についての記事を書きました。
本記事は、上記2つのまとめをしたいと思います(^^)/
やっと正準変換の嬉しさがひとつわかった気がします(笑)
正準変換の嬉しさとは
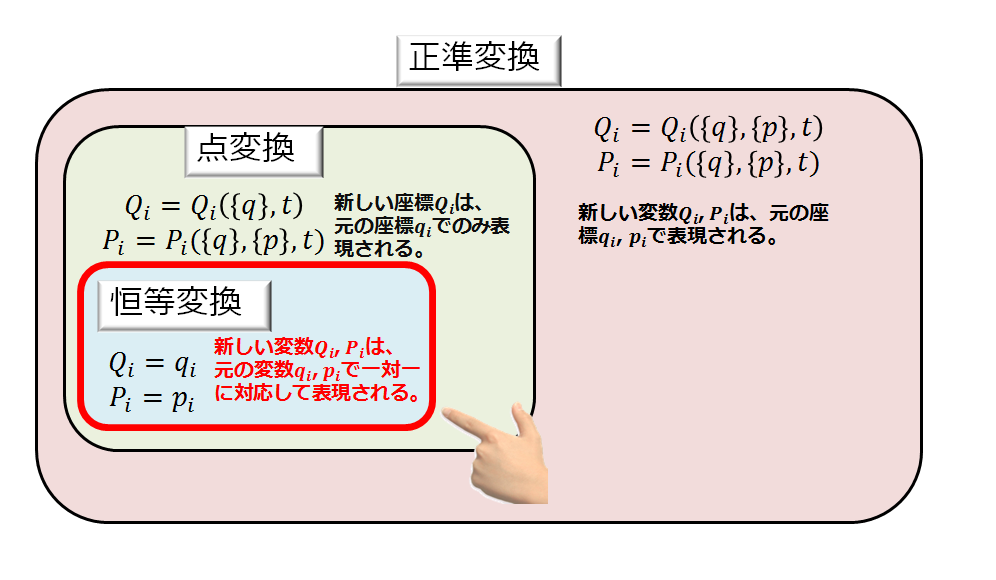
正準変換とは:復習
↓この記事でも詳しく書いていますが、ここでは概要を書いていきます。
ハミルトン形式では一般座標\(\{q_{i}\}\)と一般運動量\(\{p_{i}\}\)を指定することで<<力学的な状態>>は定まります。
位相空間内ではそれらを変数とした状態点として定まります。
その状態点の初期状態(\(\{q_{i}(0)\},\{p_{i}(0)\}\))を決めれば、あとは系の運動はハミルトンの正準方程式に従って時間発展して、時刻歴変化として系の状態が決定されます。
なので僕たちがすることはハミルトニアンの正準方程式を立て、それを手計算でも数値計算でも良いので解ければ、問題は解けたことになります。
ただ、そんな都合よくハミルトンの正準方程式を立てたからと言って問題が解けたとはとても言い難いのです。
なぜなら、方程式は立てることができても解析的に(手計算で)解けるほど方程式がシンプルでかつ閉じているとは限らないからです。
では数値計算で解けば良いではないかと言っても、もとの式が単純だと離散化するのもちょっと面倒なのです。
いかに方程式をシンプルな形にするかの方が大事なのです。
そこで、今まで議論してきた解析力学の枠組みさえ外れずにもっと良い変数の選び方ができるはずです。
そして次のことを考えるわけです。
解析力学の枠組みでこのように座標の変換に対して基礎方程式(ラグランジュ方程式、ハミルトンの正準方程式)が変わらないとするだけでなくて、一般座標と一般運動量も含めて(すなわち、運動量も座標と同等の独立変数として扱う)、ハミルトンの正準方程式の形を不変に保つように変数変換しよう。
式で書くと、
↑そういう変換ができるはずです。
これを正準変換と言います。
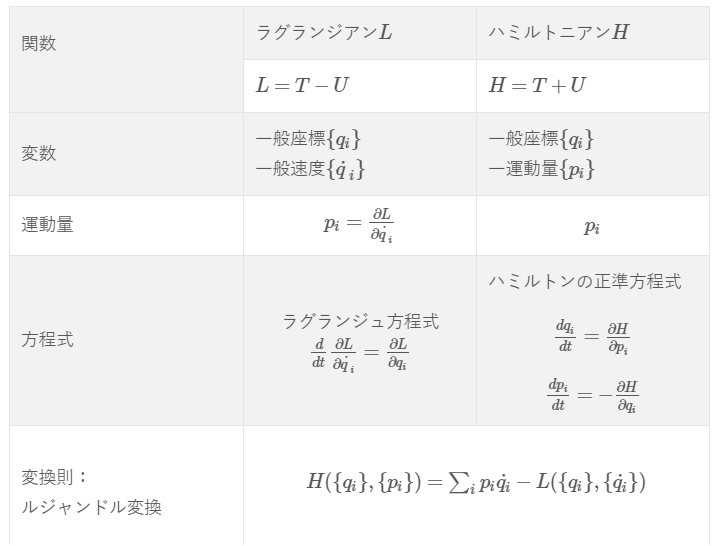
ハミルトンの正準方程式の形を不変に保つようにするので、変換後も
ハミルトンの正準方程式
が成り立るようにさえしていれば、ハミルトン形式から外れていないのでOKではないかと考えているのです。
ただデタラメに変換していつでも都合の良いように③④式が成り立つわけがないので、そうなるための条件が存在します。
です。
これさえ満たしていれば、③④式を使っても文句ないでしょうというのが出てきます。
ここで、\(W_{1}\)のことを母関数と言い正準変換はこの関数によって特徴づけられます。
母関数\(W_{1}\)の変数はここでは\(\{q_{i}\}\)と\(\{Q_{i}\}\)です。
しかし、あとで触れますが母関数の変数の選び方は\(\{q_{i}\}\)と\(\{Q_{i}\}\)だけではありません。
元の変数\(\{q_{i}\}\)と\(\{p_{i}\}\)から一組選び、新しい変数\(\{Q_{i}\}\)と\(\{P_{i}\}\)から一組選ぶ方法の合計4パターンの変数の選び方があるのです。
※本記事の後半でまとめを記載しています。
正準変換の嬉しさ
正準変換をする嬉しさは上でも少し書きましたが、
「もっと良い変数の選び方ができる」はずと思って変数を変換したのです。
単なる数学的なお遊びではなかったのです(笑)
正準変換を上手に(どうやってするかは具体的にはわかりませんが(笑))変換することを考えます。
上手にとは、
もともとのハミルトニアン
に対して正準変換を施して、\(k\)番目の座標\(Q_{k}\)に依存しないハミルトニアン\({H}’\)にできたとしましょう。
このような座標のことを循環座標と言います。
※正準変換しているので座標と言うのか・・・(?)
つまり、
これができるととても嬉しい!!
なぜなら(4)式より、
⇔
一般運動量が定数になった!!(‘▽’)
正準変換を行って、ハミルトニアン\({H}’\)が一般座標を含まないようにすることができれば問題はとても解きやすくなります。
いや、解けたと言っていいでしょう。
なぜなら、その場合はハミルトニアンは
とこうなっているのです。
そして(3)式を使って、
※右辺は\(P_{i}\)でまず微分して、\(P_{i}=\alpha_{i}\)を代入するという意味です。
たまに、\({H}’\)に\(\alpha_{i}\)を代入してから微分して0ですね・・・ってなっている人もいますが、気を付けましょう(笑)
これを積分すれば、
※\(Q_{i}(0)\)は初期状態
となります。
つまり、初期状態の\(Q_{i}(0)\)を与えればその時間発展は、
\begin{align*}Q_{i}=\int \frac{\partial {H}’}{\partial P_{i}}|_{ P_{i}=\alpha_{i}}+Q_{i}(0)\cdot\cdot\cdot (12)\end{align*}
\begin{align*}P_{k}=\alpha_{k}=const\cdot\cdot\cdot (9)\end{align*}
として求まるため、原理的には問題は解けたことになります。
もとの\(\{q_{i}\}\)や\(\{p_{i}\}\)の戻したいときは、①②からもできるでしょうし、母関数を通して⑤⑥式からでもできるしょう。
こうして正準変換の嬉しさを見出すことができたのです。
母関数のまとめ
ここでの母関数\(W_{1}\)の変数は\(\{q_{i}\}\)と\(\{Q_{i}\}\)ですが、母関数の変数の選び方は\(\{q_{i}\}\)と\(\{Q_{i}\}\)だけではありません。
というのを導出も含めて下記の記事に書きました。
ざっくりと言ってしまえば、
元の変数\(\{q_{i}\}\)と\(\{p_{i}\}\)から一組選び、新しい変数\(\{Q_{i}\}\)と\(\{P_{i}\}\)から一組選ぶ方法の合計4パターンの変数の選び方があるのです。
母関数 |
母関数の変換 |
元の変数 |
新しい変数 |
ハミルトニアン | ||
| \(q_{i}\) | \(p_{i}\) | \(Q_{i}\) | \(P_{i}\) | \({H}’\) | ||
|
\(W_{1}\) 変数 \(\{q_{i}\}\), \(\{Q_{i}\}\) |
\(W_{1}\) | \(\frac{\partial W_{1}}{\partial q_{i}}\) | \(-\frac{\partial W_{1}}{\partial Q_{i}}\) | \(H+\frac{\partial W_{1}}{\partial t}\) | ||
|
\(W_{2}\) 変数 \(\{q_{i}\}\), \(\{P_{i}\}\) |
\(W_{2}=W_{1}+\sum_{i}P_{i}Q_{i}\) \(W_{2}=W_{1}+\sum_{i}P_{i}Q_{i}\) |
\(\frac{\partial W_{2}}{\partial q_{i}}\) | \(\frac{\partial W_{2}}{\partial P_{i}}\) | \(H+\frac{\partial W_{2}}{\partial t}\) | ||
|
\(W_{3}\) 変数 \(\{p_{i}\}\), \(\{P_{i}\}\) |
\(W_{3}=W_{2}-\sum_{i}p_{i}q_{i}\) \(W_{3}=W_{1}+\sum_{i}P_{i}Q_{i}-\sum_{i}p_{i}q_{i}\) |
\(-\frac{\partial W_{3}}{\partial p_{i}}\) | \(\frac{\partial W_{3}}{\partial P_{i}}\) | \(H+\frac{\partial W_{3}}{\partial t}\) | ||
|
\(W_{4}\) 変数 \(\{p_{i}\}\), \(\{Q_{i}\}\) |
\(W_{4}=W_{3}-\sum_{i}P_{i}Q_{i}\) \(W_{4}=W_{1}-\sum_{i}p_{i}q_{i}\) |
\(-\frac{\partial W_{4}}{\partial p_{i}}\) | \(-\frac{\partial W_{4}}{\partial Q_{i}}\) | \(H+\frac{\partial W_{4}}{\partial t}\) | ||
このようにしてみると、正準変換後のハミルトニアン\({H}’\)は変数をどれを使っても(母関数をどれを使っても)変わらないことがわかります。
ということは、⑦式のように母関数\(W_{1}\)の変数を\(\{q_{i}\}\)と\(\{Q_{i}\}\)としましたが、上の変換公式に従いさえすれば母関数としては元の変数\(\{q_{i}\}\)と\(\{p_{i}\}\)から一組、新しい変数\(\{Q_{i}\}\)と\(\{P_{i}\}\)から一組選べば良いということになります。
感想
上のように表にまとめましたが、やっていることが別の分野でやったことがあるような感覚になりました。
・・・・
熱力学でも同じことをやったような気がします(統計力学でしたか?)
下記に書いている、\(U(S, V, N)\),\(H(S, p, N)\),\(F(T, V, N)\),\(G(T, p, N)\) が母関数\(W_{1}\),\(W_{2}\),\(W_{3}\),\(W_{4}\)に対応しているのだろうなと。
下記にこれらの関数を使った熱力学の概要を書いておきますが、数学的な手続きは全く同じでそうだとするならば、この母関数も話はここでは終わらず、熱力学でいうところのマクスウェルの関係式というのが解析力学にも登場するはずです。
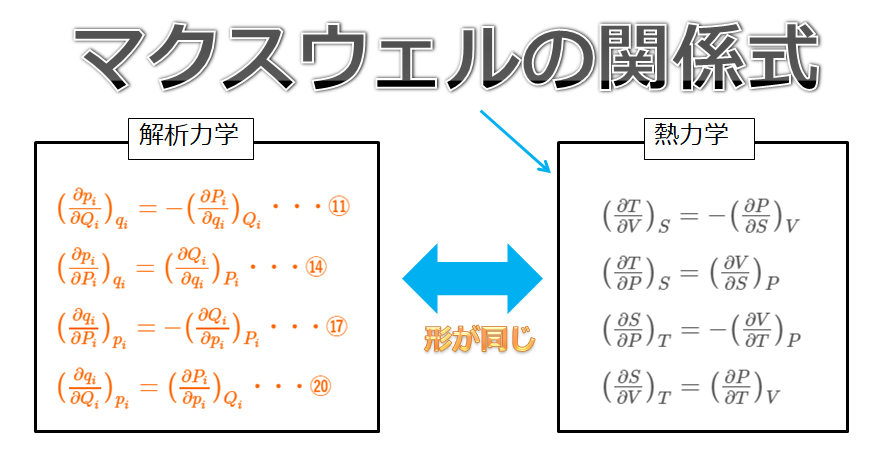
マクスウェルの関係式
次回は解析力学でも上記のような関係式を母関数から導こうと思います(^^)/
下記はちょっと余談(‘_’)
熱力学関数の概要
以下の熱力学的関数を変換する際にルジャンドル変換が使われます。
内部エネルギー:\(U(S, V, N)\)
エンタルピー :\(H(S, p, N)\)
ヘルムホルツの自由エネルギー :\(F(T, V, N)\)
ギブスの自由エネルギー:\(G(T, p, N)\)
\(V\):体積
\(P\):圧力
\(S\):エントロピー
\(T\):温度
内部エネルギーからエンタルピー
\(U(S,V)=H(S,P)-PV\)
or
\(H(S,P)=U(S,V)+PV\)
等圧条件下にある系で、吸熱すると内部のエネルギーと外部にする仕事を考えた熱力学の関数がエンタルピー\(H\)です。
内部エネルギーからヘルムホルトの自由エネルギーへ
\(F(T,V)=U(S,V)-TS\)
化学変化を含めた熱力学的系の等温過程において、系の最大仕事(潜在的な仕事能力)、自発的変化の方向、平衡条件などを表す指標となります。
温度が決定している状態で、系の平衡状態を決めるのは、内部エネルギー\(U\)が最小だけでは情報が足らず、エントロピー\(S\)(乱雑さ)も考慮して系の状態が決定される熱力学の関数がヘルムホルツの自由エネルギー\(F\)です。
例えば、温度が高い場合は式を見てお分かりのように、\(TS\)があるのでエントロピー\(S\)を大きくした方がヘルムホルツの自由エネルギー\(F\)は最小の方向に向かいますね。
だから、高温化では状態はランダム(激しく運動する)な方向に系が状態を取りたがるというような理解の仕方ができます。
ヘルムホルトの自由エネルギーからギブスの自由エネルギーへ
\(G(T,P)=F(T,V)+PV\)
等温等圧過程(容積が変化を考慮)の自由エネルギーを考えたい場合に威力を発揮する熱力学の関数がギブスの自由エネルギー\(G\)です。
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ランダウ力学
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。