いよいよ当ブログも、ポアッソンの括弧式について書くことができます。
しかし、詳しく書けるほど僕の理解が追い付いていません(*_*;
そこで、本記事はまずポアッソン式の定義を示し、そこから導出される定理をいくつか証明しながら理解を進めていきたいと考えています。
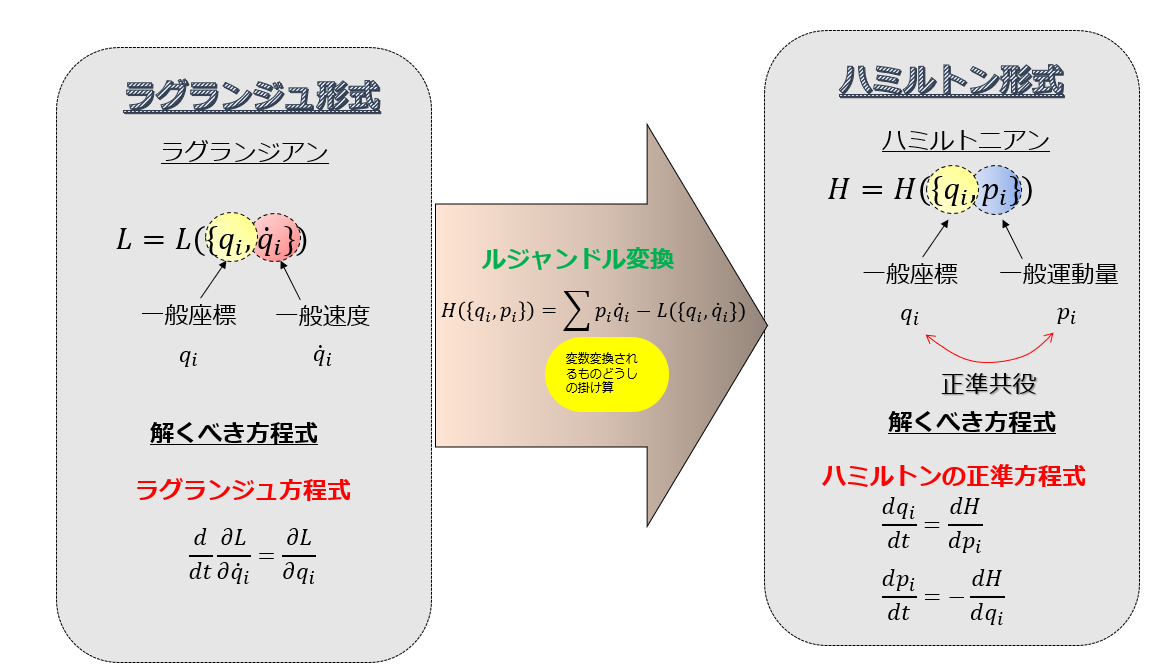
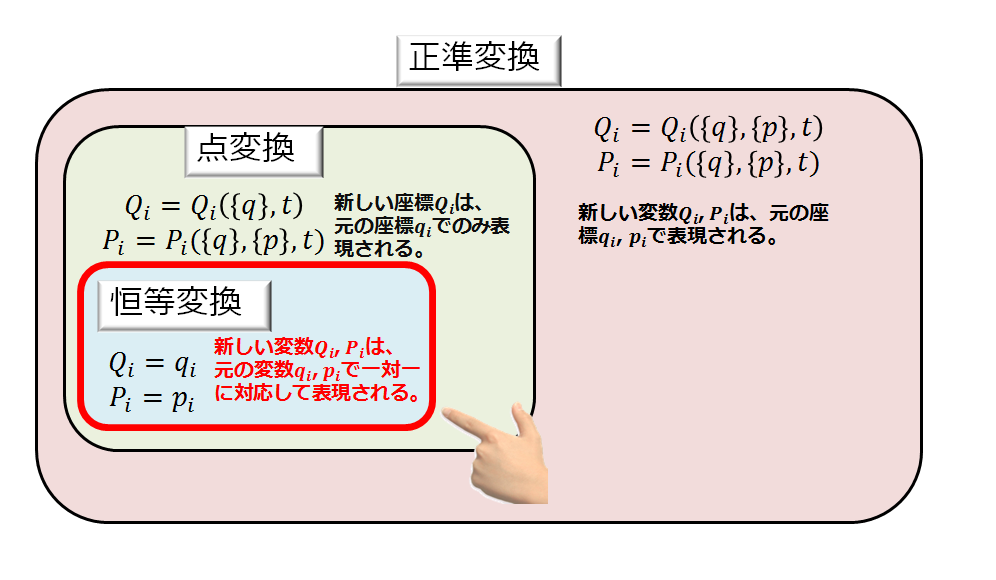
もちろん、解析力学ではハミルトンの正準方程式をみたすような変数変換、すなわち正準変換を考えたのですから、当然ポアッソンの括弧式においても正準変換に対してどうなのか?という考察や証明は着いて回るでしょう。
ポアッソン括弧式に関連した、紹介したい定理を示しておきます。
- ポアッソン括弧式の定義←本記事
- ポアンカレの定理
- 変数\(q_{i},p_{i}\)に対して、\(Q_{i},P_{i}\)が正準変換であるための必要十分条件は、
\(\{Q_{i},Q_{j}\}=0\)、\(\{P_{i},P_{j}\}=0\)、\(\{Q_{i},P_{j}\}=\delta _{ij}\)
である。- 正準変換に対して、ポアッソン括弧式は不変
- 量子力学とのつながり
ポアッソン括弧式の定義
まずは、ポアッソン括弧式の定義から入ろうと思います。
定義なので意味を考えずにとりあえずこのように書くと誰かが決めたので、それを覚えましょう(笑)
定義
\(\{q_{i}\},\{p_{i}\}\)を変数とする、関数\(f(\{q_{i}\},\{p_{i}\})\)と\(g(\{q_{i}\},\{p_{i}\})\)に対して、
\begin{align*}\{f,g\}_{q,p}=\sum_{i}\big( \frac{\partial f}{\partial q_{i}}\frac{\partial g}{\partial p_{i}}-\frac{\partial f}{\partial p_{i}}\frac{\partial g}{\partial q_{i}}\big)\cdot\cdot\cdot (1)\end{align*}
右辺の偏微分などを、左辺のような表記として書きます。
これを「ポアッソン括弧式」と呼びます。
ここまでは何も難しい話ではないでしょう。
ただ定義を書いただけですからね。
次に、なぜこのようなポアッソン括弧式というのを定義づけしたのか・・・・・・
それはさておき、どのような場面にポアッソン括弧式が登場するのか?を示したいと思います。
物理量\(f(\{q_{i}\},\{p_{i}\},t)\)の時間変化
ハミルトン形式では\(\{q_{i}\},\{p_{i}\}\)を変数として定めれば、<<力学的な状態>>というのが決められるわけですので、ある物理量\(f\)は当然それらの変数として決められるわけです。
ある物理量\(f\)は時間に陽に依存するとすれば、
と書けます。
そこで、僕たちが知りたいのは物理量\(f\)の時間変化ですので、これを時間微分してやります。
となります。
ここで、ハミルトンの正準方程式より、
です。
※さらっと書きましたが、復習したい方は↓下記をどうぞ。
【まとめ】ハミルトンの正準方程式の導出(第15報)
(3)(4)式を(2)式に代入します。
そうすると、「お!!第二項がポアッソン括弧式ではないか」となります(^^)/
ゆえに②式は、
と、こじんまりとまとまりましたね。
ハミルトニアンが時間変化しない場合は?
ハミルトニアンが時間に依存しない場合は、⑥式がどうなるのでしょうか??
ハミルトン形式では\(\{q_{i}\},\{p_{i}\}\)を変数とするときのエネルギーのことを特にハミルトニアンと呼んでいたのですから、ハミルトニアンが時間に依存しない場合というのはエネルギーの保存する場合は?ということになります。
その場合は、
となるので、
上式で、
と書いていたある物理量\(f\)を単にハミルトニアン\(H\)に置き換えるだけで定式化は完成しそうです。
(6)式の物理量\(f\)を\(H\)に置き換えると、
となります。
右辺の
とわかるので、ハミルトニアンが時間に依存しない場合は、
となります。
これを見ると、ハミルトニアンが時間に陽に依存しないときは、ハミルトンの時間変化そのものがないということが明らかです。
※ハミルトニアンが時間に陽に依存しないというのは、「ハミルトニアンの変数\(q_{i}\)、\(p_{i}\)は本当は時間に依存して変化するのですが、同じ\(q_{i}\)、\(p_{i}\)であるときに、ほっておいても(時間が変化しても)ハミルトニアンが変化することはない」という意味です。
実は、(7)式は一般的には自明ではないでしょう。
なぜなら、
ハミルトニアンの変数\(q_{i}\)、\(p_{i}\)、\(t\)は互いに独立としていますが、変数\(q_{i}\)、\(p_{i}\)も本当は時間によって変化するのですからそれに応じてハミルトニアン\(H\)も変化して良いように思えます。
でもよく考えたら、
ハミルトニアンの定式自体がエネルギー保存を意味しているわけでして、
ハミルトニアンが陽に依存するというのは、外から時間とともにエネルギーを注入もしくは放出しているのでその時点でエネルギーの保存は成り立たない
(すなわち⑦式の等式が成り立たない)ですよね。
反対に、外からエネルギーの注入もしくは放出がない、すなわちハミルトニアンが陽に時間に依存しないのであれば、定式通りハミルトニアンは時間に対して保存するでしょう。
すなわち(7)式に帰着します。
ポアソン括弧式の性質
性質と言うほどたいしたものではありません(笑)
ポアッソン括弧式の定義に従うと、
\begin{align*}\{f,g\}_{q,p}=\sum_{i}\big( \frac{\partial f}{\partial q_{i}}\frac{\partial g}{\partial p_{i}}-\frac{\partial f}{\partial p_{i}}\frac{\partial g}{\partial q_{i}}\big)\cdot\cdot\cdot (1)\end{align*}
ですので、下記の⑧⑨⑩式の関係式は覚えておきましょう(^^)/
代入すれば、すぐわかるので導出は省略しますので、ご興味ある方は手を動かしてみましょう♪
\(f=q_{i},g=q_{j}\)のとき
\(f=p_{i},g=p_{j}\)のとき
\(f=q_{i},g=p_{j}\)のとき
まとめ
時間に陽に依存するある物理量\(f\)を、
と書きます。
そのとき、物理量\(f\)の時間変化は、
と書けます。
ここで、下記のような表記の仕方を定義しました。
\begin{align*}\{f,g\}_{q,p}=\sum\big( \frac{\partial f}{\partial q_{i}}\frac{\partial g}{\partial p_{i}}-\frac{\partial f}{\partial p_{i}}\frac{\partial g}{\partial q_{i}}\big)\cdot\cdot\cdot (1)\end{align*}
これを「ポアッソン括弧式」と呼びます。
ポアッソン括弧式を使った関係式としては、
があります。
次回
次回は、
- ポアッソン括弧式の定義←本記事
- ポアンカレの定理←次回
- 変数\(\{q_{i}\},\{p_{i}\}\)に対して、\(\{Q_{i}\},\{P_{i}\}\)が正準変換であるための必要十分条件は、
\(\{Q_{i},Q_{j}\}=0\)、\(\{P_{i},P_{j}\}=0\)、\(\{Q_{i},P_{j}\}=\delta _{ij}\)
である。- 正準変換に対して、ポアッソン括弧式は不変
- 量子力学とのつながり
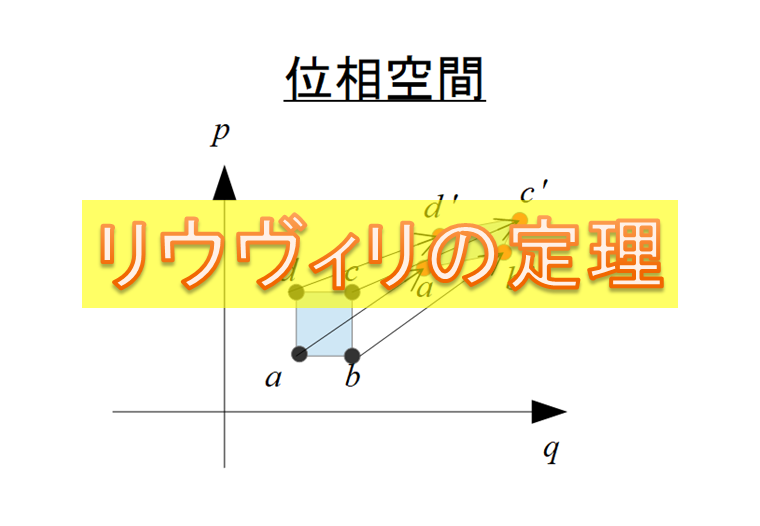
ポアンカレの定理は、リウヴィリの定理と意味合いは同じでしょう。きっと。。。。
リウビリの定理は↓こちらに書いておきました。
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ランダウ力学
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。