【まとめ】ハミルトンの正準方程式の導出

当ブログで、ハミルトンの正準方程式をいくつかの方法で導出したのでまとめておこうと思います。

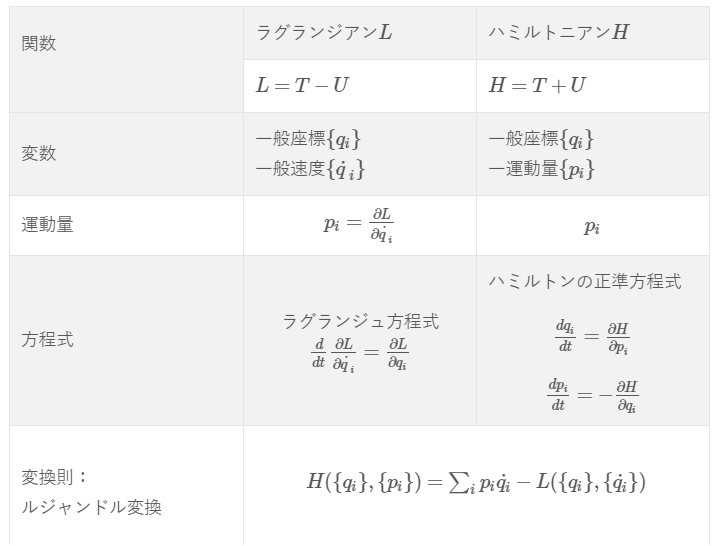
ハミルトンの正準方程式

ハミルトニアン\(H(\{q_{i}\},\{p_{i}\})\)に対して

\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (1)\end{align*}

\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (2)\end{align*}

<<力学的な状態>>を決めるのに変数を、一般座標\(q_{i}\)と一般運動量\(p_{i}\)を変数として、関数ハミルトニアン\(H(\{q_{i}\},\{p_{i}\})\)を作ります。

特に、座標\(q_{i}\)と運動量\(p_{i}\)を変数とする場合においてハミルトニアン\(H\)と言いますが、系のエネルギーと思ってよいです。

ハミルトニアン

\begin{align*}H=T+U\end{align*}

※運動エネルギー\(T(\{p_{i}\})=\sum_{i}\frac{1}{2}p_{i}^2\)
↑デカルト座標で考えるならば
※ポテンシャルエネルギー\(U(\{q{i}\})\)

このようにハミルトニアンを作って①②式に代入することで、系を記述する方程式（運動方程式）が導けます。

ハミルトンの正準方程式：まとめ

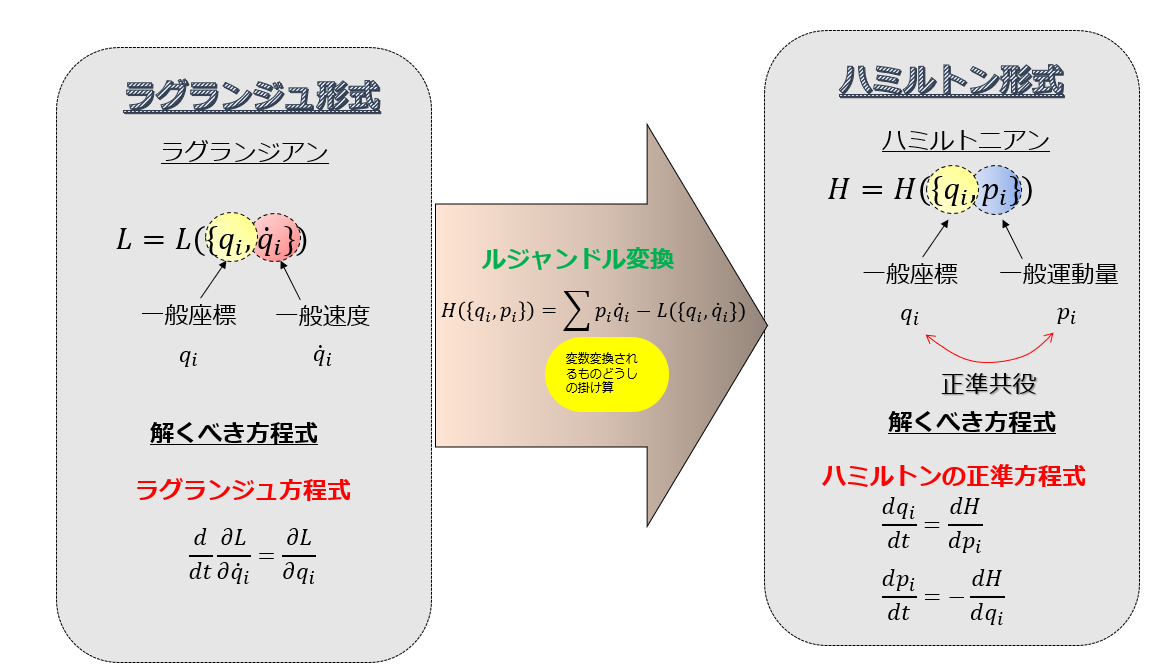
当ブログで3つの方法でハミルトンの正準方程式の導出を行いました。

導出方法	手続き
ルジャンドル変換を用いて導出 >>ルジャンドル変換からハミルトンの正準方程式の導出【補足説明】 >>ルジャンドル変換：イメージ図と利用例を挙げてみた >>ルジャンドル変換の導出：超簡単に導出	ルジャンドル変換 \(H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\) \(\dot{q_{i}}=\frac{\partial H}{\partial p_{i}}\) \(p_{i}=\frac{\partial L}{\partial \dot{q_{i}}}\) それぞれの変数は上記の関係があるとして①②式を導出 ↑途中でラグランジュ方程式ラグランジュ方程式：\(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial {q}_{i}}\)を使う。
ラグランジュ方程式から導出 >>ラグランジュ方程式からハミルトンの正準方程式の導出	ラグランジアン：\(L(\{q_{i}\},\{\dot{q}_{i}\})\) の全微分を考え、ラグランジュ方程式：\(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial {q}_{i}}\) >>最小作用の原理　ラグランジュ方程式の導出：ランダウ=リフシッツの”力学”　わかりやすく解説が成り立つとして①②式を導出 ※運動量：\(p_{i}=\frac{\partial L}{\partial \dot{q}_{i}}\) >>運動量保存則：並進対称（ネーターの定理）：ランダウ=リフシッツの”力学”
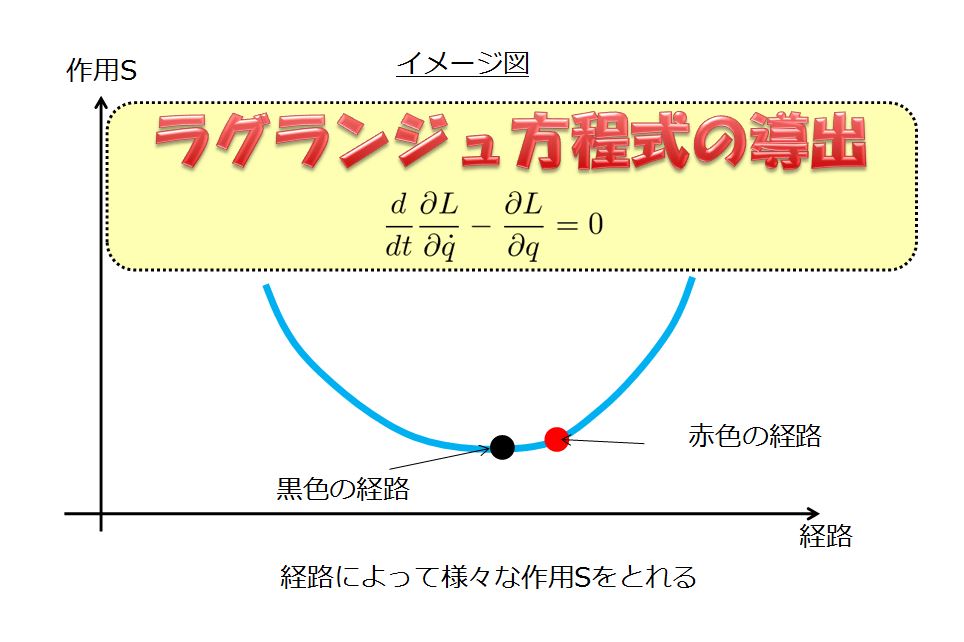
最小作用の原理から導出 >>最小作用の原理からハミルトンの正準方程式の導出	作用\(S\)はが停留点をとっているとき、 \(\delta S=0\) すなわち \(\int_{t_{1}}^{t_{2}}\big(L(\{q_{i}+\delta{q_{i}}\},\{\dot{q}_{i}+\delta{\dot{q}_{i}}\},t)-L(\{q_{i}\},\{\dot{q}_{i}\},t)\big)dt=0\) にルジャンドル変換 \(H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\) を代入して①②式を導出