こんにちは(@t_kun_kamakiri)。
本記事では、熱力学第一法則の説明をします。
「熱力学第一法則」と「状態方程式」を用いて熱力学を理解することを目的とします。
熱力学第一法則
熱力学第一法則は、数式で書くと
であります。
※\(d^{\prime}Q=dU+d^{\prime}W\)は教科書では「状態量」と「状態量でないもの」を区別するために「$\prime$(プライム)」をつけて区別する場合があります。
「$\prime$(プライム)を付けたものは」状態量ではないということを明記することがあります。
熱力学第一法則に関する下記の関連記事もどうぞ。
熱力学第一法則はエネルギーの保存則である
熱力学第一法則は、超ざっくり言ってしまえば「エネルギーの保存則」を言っているに過ぎません。
すなわち、
「外部から与えられた熱量」=「内部エネルギー」+「外へする仕事」
と言っているです。
絵で見るとこんな感じです。
外から与えられたエネルギー\(d^{\prime}Q\)
これは外から与えられた熱的なエネルギーで、「入ってくる熱量」も「失う熱量」も込みで考えています。

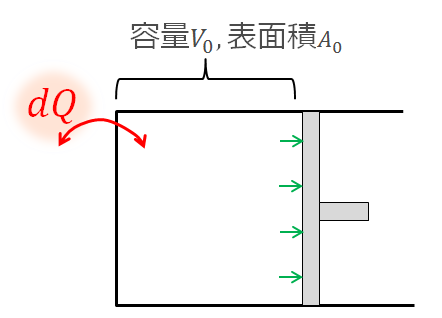
なんにも難しいことではないですね。
内部エネルギー
「内部エネルギー」と言われてもピンとこないでしょう。
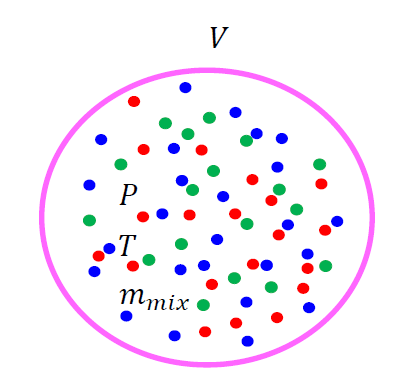
具体的に言えば、内部エネルギー、すなわち内部の状態とは、温度\(T\)、圧力\(P\)、体積\(V\)などの状態量のことを指します。

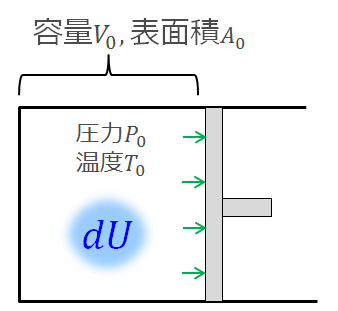
この内部エネルギーとかいうやつ・・・・・とても曖昧な感じがしませんか?
それについては、後で詳しくお話しします。
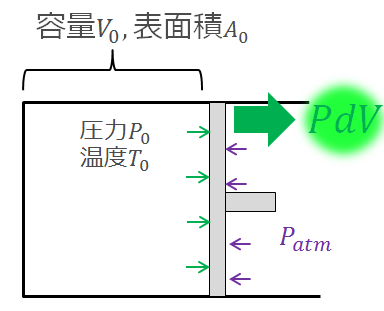
外へする仕事
これは閉じた空間内にある内部状態(温度、圧力)などを使って、力学的に「力×距離」で仕事をするということを意味しています。

ここまで、内部状態という曖昧な言葉を乱用しました(笑)
一体、「内部エネルギー」とは何でしょうか?
内部エネルギーとは
内部状態の説明をもう一度書きますが、具体的に言えば、内部エネルギー、すなわち内部の状態とは、温度\(T\)、圧力\(P\)、体積\(V\)などの状態量のことを指します。
それでも曖昧さな表現ですよね?
なぜ曖昧さが残るのでしょう?
だいたい温度とか圧力とか実態は何なのか説明していないからですよね。
そこを話さなければならない気がします。
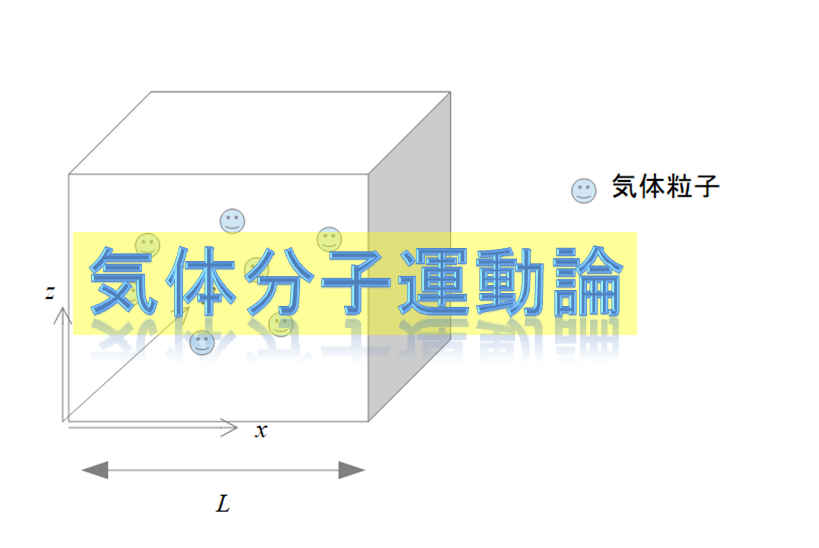
話し出すと長くなるので、簡単に言えば、「気体分子運動論」によると、
これらを内部的な状態として、人が観測するのです。
※ちなみに気体分子運動論は下記の記事に書きました。
しかし、これが熱力学のミクロな解釈と考えてはいけません。あくまで理想気体での力学的な運動を考えた時に下記の記事のような内容になるという解釈であることを覚えておかなくてはいけません。
ところで、この気体分子運動をもとに考えるならば、観測で得た圧力や温度は本質的には同じものを測っているようにも思えます。
”同じもの”という意味は、同じものを測定しているという意味ではありません。
片方がわかれば、片方は理論的に計算できるという意味です。
なぜなら熱力学的な状態は、温度\(T\)、圧力\(p\)、体積\(V\)などの独立な2つの変数さえ指定すれば、状態は決定されるのです。
(もっと言えば圧力は力学的な「単位面積当たりの圧力」という解釈でも可能ですが、温度というのは人間が測定結果として数値で表した概念のようなものです。)
例えば、視覚的に考えやすい体積\(V\)(閉じた空間)を変数として選ぶとすれば、あとひとつを状態変数として選択すれば、考えるべき状態と言うのは決定されます。
だから、仮に圧力\(p\)を観測すれば(変数として選択すれば)、温度\(T\)は測定しなくても「測定したと圧力\(p\)と体積\(V\)」とを熱力学的な関係式から決定することができるのです。
では、その温度\(T\)は体積\(V\)と圧力\(p\)との関係式とは、なんでしょうか?
それは、、熱力学的な状態関数は、
として関係式のことです。
お分かりでしょうが、温度\(T\)、圧力\(p\)、体積\(V\)などの独立な2つの変数さえ指定すれば良いと言った意味は(2)式のような関係式があるために、
未知数:3つ
式:1つ
なので、未知数を2つ指定すれば問題は解けるということを言いたいのだ。
さて、ここで
とは具体的には何でしょうか?
具体的な内容は、こちらの記事を参考で書いております。