エンタルピーを用いてベルヌーイの定理を記述

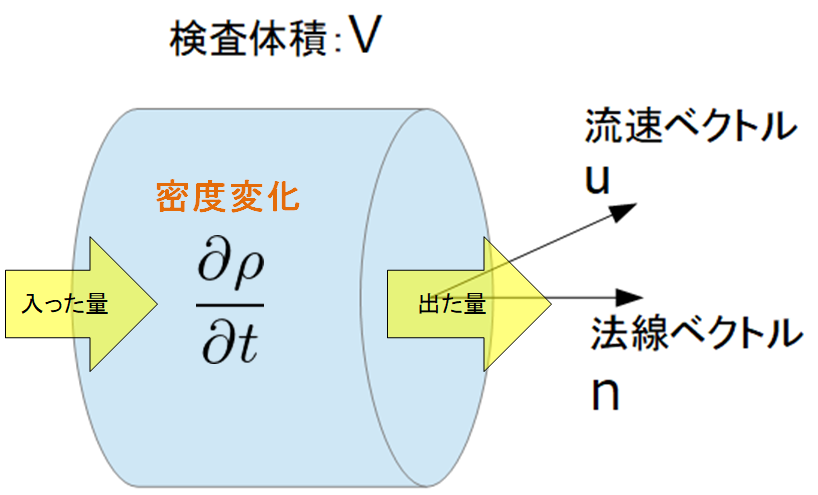
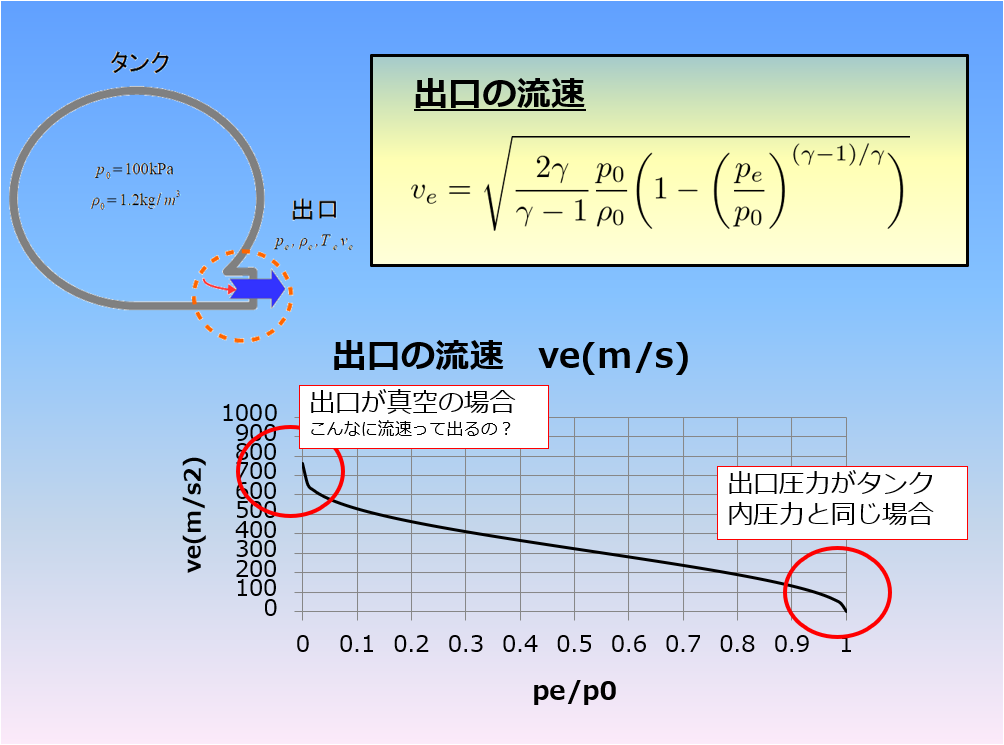
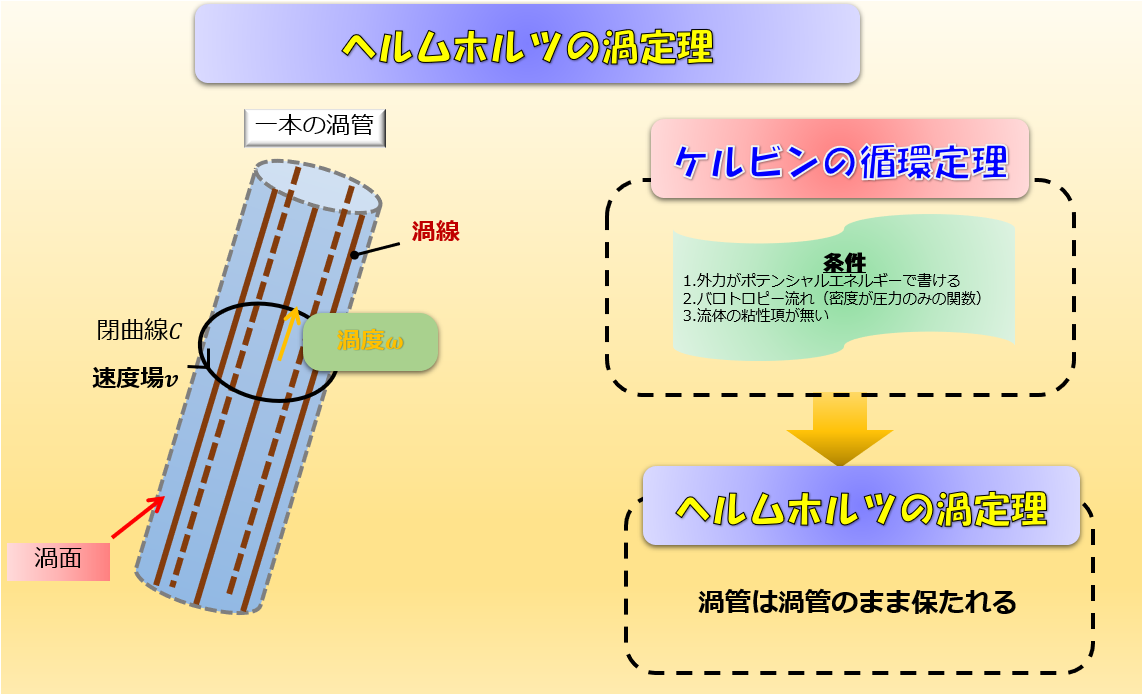
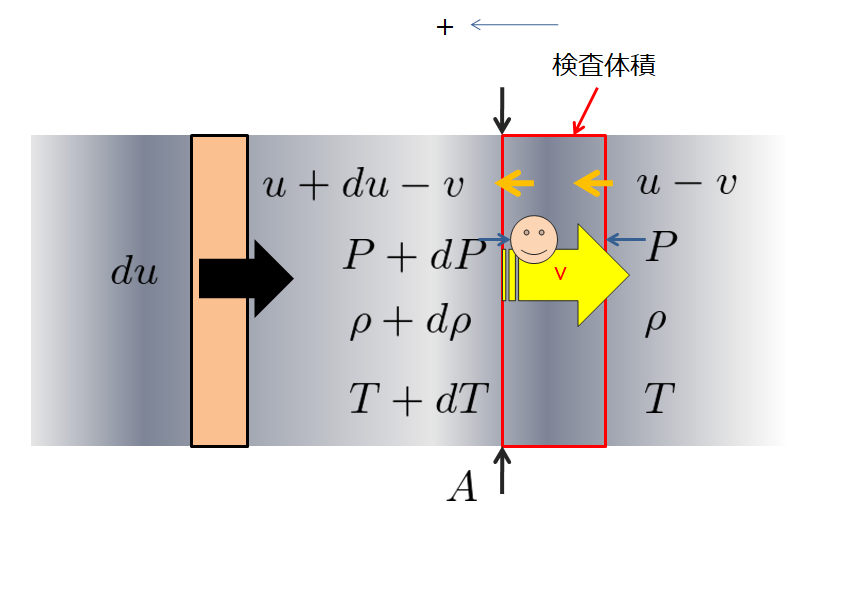
さて、前回の記事の続きをやっていきます。

前回の記事はこちら

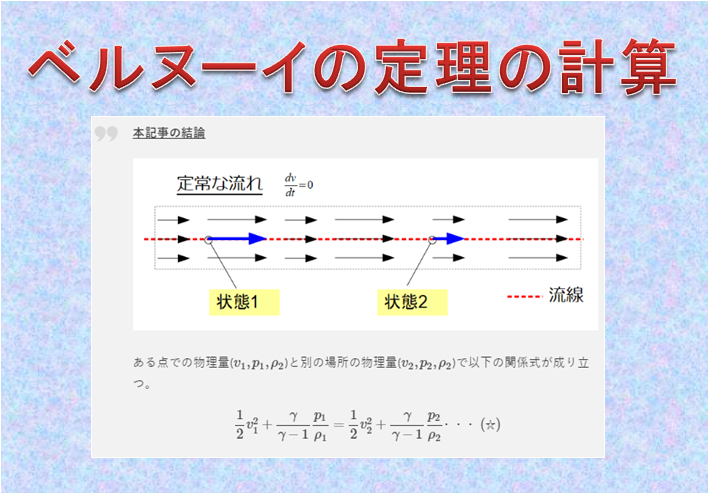
この記事で出た結論は、こんな感じでした。

ある点での物理量(\(v_{1},p_{1},\rho_{2}\))と別の場所の物理量(\(v_{2},p_{2},\rho_{2}\))で以下の関係式が成り立つ。

\begin{align*}
\frac{1}{2}v_{1}^2+\frac{\gamma}{\gamma-1}\frac{p_{1}}{\rho_{1}}=\frac{1}{2}v_{2}^2+\frac{\gamma}{\gamma-1}\frac{p_{2}}{\rho_{2}}\cdot\cdot\cdot (\diamondsuit)
\end{align*}

【仮定】
・1次元
・非粘性
・非定常
・等エントロピー流れ（断熱過程）
・理想気体

（\(\diamondsuit\)）式の右辺と左辺の第二項はちょっと覚えづらいですね。

この第二項はエンタルピーというのを導入すれば、シンンプルに、

\begin{align*}
\frac{1}{2}v_{1}^2+h_{1}=\frac{1}{2}v_{2}^2+h_{2}\cdot\cdot\cdot (\diamondsuit\diamondsuit)
\end{align*}

あるいは、

\begin{align*}
\frac{1}{2}v_{1}^2+C_{p}T_{1}=\frac{1}{2}v_{2}^2+C_{p}T_{2}
\cdot\cdot\cdot (\diamondsuit\diamondsuit\diamondsuit)
\end{align*}

と書けます。

本記事では(\(\diamondsuit\diamondsuit\))や（\(\diamondsuit\diamondsuit\diamondsuit\)）までの導出についてまとめたいと思います。

エンタルピーとは
ルジャンドル変換を用いて内部エネルギーをエンタルピーへ変換
1. 解析力学でもルジャンドル変換
2. 熱力学でもルジャンドル変換
ベルヌーイの定理にエンタルピー\(h\)を導入
(8)式をベルヌーイの定理に代入
エンタルピー\(h\)を定圧比熱を用いて表記
まとめ

エンタルピーとは

エンタルピーの定義は、

\begin{align*}
H=U+pV
\end{align*}

\(U\)：内部エネルギー
\(p\)：圧力
\(V\)：体積

と言ってしまえばそこまでなのですが、少しだけ意味を書いていおきます。
（そんなに詳しく書けないですが）

ちなみに、エンタルピーの定義は、単位粒子当たり（あるいは単位質量当たり）として、

\begin{align*}
h=u+pv
\end{align*}

と、示量変数を小文字で書いて考える場合もあります。

この場合の、示量変数はエンタルピー\(h\)、体積\(v\)です。
※圧力\(p\)も小文字で書いていますが、大文字で書くのが面倒なだけで、決して単位粒子あたりの圧力と考えてはいけません。（圧力は示強変数です）

熱力学の状態を決定するのに、基本関係式としてエントロピー\(S\)で表示しても良いし、内部エネルギー\(U\)で表示しても良いのです。

それぞれ変数として、

エントロピー：\(S(U,V,N)\)

内部エネルギー：\(U(S,V,N)\)

と、括弧内の変数を持っているというふうに書きます。

ここで、「エントロピーなんてあまり馴染みがないから、内部エネルギーでも使って考えるかー」ってなったとして、内部エネルギーで考えるとします。

その時の変数は、エントロピー\(S\)と\(体積\)と粒子数\(N\)ですね。

しかし、内部エネルギーもエントロピー\(S\)も\(体積\)も示量変数だから、単位粒子当たり（あるいは単位質量あたり）で考えても良いことになります。

よって、

\begin{align*}
内部エネルギー：u(s,v)
\end{align*}

と書けます。

このようにして熱力学では変数２つを決めれば内部状態が定まり、熱力学的状態というのが決定できます。

今、変数は単位粒子当たりのエントロピー\(s\)と単位粒子当たりの体積としていますが、この変数は考えている系に応じて当然考えやすい変数を選択する方が賢い方法であると言えます。

例えば変数を体積\(v\)ではなく圧力\(p\)に変えて考えたい場合は、ルジャンドル変換により内部エネルギー\(u\)から新しい熱力学関数を作ることができます。

それがエンタルピーになります。

変数を圧力に変えることができれば、うれしいのは圧力一定の場合ですよね。

そうすると、圧力は変数でなくなるので、変数はたったひとつになります。

ルジャンドル変換を用いて内部エネルギーをエンタルピーへ変換

上で色々と言いましたが、早い話が「変数を体積から圧力に変えたい」ということです。

その変数変換のためにルジャンドル変換というのをするのですが、ルジャンドル変換は下記の記事で書きましたのでご参考ください。

解析力学でもルジャンドル変換

あるいは解析力学と学んだ際に、「ラグランジアン\(L\)からハミルトニアン\(H\)への変換」とか習った人がいればその対応関係からも理解できるかと思います。

こんな感じで、「ラグランジアン\(L\)として持っていた変数（一般座標\(q\)と一般速度\(\dot{q}\)」から「変数（一般座標\(q\)と一般運動量\(p\)を変数にもつハミルトニアン」への変換とかができます

※詳しくはこちら（解析力学）を参考にしてください。

熱力学でもルジャンドル変換

上記のような解析力学での対応関係で、熱力学でも「内部エネルギー\(u\)として持っていた変数（エントロピー\(s\)と体積\(v\)」から「変数（エントロピー\(s\)と圧力\(p\)を変数にもつエンタルピー」への変換が可能です。

こんな感じで新しい関数エンタルピー\(h\)を作ることができました。

※解析力学での運動量の変数を\(p\)と書いたり、ハミルトニアンを\(H\)と書いたり、熱力学で使っている文字と同じなのでややこしいですがご了承ください。

そういえば、一応言っておかないと(‘;’)

熱力学を勉強した方は、

\begin{align*}
p=-\bigg(\frac{\partial U}{\partial V}\bigg)_{S}・・・(1)
\end{align*}

というのを知っていると思います。

これはエントロピーを一定に保った場合(断熱）での関係式です。

この時に内部エネルギーの変数はエントロピーと体積です。

では、内部エネルギー\(U(T,V)\)のように変数を温度\(T\)と体積\(V\)で表記している場合もあるでしょう。

その時に、内部エネルギーを体積で偏微分すると上式のように、

\begin{align*}
p=-\bigg(\frac{\partial U}{\partial V}\bigg)_{T}
\end{align*}

なのでしたっけ？

・・・・・

答えは、

\begin{align*}
p=-\bigg(\frac{\partial U}{\partial V}\bigg)_{T}+T\bigg(\frac{\partial S}{\partial V}\bigg)_{T}・・・(2)
\end{align*}

となります。

これは先ほど違って、「温度を固定した場合の関係式です」ので、温度を一定に保つために熱が必要なので(1)にプラスして(2)の第二項のような項が付け加わります。

このように何を変数にして何を固定して偏微分しているのかというのはとても注意深く考えなくてはいけません。

こういった点がわかりにくいために、熱力学が苦手とされているのでしょうね。

完全な余談でした(‘;’)

ベルヌーイの定理にエンタルピー\(h\)を導入

では本題に入ります。

単位粒子当たり（単位質量あたりの）エンタルピー\(h\)は、

\begin{align*}
h=u+pv・・・(3)
\end{align*}

と書けます。

変数を明示的に書いておくと、

\begin{align*}
h(s,p)=u(s,v)+pv
\end{align*}

では、これを全微分します。

\begin{align*}
dh=du+pdv+vdp・・・(4)
\end{align*}

ここで、熱力学第一法則より、

\begin{align*}
dq=du+pdv・・・(5)
\end{align*}

でありますが（これも単位粒子当たり（単位質量あたり）として書いています）、今考えているのは等エントロピー過程であるので、

\begin{align*}
dq=0
\end{align*}

となります。

そうすると(4)式は、

\begin{align*}
dh=vdp・・・(6)
\end{align*}

となります。

ここで、体積\(v\)は「単位粒子当たり（単位質量あたり）の体積」なので、数密度（あるいは質量密度）で書くことができます。

\begin{align*}
\rho =\frac{1}{v}・・・(7)
\end{align*}

↑こんな感じです。

だから(6)式は、

\begin{align*}
dh=\frac{dp}{\rho}
\end{align*}

となります。

余談ですが、圧力一定下で問題を考えている場合は、\(dp=0\)だからエンタルピー\(h\)は変化しないですよね。

だから、

\begin{align*}
h=u+pv=const
\end{align*}

ってことになります。

(8)式をベルヌーイの定理に代入

(8)式はどこかで見たな？ってなるのです。

ベルヌーイの定理

\begin{align*}
\frac{1}{2}v^2+\int \frac{1}{\rho}dp=const
\end{align*}

の積分の中身です。

つまり積分の中身を(8)式に置き換えると、

\begin{align*}
\frac{1}{2}v^2+\int dh=const・・・(9)
\end{align*}

となるので、

\begin{align*}
\frac{1}{2}v^2+h=const・・・(10)
\end{align*}

となります。

えらくあっさりしましたが、冒頭で紹介した

\begin{align*}
\frac{1}{2}v_{1}^2+\frac{\gamma}{\gamma-1}\frac{p_{1}}{\rho_{1}}=\frac{1}{2}v_{2}^2+\frac{\gamma}{\gamma-1}\frac{p_{2}}{\rho_{2}}\cdot\cdot\cdot (\diamondsuit)
\end{align*}

と(10)式は同じなんですよね。

ベルヌーイの定理が下記のように書けて、

ベルヌーイの定理

\begin{align*}
\frac{1}{2}v^2+\int \frac{1}{\rho}dp=const
\end{align*}

【仮定】

1次元
非粘性
定常流れ

ここまでは上記のような仮定しか用いていないですが、ここに「等エントロピー流れ（断熱過程）」を仮定すると、（\(\diamondsuit\))であったり(10)式が導けたわけです。

見た目は変わっても同じベースの式から同じ仮定を用いて導出された2つの式は当然同じですよね。

エンタルピー\(h\)を定圧比熱を用いて表記

ベルヌーイの定理として(10)式を用いて考察しても良いですが、エンタルピー\(h\)ってだいたいどうやって扱うんだってなりませんかね。

そうした場合に「エンタルピー\(h\)を定圧比熱\(C_{p}\)で表記する」方法があるので、紹介だけしておきます。

導出方法はこちらに詳しく書いていますのでご参考ください。

まとめ

ある点での物理量(\(v_{1},p_{1},\rho_{2}\))と別の場所の物理量(\(v_{2},p_{2},\rho_{2}\))で以下の関係式が成り立つ。
【仮定】
・1次元
・非粘性
・非定常
・等エントロピー流れ（断熱過程）
・理想気体

このような状況を考えた時に、

\begin{align*}
\frac{1}{2}v_{1}^2+\frac{\gamma}{\gamma-1}\frac{p_{1}}{\rho_{1}}=\frac{1}{2}v_{2}^2+\frac{\gamma}{\gamma-1}\frac{p_{2}}{\rho_{2}}\cdot\cdot\cdot (\diamondsuit)
\end{align*}

と書いても良いし、

\begin{align*}
\frac{1}{2}v^2+h=const・・・(10)
\end{align*}

※エンタルピー\(h\)：\(h=u+pv\)

とも書いても良いし、

\begin{align*}
\frac{1}{2}v^2+C_{p}T=const・・・(11)
\end{align*}

とも書いても良い。

だから、(10)式を用いるのであれば、

\begin{align*}
\frac{1}{2}v_{1}^2+h_{1}=\frac{1}{2}v_{2}^2+h_{2}\cdot\cdot\cdot (\diamondsuit\diamondsuit)
\end{align*}

となりますし、(11)式を用いるならば、

\begin{align*}
\frac{1}{2}v_{1}^2+C_{p}T_{1}=\frac{1}{2}v_{2}^2+C_{p}T_{2}\cdot\cdot\cdot (\diamondsuit\diamondsuit\diamondsuit)
\end{align*}

となります。