こんにちは(^^)/
前回は、流体力学における循環というものを定義しました。
循環の定義については下記の記事を参考にしてください。
なぜ、このような記事を書いたのかと言いますと、
下記のような疑問に対してヒントを得るためです。
- なぜ渦が生成されるのか?
- 渦を生成する要因は何か?これらの”渦が生成するためのヒント”をいくつか与えられたらなと思います。
※完全なメカニズムまでは説明しきれないですが。
渦が生成するための仕組みを理解するために、以下の内容を順番に投稿していきたいと思います。
- 流体力学の循環の定義
- ケルビンの循環定理←本記事の内容
- ヘルムホルツの渦定理
- ラグランジュの渦定理
- ケルビンの循環定理を破る例(量子流体を例にする)
渦ができる要因は何かと考えるのも良いですが、逆に渦ができない条件ってあるのか?・・・・
どんな条件を課すと渦が生成しないのかを考えることも有益な情報を得ることができそうですよね。
というわけで、そのような内容と関連しているのが、本記事の内容で・・・ケルビンの循環定理というやつです(^^)/
復習:循環とはなんだったか?
流体力学の循環の定義を今一度復習しておきます。
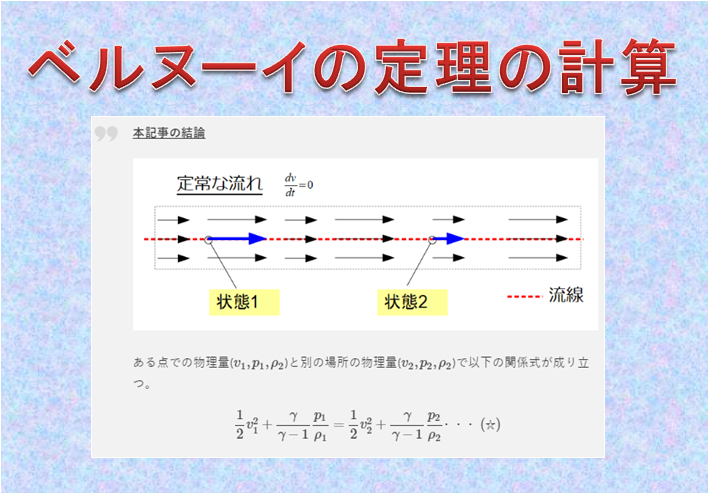
流れがあるところに閉曲線\(C\)を適当に作り、流速の速度場で一周線積分したもの(循環)というものを定義します。
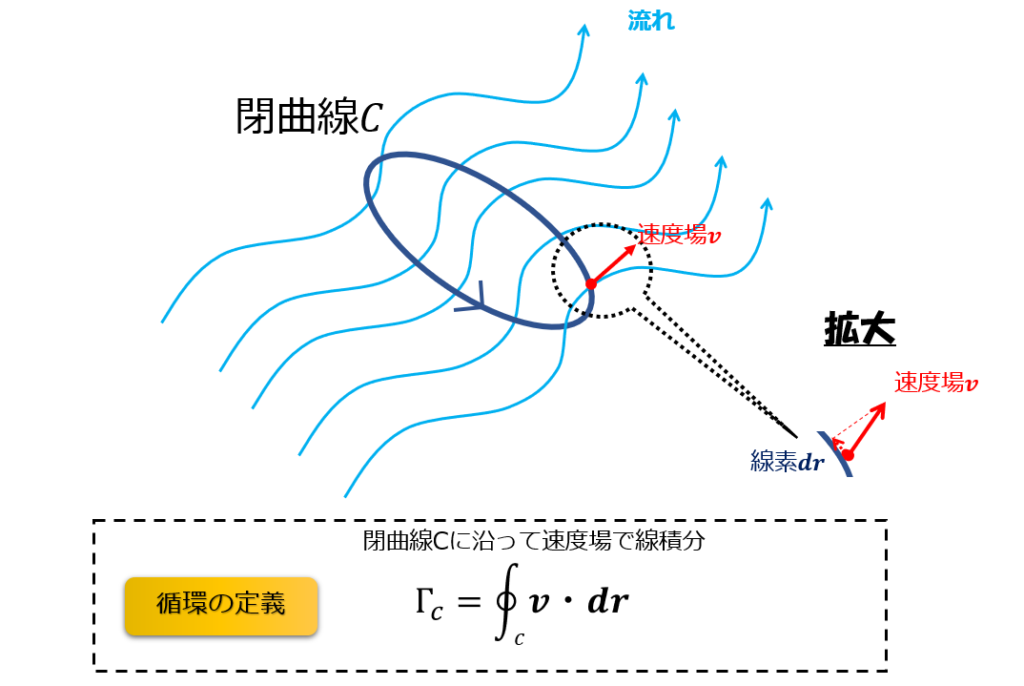

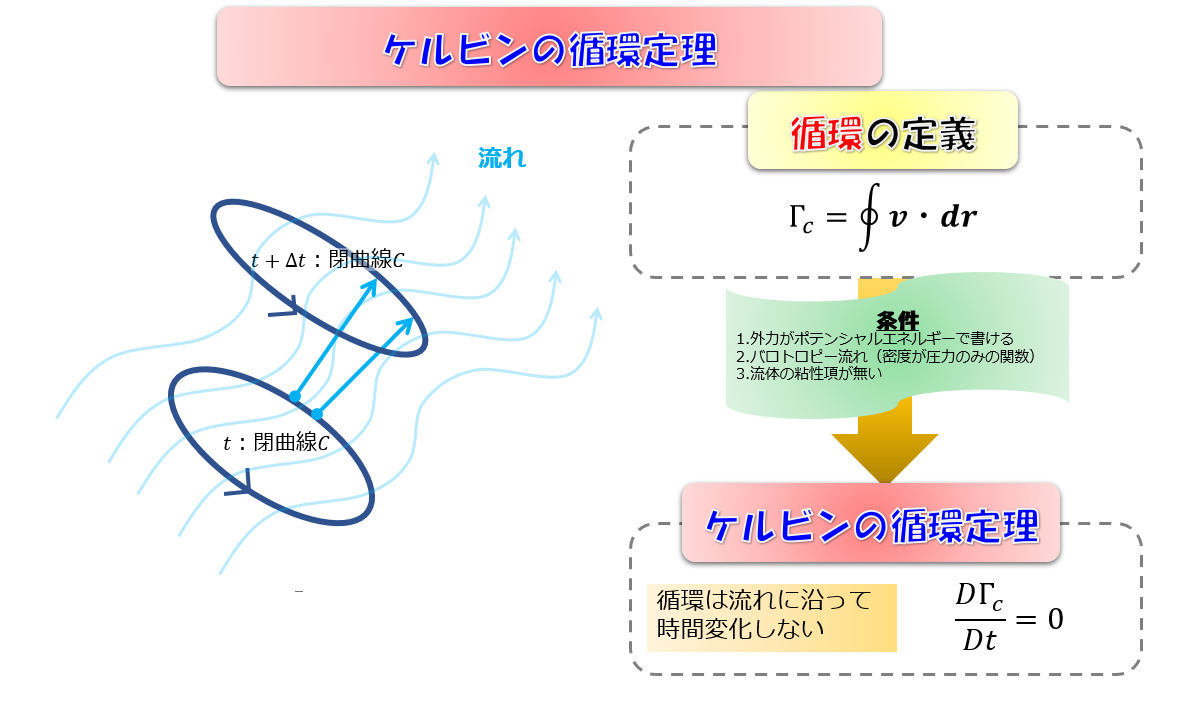
循環の定義
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}\tag{1}
\end{align*}
これが循環の定義です(^^)/
前回の記事でも書きましたが、循環はストークスの定理を使うことで、以下のように書き替えることができます。
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=\iint_{S}\bigg(\nabla\times \boldsymbol{v} \bigg)\cdot\boldsymbol{n}dS\tag{2}
\end{align*}
とこうなります。
\(\nabla\times\boldsymbol{v}=\boldsymbol{\omega}\)が渦度\(\boldsymbol{\omega}\)の定義なので、
循環は渦度を使って、
\Gamma_{c}=\iint_{S}\boldsymbol{\omega}\cdot\boldsymbol{n}dS\tag{3}
\end{align*}
となります。
これをマンガちっくに書くと・・・
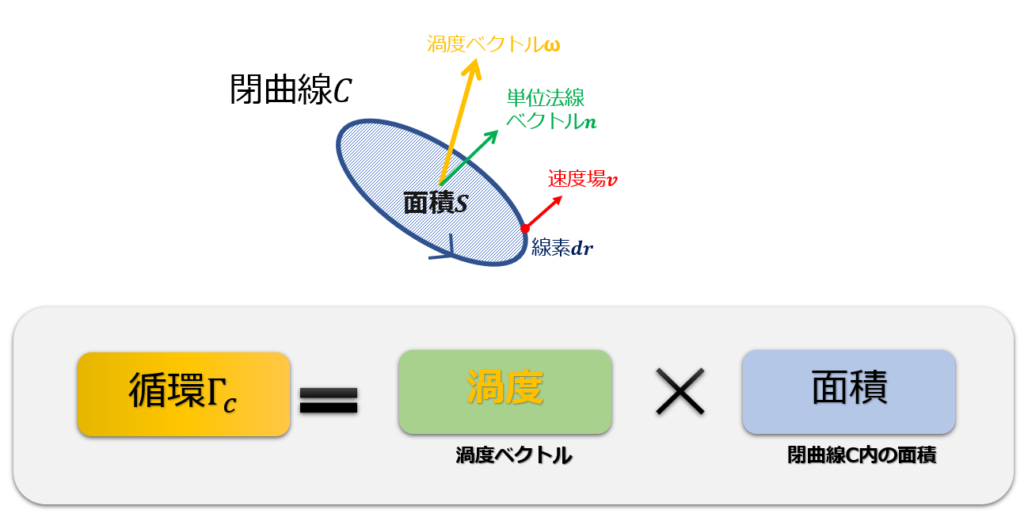

こんな感じです。
循環は、「渦度」と「閉曲線で囲まれた面積」との掛け算ということになります。
同じ面積でも、渦度ベクトルが大きな値を持っていると、循環は大きくなります。
なので、循環は渦度の強さを表現している量であるとも見ることができます。
ケルビンの循環定理とは?
ケルビンの循環定理の証明の計算をしていくのですが、ケルビンの循環定理とは何かということを押さえておきましょう。
下記のような、ある時刻\(t\)のひとつの閉曲線\(C\)での循環\(\Gamma_{c}(t)\)を考えます。
その閉曲線\(C\)が流れに沿って時間的にどのように変化するのかを考えます。
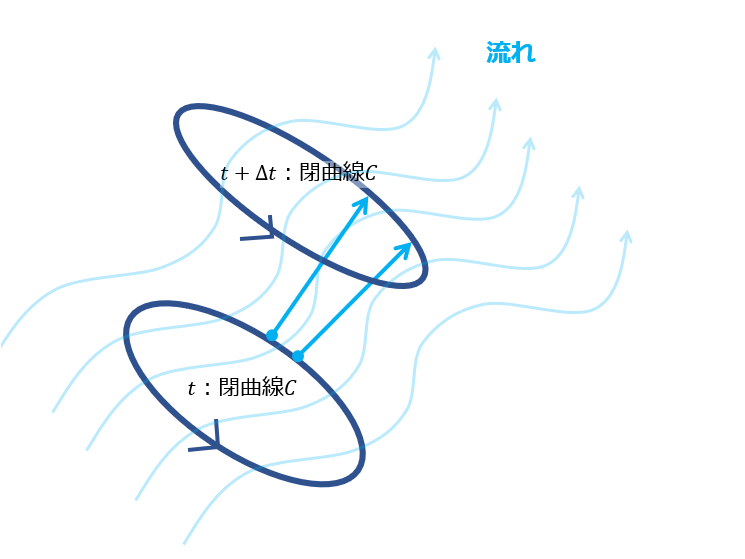



時刻\(t+\Delta t\)のときの循環\(\Gamma_{c}(t+\Delta t)\)を考えると、ある条件下においては、
\Gamma_{c}(t)=\Gamma_{c}(t+\Delta t)
\end{align*}
となるのです。
つまり、ある条件下において、循環は流れにそって時間変化 しないということが示すことができます。
そのある条件下とは何か?
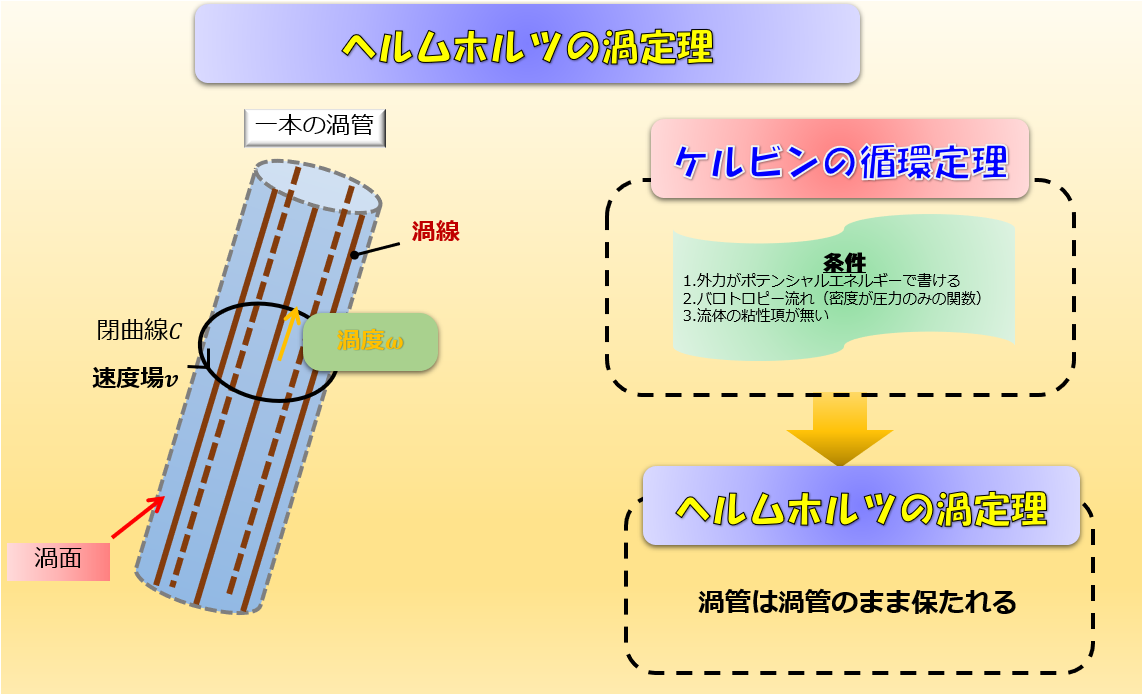
これらの3つの条件を課すことで、循環は流れにそって時間変化しないということを示すことができます。
これがケルビンの循環定理と呼ばれるものです。
上記の3つの条件はケルビンの循環定理の証明にはとても重要ですので、覚えておいてください(^^)/
流れに沿って時間変化する循環
ケルビンの循環定理の説明には、まず流れに沿って変化する循環の時間変化を考えるところからスタートします。




流体力学での時間変化というのは、\(\frac{d}{dt}\)で書くような時間微分ではなくて、流れ(流速\(\boldsymbol{v}\))に沿って時間変化する場として考えないといけなかったのですよね。
それは、物質微分です。
\frac{D}{Dt}=\frac{\partial }{\partial t}+\big(\boldsymbol{v}\cdot\nabla\big)\tag{4}
\end{align*}
と書きます。
※物質微分については、別途記事を追加しますm(_ _)m
※物質微分がややこしくて理解していないという方は、閉曲線を直線に置き換え、さらに線素を離散化し、線積分を和で表現すると理解できると思います。
(別途記事を追加します)
では、
流れに沿って変化する循環の時間変化を考えてみましょう。
循環\(\Gamma_{c}\)を物質微分してやります。
\frac{D\Gamma_{c}}{Dt}=\frac{D}{Dt}\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}\tag{5}
\end{align*}
ここで、線積分と物質微分を入れ替えます。
おいおい、積分と微分を入れ替えても良いのか!!となるかもしれませんが、後半の内容で示しているように、線素を離散化して考えるならば、「微分とΣは入れ替えてもよい」ので、ここでも積分と微分は入れ替えても良いと考えてよいでしょう(^^)/
例えば、下記のような簡単な例を見るとイメージができると思います。
\frac{d}{dt}\Sigma_{i=1}^{3}x_{i}(t)=\frac{d}{dt}\big(x_{1}(t)+x_{2}(t)+x_{3}(t)\big)=\Sigma_{i=1}^{3}\frac{d}{dt}x_{i}(t)
\end{align*}
積分と和が入れ替わりました。
気を取り直して、線積分と物質微分を入れ替えます。
\frac{D}{Dt}\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=\oint_{c} \frac{D}{Dt}\bigg(\boldsymbol{v} \cdot d\boldsymbol{r}\bigg)\tag{6}
\end{align*}
このようになると、線積分の中身をひとつひとつ分解していけば良いです。
線積分の中
\frac{D}{Dt}\bigg(\boldsymbol{v} \cdot d\boldsymbol{r}\bigg)=\frac{D\boldsymbol{v}}{Dt}\cdot d\boldsymbol{r}+\boldsymbol{v} \cdot\frac{D d\boldsymbol{r}}{Dt}\tag{7}
\end{align*}
これで、流れに沿って時間変化する循環を書くことができました。
さらに、意味を考えていくべく・・・・
ここで一旦(7)式を目に焼き付けておきます(‘ω’)
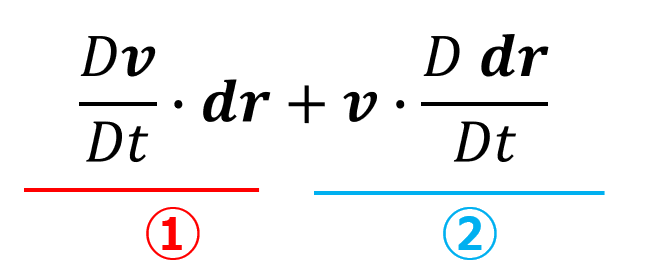
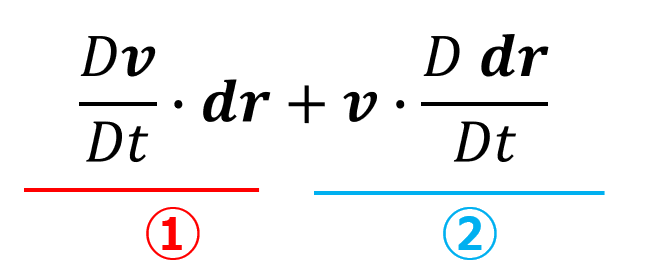
①の項について
(7)式の第一項の\(\frac{D\boldsymbol{v}}{Dt}\cdot d\boldsymbol{r}\)は、以下のように書くことができます。
\frac{D\boldsymbol{v}}{Dt}\cdot d\boldsymbol{r}=\frac{\partial \boldsymbol{v}}{\partial t}+\big(\boldsymbol{v}\cdot \nabla\big)\boldsymbol{v}\tag{8}
\end{align*}
これは、流れに沿って時間変化する速度を意味していますよね。
つまり、流体力学の基礎方程式のひとつ・・・ナビエストークス方程式です。
ナビエストークス方程式
\frac{\partial \boldsymbol{v}}{\partial t}+\big(\boldsymbol{v}\cdot \nabla\big)\boldsymbol{v}=-\frac{1}{\rho }\nabla p+\nu\nabla^{2}\boldsymbol{v}+\boldsymbol{K}\tag{8}
\end{align*}
※\(\boldsymbol{K}\):外力
ここで、以下の条件を課してみましょう。
ナビエストークス方程式の右辺、
- 第一項:\(-\frac{1}{\rho }\nabla p=-\nabla P\)と書ける\(P(p)\)を用意:バロトロピー性
- 第二項:\(\boldsymbol{K}=-\nabla U\):外力がポテンシャルエネルギー
- 第三項:粘性項は無し(非粘性流れ)
ということ条件で考えることにします。
ナビエストークス方程式(3つの条件を課す)
\frac{\partial \boldsymbol{v}}{\partial t}+\big(\boldsymbol{v}\cdot \nabla\big)\boldsymbol{v}=-\nabla P-\nabla U\tag{9}
\end{align*}
これで①の準備は完了です。
②の項について
(7)式の第二項の\(\boldsymbol{v} \cdot\frac{D d\boldsymbol{r}}{Dt}\)は、数学的には少々厳密性を欠きますが以下のように計算を進めることができます。
まず、\(d\boldsymbol{r}\)は線素の微小変化なので、
d\boldsymbol{r}=\boldsymbol{r}_{2}-\boldsymbol{r}_{2}
\end{align*}
と考えても良いでしょう。
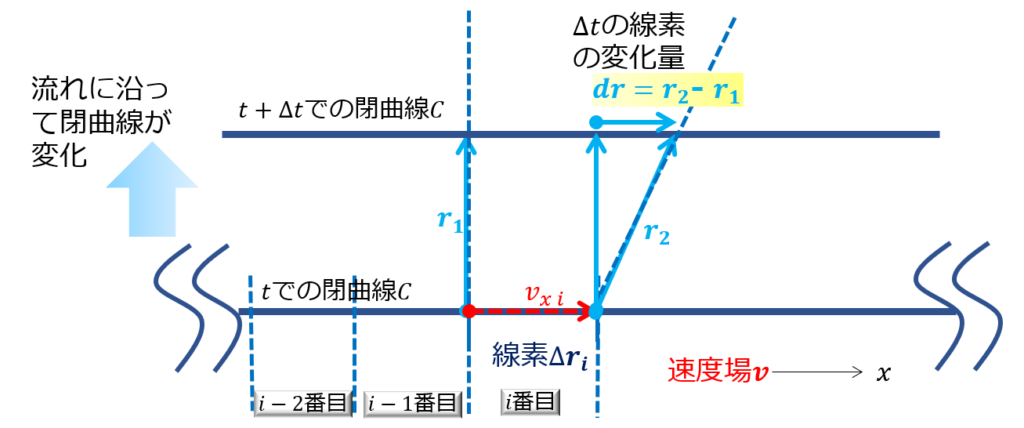

ゆえに、下記のように計算できます。
\frac{D (\boldsymbol{r}_{2}-\boldsymbol{r}_{1})}{Dt}=\frac{D (\boldsymbol{r}_{2})}{Dt}-\frac{D (\boldsymbol{r}_{1})}{Dt}=\boldsymbol{v}_{2}-\boldsymbol{v}_{1}=d\boldsymbol{v}\tag{10}
\end{align*}
このように、\(\frac{D d\boldsymbol{r}}{Dt}\)は、速度変化量\(d\boldsymbol{v}\)と書けることがわかりました。
ということで、②の部分は、
\boldsymbol{v} \cdot\frac{D d\boldsymbol{r}}{Dt}=\boldsymbol{v}\cdot d\boldsymbol{v}\tag{11}
\end{align*}
と準備完了です。
ケルビンの循環定理の証明
ここからケルビンの循環定理の証明をやっていきたいと思います。
循環の時間変化を3つの条件を課して計算してみる
さて、3つの条件をまた書いておきます。
さきほど下記の①と②の部分が整理できたので、(6)式に代入して計算を進めてみましょう。
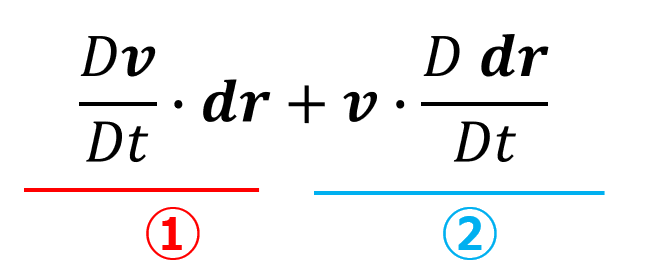
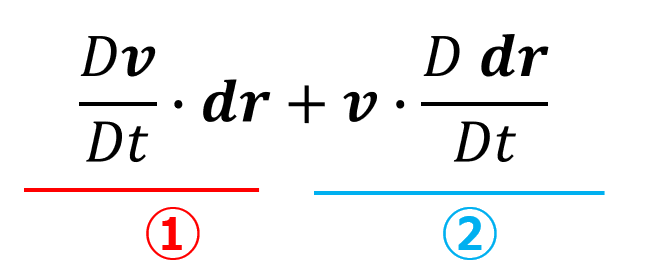
\frac{D}{Dt}\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=-\oint_{c} \bigg(\nabla P+\nabla U \bigg)\cdot d\boldsymbol{r}+\oint_{c}\boldsymbol{v}\cdot d\boldsymbol{v}\tag{12}
\end{align*}
(12)式右辺の第一項については、例えば\(U\)の積分は、
-\oint_{c} \bigg(\nabla U \bigg)\cdot d\boldsymbol{r}=-\oint\bigg(\frac{\partial U}{\partial x}dx+\frac{\partial U}{\partial y}dx+\frac{\partial U}{\partial z}dx\bigg)
d\boldsymbol{v}
\end{align*}
となって、\(U\)が1価関数なら1周線積分すると消えてしまいます。
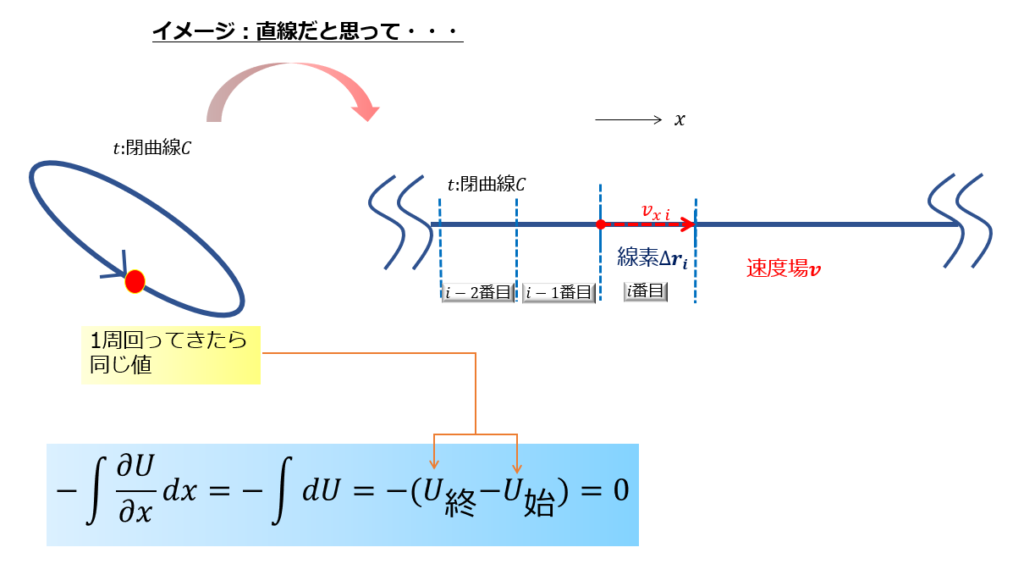

\(P\)についても同様ですよね。
さらに、(12)式右辺の第二項については、
\oint_{c}\boldsymbol{v}\cdot d\boldsymbol{v}=\oint_{c}d\bigg(\frac{1}{2}\boldsymbol{v}^2\bigg)
\end{align*}
と書き前ることができます。
だから(12)式は、
\frac{D}{Dt}\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=-\bigg[ \nabla P+\nabla U \bigg]_{c}+\bigg[\frac{1}{2}\boldsymbol{v}\bigg]_{c}=0\tag{13}
\end{align*}
となって、1周ぐるっと積分してもとの位置に戻ってきたことになりますので結局0になります。
最後にまとめで得たことをまとめておきます。
まとめ
下記の3つの条件を課すと、流れに沿って変化する循環の時間変化を考えると、循環は変化しない。




循環が変化しない(保存)
\frac{D\Gamma_{c}}{Dt}=0\tag{14}
\end{align*}
これは、良い知見を得たように思えます。
渦度はその名の通り渦を定義する一つの物量であります。
で、循環は渦度に関係する量であるということを冒頭で述べましたよね。
その循環が、下記の3つの条件を課すと、時間変化しないということをケルビンの循環定理が教えてくれます。
ということは、
循環が0・・・つまり渦度が0・・・渦がない状態から始まったら上記の条件のもとでの流れであると、ケルビンの循環定理より循環はず~っと0である、
つまり渦はどう頑張っても生成できないということを教えてくれています。
確かに上記の3つの条件を課すことは実現象ではあまりに限定され過ぎた流れでしょう。
ならば、上記のような条件を課さなければケルビンの循環定理は成り立たないということになります。
言い換えると、上記の3つの条件のうちのどれかでも崩れると、渦を生成しても良いという結論になります。
次回
次回のヘルムホルツの渦定理の内容を書きます。
- 流体力学の循環の定義
- ケルビンの循環定理←本記事の内容
- ヘルムホルツの渦定理←次回の内容
- ラグランジュの渦定理
- ケルビンの循環定理を破る例(量子流体を例にする)
渦が生成される例を紹介
渦が生成される例の紹介として下記の記事をご堪能下さい。
OpenFOAMというオープンソースのCAE解析ソフトを使って、流体解析をしてみました。
5番目の記事は、2相の間のせん断応力で渦をつくるというケルビンヘルムホルツ不安定性と呼ばれるやつです。
↓こんな感じ。


流体力学を深く理解するための参考書
初心者から中級者で流体力学を学ぶのにおすすめの参考書を以下に列挙しておきます。
流体力学は、「工学向け」か「理学向け」で内容が結構変わってきます。
工学部向け流体力学
工学向けでは以下の3冊をお勧めします。
👆こちらは、初心者でもわかりやすく理解できると思います。
演習書としては以下のものが、難しすぎず・・・がっつり練習できます。
工学部であれば圧縮性の流体まで、学ぶことが多いと思いますので、「圧縮性流体」の参考書としては以下の書籍がお勧めです。
理学部向け流体力学
僕は、理学部出身なので主に愛用していた書籍を紹介します。
👆こちらの書籍は流体力学を学ぶために一番最初に購入した本なのですが、今まで読んだ流体力学の中で一番わかりやすいと思っています。
ただ、残念過ぎるのは「前編」だけを書いて著者がお亡くなったため、「後編」がないという参考書です。それなのに絶版にならずに書籍で見かけるんですから、相当有名なんだろうなと思います。
もう少し優しい参考書としては「今井氏」の流体力学がお勧めですね。
※最後に「1000ページ」くらいの乱流力学の教科書も紹介しておきます(笑)
買ってしまった。。。https://t.co/RPaZNZ3cxv
— カマキリ🐲@物理ブログ書いている (@t_kun_kamakiri) May 16, 2020