本記事では、マイヤーの関係式についての理解をまとめておきたいと思います(^^)/
はい(^^)
とてもシンプルな関係式ですね。
この関係式の面白いところは、どんな気体なのかに関わらず、理論気体であればマイヤーの関係式が成り立つという点です。
定圧比熱と定積比熱のまとめ
下記の記事を参考に、定積比熱と定圧比熱はどのように定義したかを理解しておきましょう。
定圧比熱と定積比熱の表式についてまとめました。
| No. | 環境下 | 0の変化量 | 比熱の色々な表記 |
| A | 圧力も体積も変化 | – | – |
| B | 体積一定 | \(dv=0\) | \(C_{V}\):定積比熱 \(C_{V}\):定積比熱の単位は、\((J/mol \,K)\)
体積一定下において、1mol当たり、1K(もしくは1℃)上昇させるのに必要な熱量(J) |
| C | 圧力一定 | \(dp=0\) | \(C_{p}\):定圧比熱 \(C_{p}\):定圧比熱の単位は、\((J/mol \,K)\)
圧力一定下において、1mol当たり、1K(もしくは1℃)上昇させるのに必要な熱量(J) |
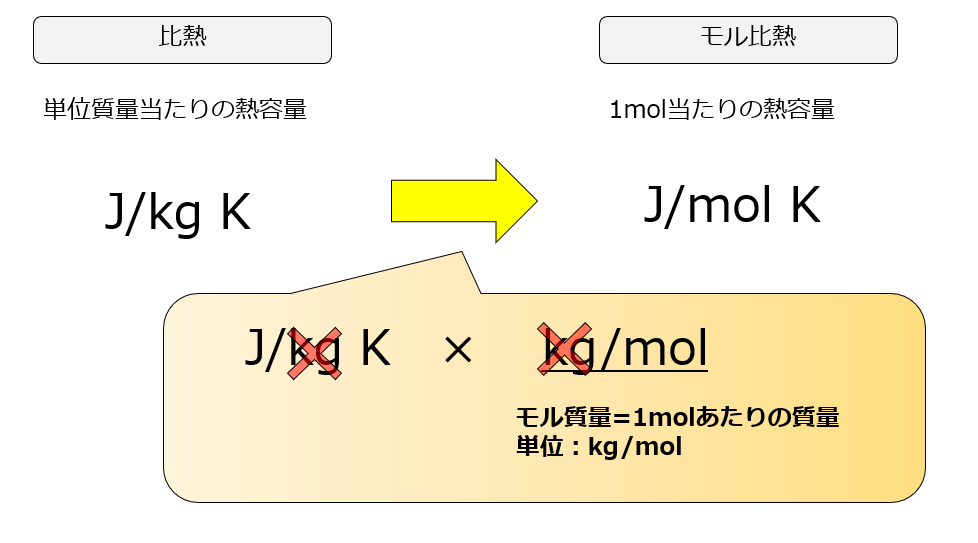
比熱の単位が1mol当たり1℃上昇するのに必要なエネルギー[J/mol K]で定義しているのか、単位質量当たり1℃上昇するのに必要なエネルギー[J/kg K]で定義しているのか、分野によって向き不向きがあるので、参考書を読む際は単位には十分に注意しましょう。
マイヤーの関係式の導出
マイヤーの関係式は以下の流れで導出できます。
- 熱力学第一法則を立式
- 定圧比熱と定積比熱の関係式を導出
- 理想気体の状態方程式を導入
マイヤーの関係式は大学院入試問題でも出てくる有名な関係式です。
熱力学第一法則を立式
これらは熱力学第一法則、
※外部へする仕事量は\(d^{\prime}W\)、気体の圧力\(p\)がする仕事のみを考えて\(d^{\prime}W=pdV\)と書きます。
※\(d^{\prime}Q=dU+d^{\prime}W\)は教科書では「状態量」と「状態量でないもの」を区別するために「’(プライム)」をつけて区別する場合があります。
「’(プライム)を付けたものは」状態量ではないということを明記することがあります。
内部エネルギー\(U(T,V)\)は独立な変数として、温度\(T\)、体積\(V\)を指定します。
ここで、内部エネルギー\(dU\)の全微分を考えると、
と書けるので、(1)式に代入して、
d^{\prime}Q=\bigg(\frac{\partial U}{\partial T}\bigg)_{V}dT+\bigg(\bigg(\frac{\partial U}{\partial V}\bigg)_{T}+p\bigg)dV\tag{3}
\end{align*}
を得ることができます。
定圧比熱と定積比熱の関係式を導出
(3)が意味することは、左辺\(d^{\prime}Q\)のように加えられたエネルギー(熱量)である$Q$は変数\(T\),\(V\)として変化する量となります。
※熱力学にはいっぱい変数が出てきますが、粒子数が一定の場合独立な変数は実は2つだけです。
定圧比熱\(C_{p}\)を用いて書くためには、(3)の熱力学第一法則で圧力$p$固定した状態で温度で微分すれば良いです。
つまり、定圧比熱の定義から$nC_{p}=\big(\frac{\partial Q^{\prime}}{\partial T}\big)_{p}$が言えます。
nC_{p}=\bigg(\frac{\partial U}{\partial T}\bigg)_{V}+\bigg(\bigg(\frac{\partial U}{\partial V}\bigg)_{T}+p\bigg)\bigg(\frac{\partial V}{\partial T}\bigg)_{P}\tag{4}
\end{align*}
\(\big(\frac{\partial U}{\partial T}\big)_{V}=nC_{v}=C_{v}\)(1モルで考えるなら)
と置くことができて、定積比熱\(C_{v}\)と書けるます(^^)/
定積比熱の定義
(4)の第1項に定積比熱の定義式を代入します。
\end{align*}
ここまでで、定圧比熱と定積比熱の関係式が完成しました(^^)/
(6)はマイヤーの関係式とは言わず、あくまで熱力学第一法則を式変形することで得られた定圧比熱と定積比熱の関係式です。
理想気体の状態方程式を導入
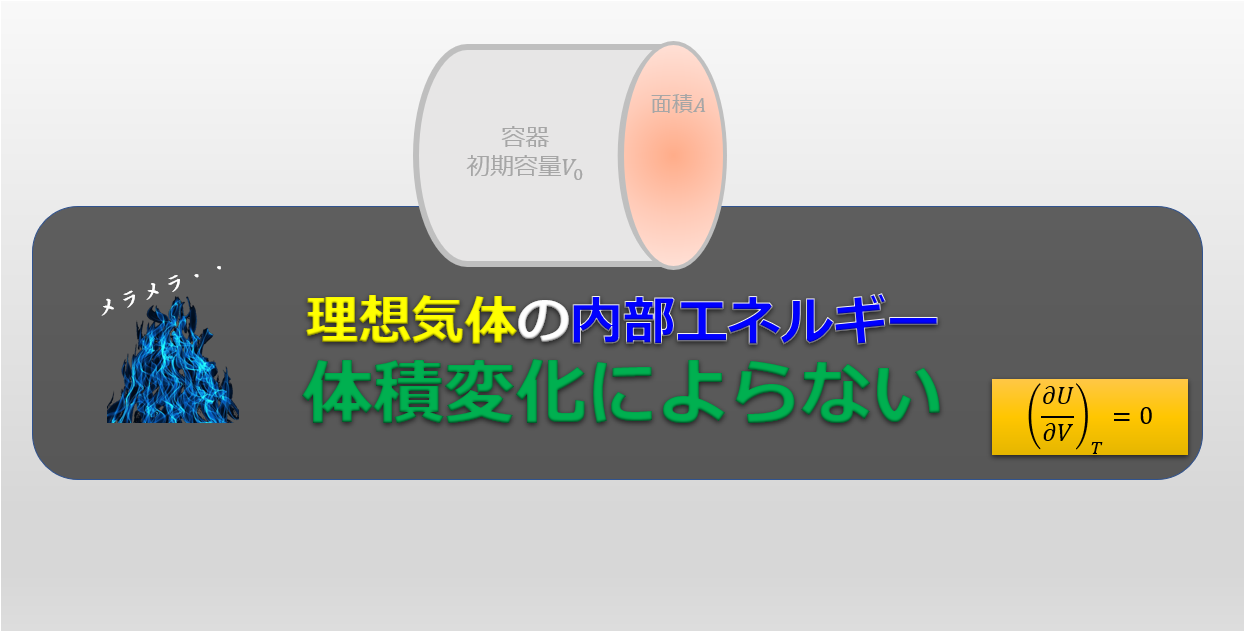
さらに、(6)の第二項の\((\frac{\partial U}{\partial V})_{T}\)は、理想気体を考えている場合は0になることがことが知られています。
理想気体の場合は内部エネルギー$U$は温度$T$のみの関数なのです。
なので、理想気体の条件下では(6)式は下記のようにとても簡単に書くことができます。
\end{align*}
ここで・・・
理想気体の状態方程式
を使うと、(7)式は・・・
\end{align*}
⇔
C_{p}=C_{v}+R\tag{8}
\end{align*}
と書ける。
この(8)式が「マイヤーの関係式」と呼ばれています関係式です。
まとめ
本記事では、以下3つの手順によりマイヤーの関係式を導出しました。
- 熱力学第一法則を立式
- 定圧比熱と定積比熱の関係式を導出
- 理想気体の状態方程式を導入
マイヤーの関係式は理想気体であれば、気体の種類に依らず(分子の構造の詳細に依らず)成り立つ関係式です。
理想気体が成立する仮定とは・・・
- 分子の大きさが無視できる⇔希薄気体
- 分子間力相互作用が無視できる⇔高温状態
また理想気体であれば、内部エネルギーが体積\(V\)には依存せず温度のみに依存することを覚えておきましょう(^^)/
※マイヤーの関係式は、どんな温度状態でも成立するものであるとは限りません。
例えば、ここで議論している内部エネルギーは統計力学などの分子の詳細モデルで語るのであれば「分子の並進運動エネルギー、分子の回転運動エネルギー」が主なエネルギーでありますが、その他にも分子の励起振動エネルギーなども本来はモデル化されている必要があります・・・・・・
が、熱力学の範疇でそのようなエネルギーは考慮していません。
ですので、高温状態になった際に励起振動エネルギーが目立ってくると、マイヤーの関係式も実現象から乖離してくる理論式となってしまいます。
やはり、常にどのうな条件で成り立っている理論式なのかを理解しておく必要があります(‘ω’)
最後に注意(単位には気を付けて)
マイヤーの関係式は
C_{p}=C_{v}+R\tag{8}
\end{align*}
このように書けるのですが、単位には注意が必要です。
本記事では比熱はモル比熱[J/mol K](1molの気体を1K上昇させるのに必要なエネルギー)として定義して式変形を行いましたが、分野によってはモル比熱[J/kg K](1kgの質量の気体を1K上昇させるのに必要なエネルギー)として式を書いている場合があります。
モル(mol)で考えているか質量で考えているかの違いです。
たとえ質量で考えてもマイヤーの関係式は、同じように$C_{p}=C_{v}+R$と書かれることがありますが、このときの単位に注が必要です。
定圧比熱は$C_{p}$[J/kg K]、定積比熱は$C_{v}$[J/kg K]となっている場合は、気体定数である$R$の単位も[J/kg K]となっています。
気体定数はだいたい8.314[J/mol K]くらいと気体に依らず決まった値を取っているのですが、これはあくまでmolで考えた場合です。
1kgあたりで考えた場合は、この気体定数が気体の種類ごとの気体定数となります。
式で書くと$\frac{R}{M}$のことです。
- 気体定数$R=8.314$[J/mol K]
- 分子量$M$[kg/mol]
※分子量とは「1molあたりの質量[kg]」です。
だから、molで考えるか1kgあたりで考えているかで同じだと思っていた気体定数の値が違ってくるということを覚えておく必要があります。そうでないと、参考書によってはmolかkgのどちらをベースに書かれているかによって、値が変わってくるのでとても混乱することになります。
なので、僕は以下のようにあえて区別して書くようにしています。
これを両辺、気体の分子量$M$[kg/mol]で割ると、
記号表記はお任せします。
とにかくmolで扱っているか、kgで扱っているか、単位が違うと値が異なるので参考書を読むときは注意をしてください_(._.)_
参考文献
熱力学を勉強するにあたってとても参考になる参考書を紹介しておきます(^^)/
以上の2冊(田崎さん、清水さん)の参考書はとても勉強になります。
内容は結構ハードですが、じっくり読めばとても理解が深まる良書です。
もう少し優しい内容で勉強したい場合は以下2冊がおすすめです。