こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
理想気体における内部エネルギーについてとても重要な事実を示しておこうと思います。
次の事実です。
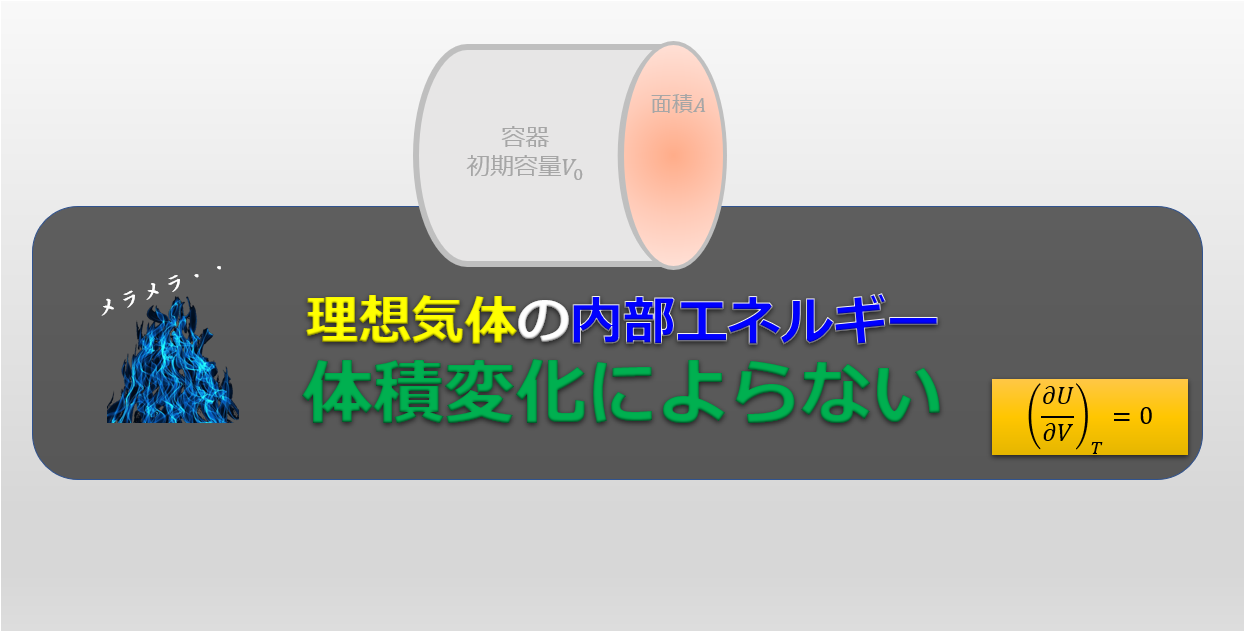
理想気体の内部エネルギーは温度にのみ依存し、
体積には依存しない!覚えておこう!
これは覚えてしまいましょう!!
これは熱力学の参考書で超有名な「田崎 熱力学」にも書いてあることですが、
といったことも書かれているくらいです。
※完全なる引用ではないので、一度ちゃんと読んでみてください。
熱力学第一法則から考える
今から何を考えたいかを先に示しておきましょう。
理想気体の場合・・・
温度変化しない場合に容量が変化すると内部エネルギーはどう変化するのか?
つまり・・・・
\bigg(\frac{\partial U}{\partial V}\bigg)_{T}
\end{align*}
↑これを考えたいと思います。
では、熱力学の要請であるマクロな系でのエネルギー保存則「熱力学第一法則」から考えることにしましょう。
熱力学第一法則
※\(d^{‘}\)とついているものは状態量ではありませんよという印みたいなものだと思ってください。
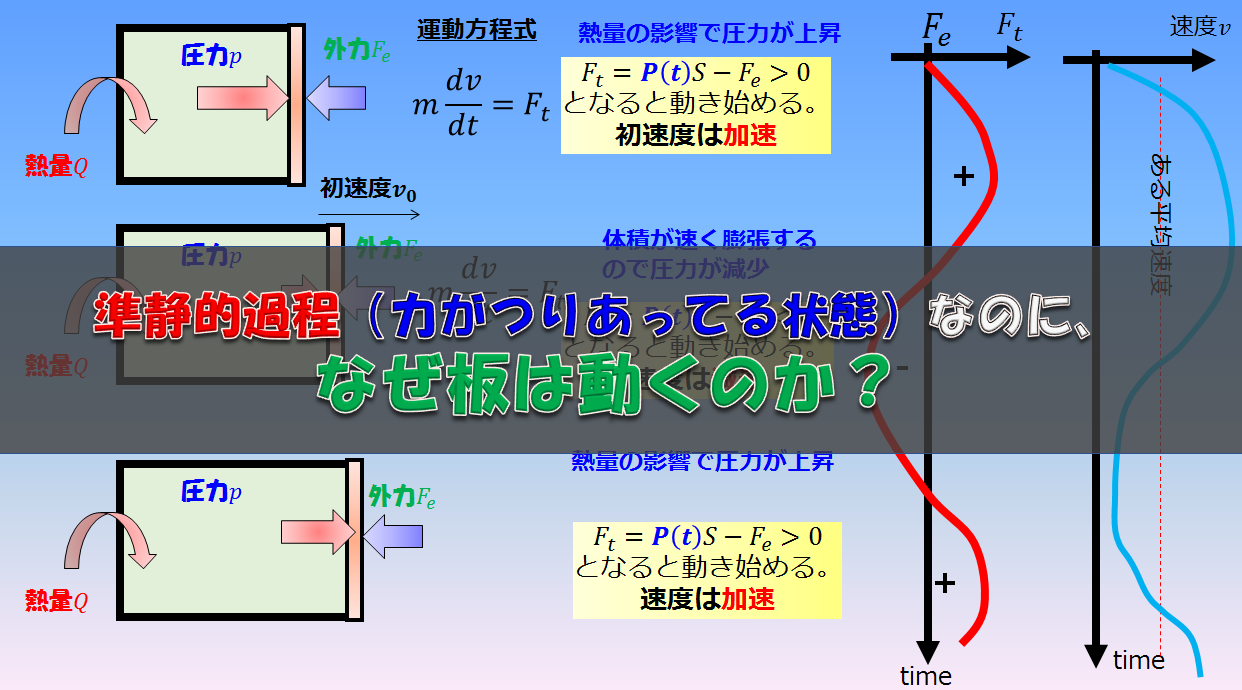
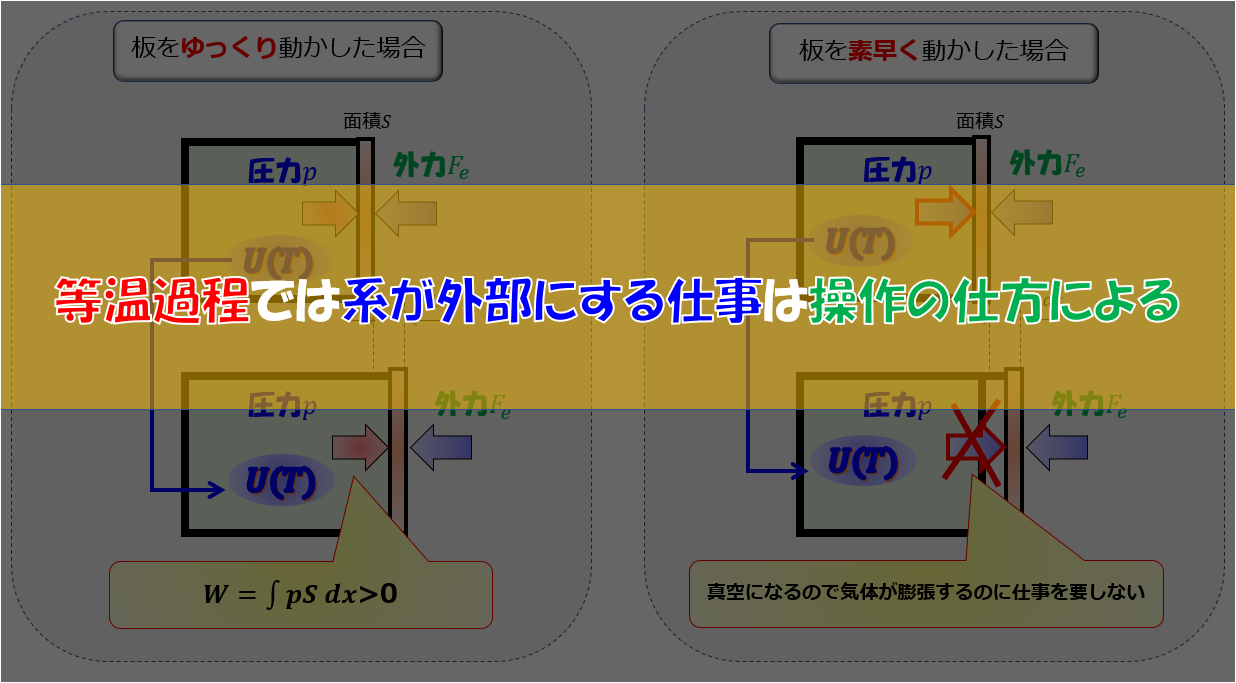
\(dW\)に対しては気体が外にする仕事を意味していますが、今回の場合は気体が外にする仕事は外気圧\(p_{ex}\)と釣り合っている状態(準静的過程)で膨張することになるので、
が成り立ちます。
なので(1)式は、
と書いてしまいます。
(2)式に対して、\(T\)を固定して\(V\)で偏微分することを考えましょう(^^)/
ここで、エントロピー\(S\)を導入します。
\(d^{‘}Q=TdS\)なので、(2)式は、
となりますね。
お!!目的の式が右辺に出てきました!!
左辺のエントロピーとかいう謎の物理量が邪魔なのですが、これはマクスウェルの関係式を使って圧力\(p\)や温度\(T\)など馴染みのある物理量に変換しておきます。
マクスウェルの関係式のうち、今回使うのは、
これを(3)式の左辺に適用すると、
⇔
(6)式は重要なので覚えておきましょう(^^)/
ここまでは余計は仮定を使っていないので一般論をただ述べていっただけです。
では、理想気体だとどうなるのでしょうか?
理想気体の内部エネルギーは体積\(V\)によらない
ここからが理想気体の場合はどうなのかというのを考える章です。
理想気体の状態方程式
を用いると、(6)式がどうなるか計算してみましょう。
めんどうなのは、\(\big(\frac{\partial P}{\partial T}\big)_{V}\)くらいですかね。
計算すると\(\frac{nR}{V}\)となります。
結局、(6)式の右辺は0になります。
つまり・・・・
が証明できたことになります(^^)/
まとめ
理想気体の場合は、内部エネルギーが体積\(V\)に依存しないことが示せました(^^)/
めっちゃ重要な補足:理想気体の内部エネルギーは体積\(V\)変化させても絶対変化しないのか?
注意が必要なので、補足しておこうと思います。
本記事の内容を読んで、理想気体の場合は内部エネルギーが体積\(V\)に依存しないということがわかったと思います。
では、
(問い):体積変化させる場合に何をやっても内部エネルギーは変わらないのでしょうか?
僕はしばし考えました・・・・・
(答え):そういうことではないですよね。
そこを注意しておかないと誤解が生じます(‘ω’)
なぜかと言いますと、熱力学の状態というものは2つのマクロな物理量(例えば、圧力や温度・・・など)を決めることでその他の物理量が決定されるのですが、体積だけ決めたからと言って内部エネルギーが決まるわけではないです。
今回の場合は、内部エネルギーが何に依存しているのかをわかりやすくするために温度を固定しました・・・・
すると内部エネルギーを決定する要素として体積のみになり、結果は内部エネルギーが体積に依存しないということがわかったということです。
しかし、「体積が変化する→圧力が変化する(ついでに温度も変化している)→結果、内部エネルギーが変化している」というケースはあります。
例えば、断熱過程において、外から力を加えると体積が減少⇒結果、圧力が上昇します。
このとき、すでに熱力学状態変数のうち2つが決定しているため、温度も決定することができます。
断熱過程においては、以下のポアソンの公式というのが使えますね。
- \(pV^{\gamma}=const\)
- \(TV^{\gamma-1}=const\)
これより、体積が減少しているのであれば、温度が上昇していることがわかります。
ゆえに、内部エネルギーが上昇しているという結果になります。
つまり、重要なことは理想気体の内部エネルギーが温度のみに依存しているということだということに気付くことでしょう!
ここで、
「理想気体を考えている条件下では、内部エネルギー$U(T,V)$は$V$に依存しないのか。。。(‘_’)
ならば、$\frac{dU}{dV}=0$なのかな??」
というのを考えたいと思います。
良く見てほしいのですが、温度$T$が一定下であれば(7)式が成立するということしか言っていません。
本来は$\frac{dU}{dV}$と$\frac{\partial U}{\partial V}$とは意味が違うのです。
↓全微分と偏微分の違いはこちらを参考にしてください。
熱力学状態変数を仮に\(V,T\)とした場合は以下のようになります。
\tag{8}\end{align*}
⇔
\end{align*}
(7)式によって、第一項は消えます。
\frac{dU}{dV}=\bigg(\frac{\partial U}{\partial T}\bigg)_{V}\frac{dT}{dV}\tag{10}
\end{align*}
このようにして、「$\frac{dU}{dV}$自体は0ではなさそう」であることがわかりました。
(10)式からは、理想気体であっても「体積変化をして温度が変わるのであれば、内部エネルギーは変化するよ」ということを意味しており・・・・
内部エネルギーは体積変化に対して変化しないんだけど、温度が変わると内部エネルギーは変わるよ・・・・体積変化したことが直接的な原因じゃないからね・・・ってなんか遠回しに語りかけています(笑)
熱力学状態変数を仮に\(V,p\)とした場合は以下のようになります。
\frac{dU}{dV}&=\bigg(\frac{\partial U}{\partial p}\bigg)_{V}\frac{dp}{dV}+\bigg(\frac{\partial U}{\partial V}\bigg)_{p}\frac{dV}{dV}\\
&=\bigg(\frac{\partial U}{\partial p}\bigg)_{V}\frac{dp}{dV}++\bigg(\frac{\partial U}{\partial V}\bigg)_{p}\tag{10}
\end{align*}
何を熱力学状態変数にするかによって、$\frac{dU}{dV}$も色々な形になりますね。
理想気体の場合は、内部エネルギーは$\frac{dU}{dV}=0$というわけではなく、$\big(\frac{\partial U}{\partial T}\big)_{V}=0$であるということを意識して覚えましょう。
- $\frac{dU}{dV}=0$⇒×
- $\big(\frac{\partial U}{\partial T}\big)_{V}=0$⇒○
お勧めの「熱力学」の参考書
数多くある熱力学の参考書の中から、厳選してこの4冊はお勧めできるよっていうのを、ピックアップして紹介しています。