気体が膨張すると温度は下がるのか。それとも温度は上がるのか。

こんにちは（@t_kun_kamakiri）(‘◇’)ゞ

容器にnモルの気体を入れて出入りできなくします。
その状態で容器の容量を増やします。
平衡状態になるまでしばらく待ちます。
どうなると直感的に思いますか？
※理想気体と仮定

状況設定をあまり伝えず・・
直感的にはどう思うものなのかな？(・o・)

— カマキリ🐲@物理ブログ(宇宙に入ったカマキリ) (@t_kun_kamakiri) 2019年5月30日

面白い結果になりました。

「温度が下がると思う人」と「内部エネルギーを考えてから判断する」といった2つの意見にわれました。

面白いアンケート結果だと思います(^^)/

このような質問をされたときに、僕は感覚的には、温度が下がると回答しそうですが・・・・よくよく考えると、もう少し詳細な状況設定を考えないと何とも言えないというのが正確な回答ではないかと思います。

熱力学第一法則を考えて内部状態（内部エネルギー）がどうなっているかを考えないと判断できないというのが正解ではないかと思っています。

では・・・

これらの考察をしたいと思います(^^)/

なぜ温度が下がると回答した人が多かったか？

正確な状況設定を伝えていないから、気体が膨張すると温度が下がるというのは感覚的には正しいと思っています。

「温度が下がると回答した人」の多くの人は、気体の断熱膨張を想像したからですね。

• 断熱的な系：外部との熱のやりとりをしない系
• 膨張：気体が体積を増やす

日常で起こるような気体の膨張過程では、気体が膨張するときに熱を放出したり、熱が入ってくるという状況をあまり想像しないから、

単に気体が膨張するとどうなるかと聞かれると断熱膨張過程を感覚的に思い浮かべてしまうのも無理はないかと思います。

では、断熱膨張を熱力学第一法則から考えてみましょう。

熱力学第一法則

\(d^{‘}Q\)：正味の熱量
\(dU\)：内部エネルギー変化
\(d^{‘}W\)：気体が外部へする仕事

ここから断熱過程\(d^{‘}Q=0\)を考えると、

ここから気体を膨張させることを考えるのですが、容器に閉じ込めていた気体を大気中に解き放っても良いですし、無理やり板を動かして気体を膨張させても良いです。

いずれにしても、気体が膨張するときに外へ仕事をすることになるので、\(d^{‘}W>0\)となります。
よって、
内部エネルギー変化\(dU<0\)ということになります。

つまり、断熱膨張だと気体の内部エネルギーは減っているということです。

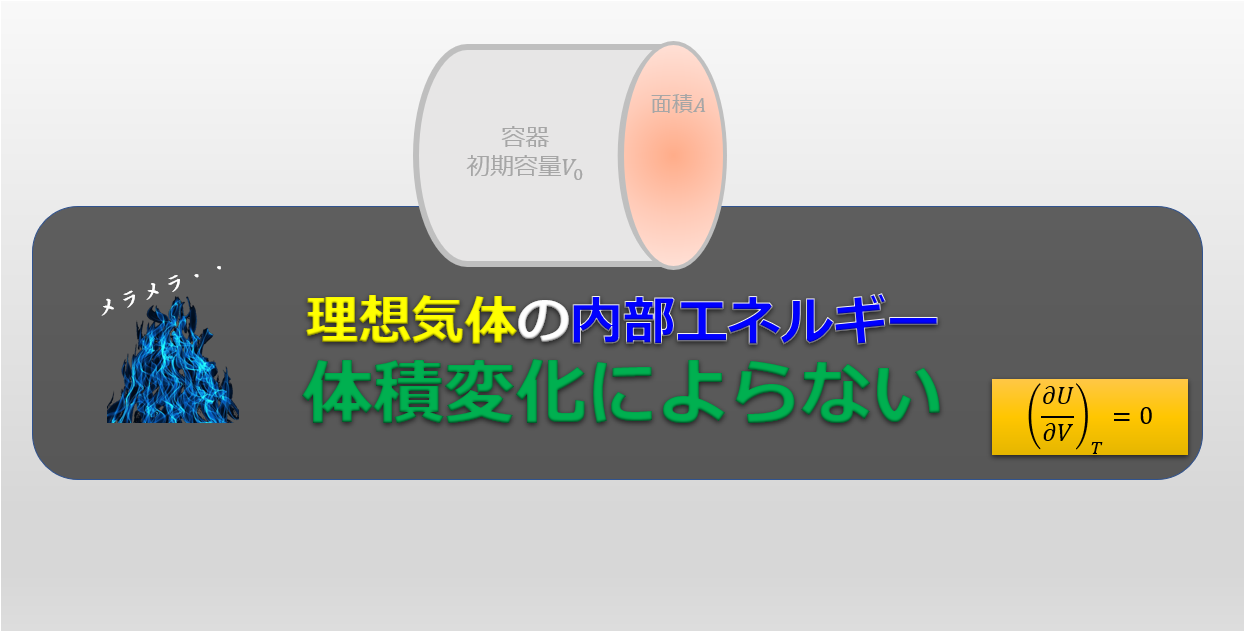
ここで・・・理想気体の内部エネルギーはどのように書けるのだったか？

理想気体の場合は、内部エネルギーは温度の増加関数ということです。
↑超重要なので覚えておきましょう(^^)/

ということで、内部エネルギーが減っているのであれば、温度が下がっているという結論になります(^^)/

温度が下がるという理屈には、「単に気体が膨張したため温度が下がる」というのではなく、外部に広がるのに仕事が必要で、その仕事の分内部エネルギーが下がってしまい、温度が下がるという結果になったということです。

↑いつもこのような状況とは限らないので、圧力が減ったのかというよりも「熱力学第一法則」から内部状態（内部エネルギー）がどうなったのかを考える方が良いと思われます。

理想気体なら内部エネルギーが温度のみの関数になっているのですが、下記のように実在気体だった場合はもっと複雑な状況になることでしょう。

• 内部エネルギーが体積に依存する
• 内部エネルギー以外に分子間相互作用を考慮する
• 重力を考慮する
• 分子の振動も考慮する

※内部エネルギーといえば、気体分子運動論を思い出す人も多いでしょう。
しかし、気体分子運動論は理想気体に対しての理論だということを忘れてはいけません(/・ω・)/

気体の膨張によって温度が上がる状況もあるのではないか？

「気体が膨張すると温度はどうなるか？」というざっくりとした質問では温度がどうなるかは何とも言えないのです。

温度が上がる状況を考えるのはとっても簡単です。

めちゃくちゃ有名な・・・・シャルルの法則を例に持ち出してみます。

これを見ると明らかに体積の増加に対して温度が増加しています。

ってなるの人も多いことでしょう。

あ、条件をひとつ言うのを忘れていました。

シャルルの法則は圧力一定という条件付きです。これを見落としたらいけません(/・ω・)/

初期状態で圧力はもちろん外気の圧力と釣り合っているので、そのままでは膨張することができません。

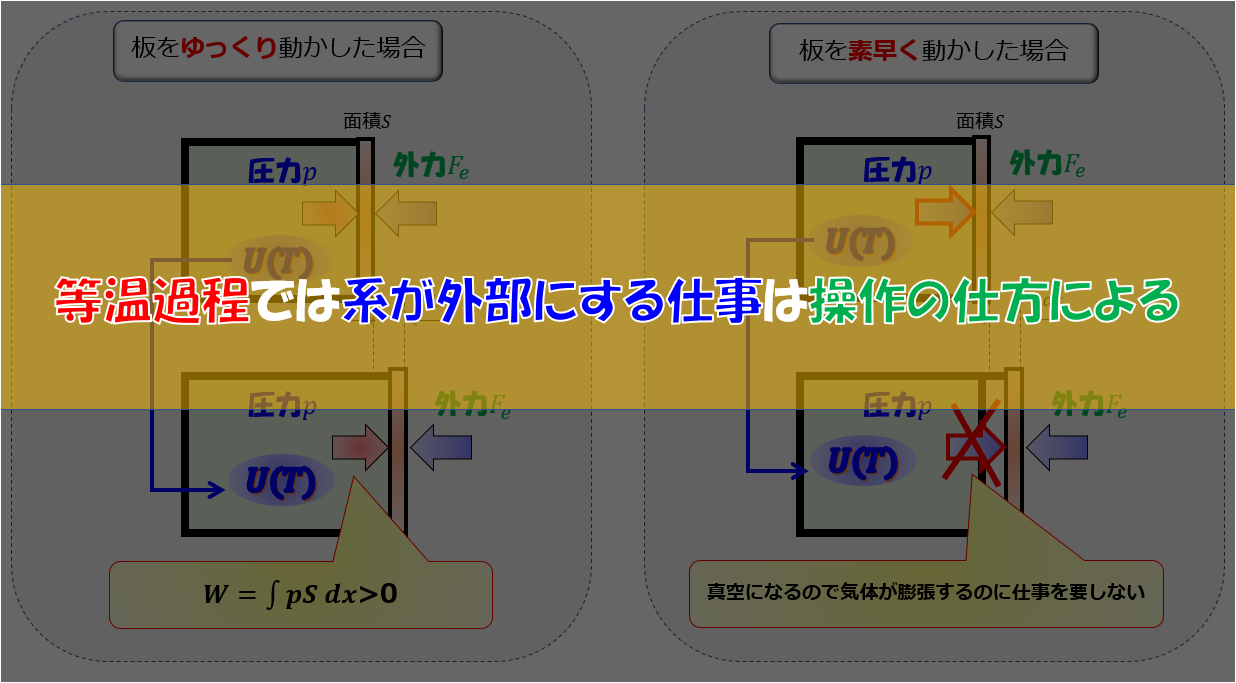
ですので、例えば以下のような方法で圧力を保ちつつ気体を膨張させるということを施す必要があります。

• 板を無理やり動かす→圧力が下がるので熱量を加える必要がある
• 熱量を加えて膨張させる→外気圧と釣り合ったまま板が動く

いずれにしても、熱量を加えていることになります。

この状況をグラフと絵で表現すると・・・

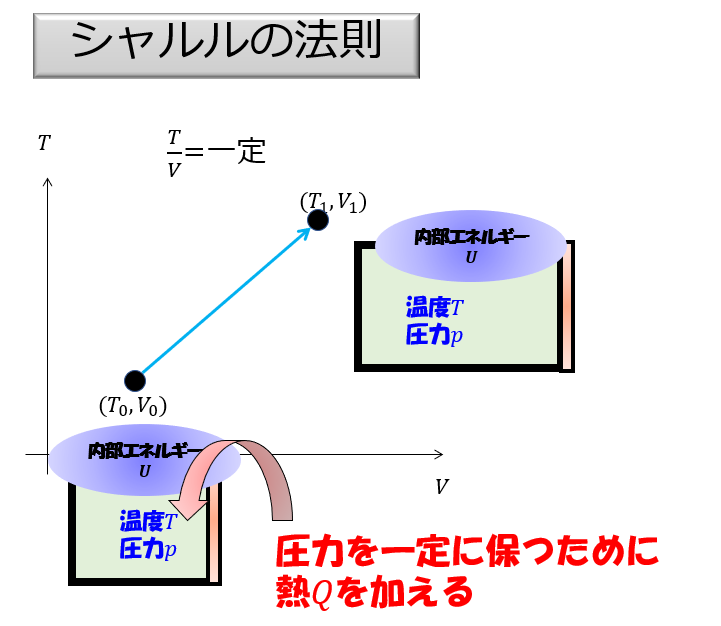
熱を加えている時点で温度上がってそうですよね。

理想気体の状態方程式\(pV=nRT\)から考えることも可能です。

理想気体の状態方程式

を内部エネルギー\(U=nC_{v}T\)を用いて式変形すると、

となります。

体積\(V\)が膨張すると圧力一定に保つためには内部エネルギー\(U\)を増加させないといけないということがわかります。

つまり、理想気体の場合は内部エネルギーが温度の増加関数なので温度が上がるというわけですね。

気体の膨張によって温度が変わらないという状況設定もできるのか？

等温過程にすればいいじゃないかという簡単な例では面白くないので、ここでは・・・

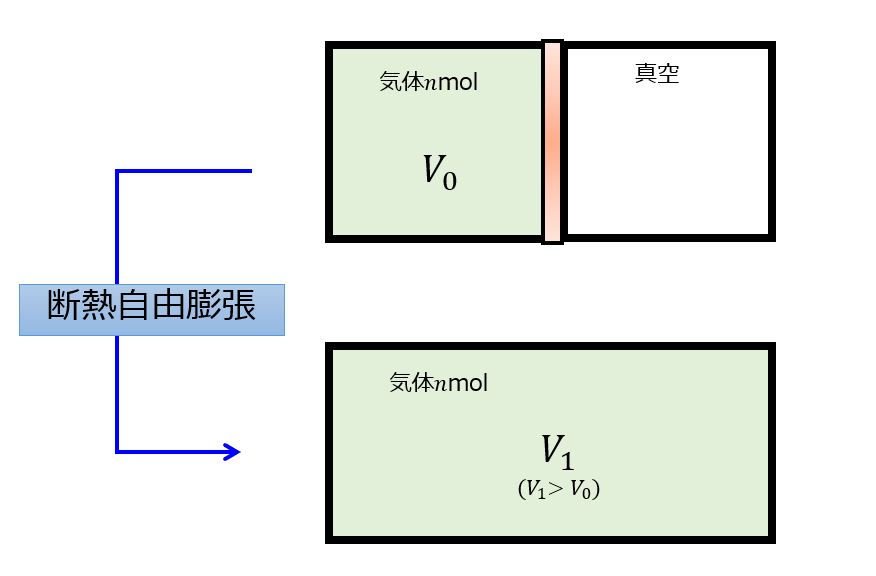
ゲーリュサックの実験というのを紹介します。

状況設定は以下です。

結果は・・・温度は変わりません。

何が起こっているのかを熱力学第一法則から真面目に考えてみましょう。

熱力学第一法則

\(d^{‘}Q\)：正味の熱量
\(dU\)：内部エネルギー変化
\(d^{‘}W\)：気体が外部へする仕事

ここから断熱過程\(d^{‘}Q=0\)を考えると、

ここまでは良いでしょう。

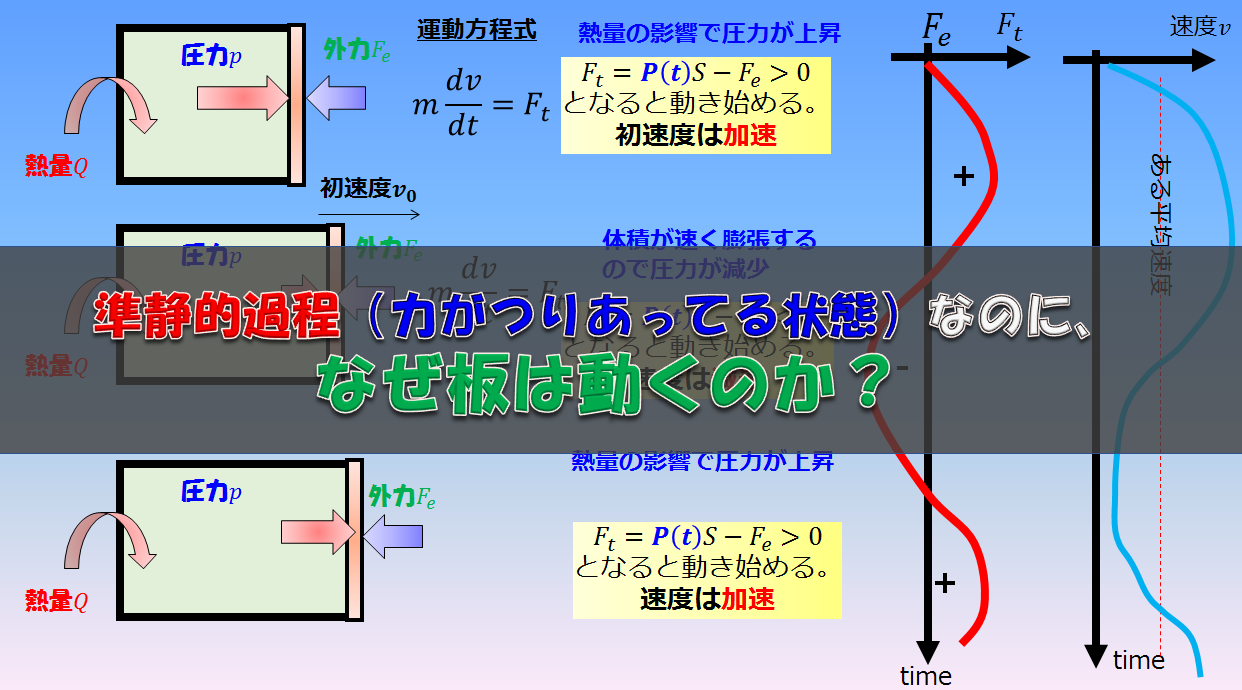
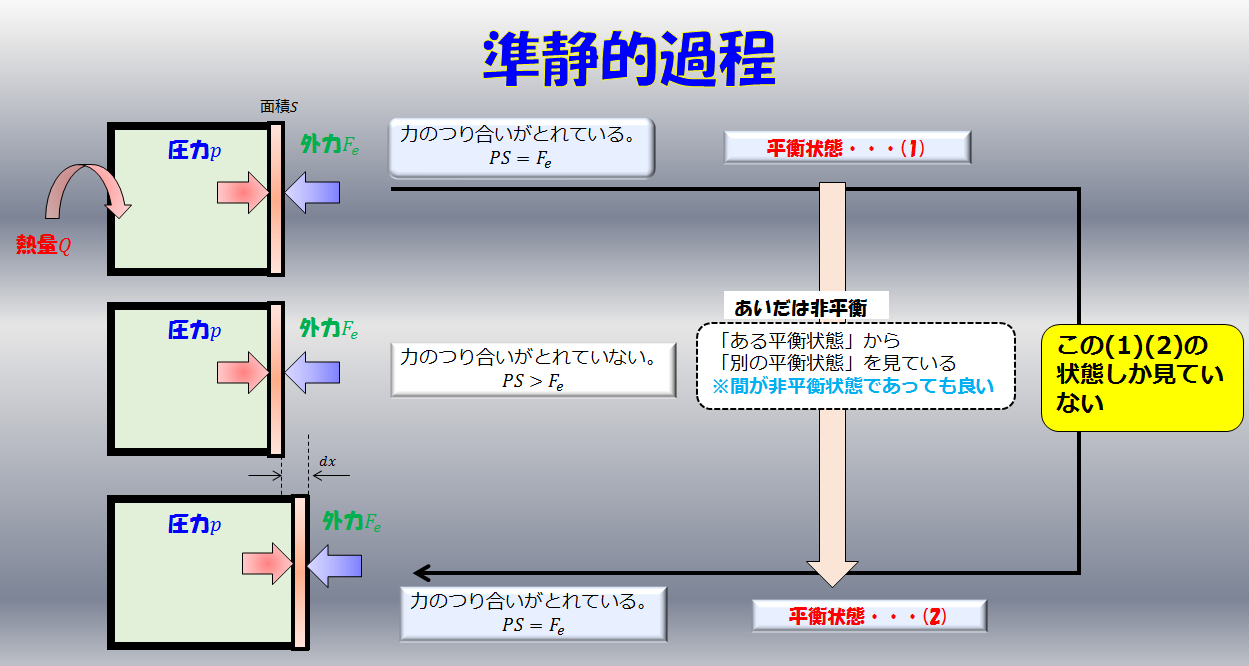
左側の気体が膨張するときに、外部とつり合いが取れた状態で膨張します（準静的過程）。
ということは、

• 左辺\(p\)：気体の圧力
• 右辺\(p_{ex}\)：外部の圧力といっても真空なので\(p_{ex}=0\)

よって、

右側の部屋が真空だったので、気体が膨張するのに全くもって仕事を必要としなかった\(d^{‘}W=0\)ということになります。

ということは、内部エネルギー\(dU=0\)ということになります。
そして、理想気体の場合は内部エネルギーが温度の増加関数であるため、

内部エネルギー変化がないのであれば温度も変化していないという結論になります。

---

ちょっとだけ注意・・・

気体が膨張するときに右側に動くための運動エネルギーはどうなったのか？
というのが疑問になります。

気体が膨張するときにはどうやらわずかに温度が下がっているそうです。
熱力学第一法則はマクロな状態のエネルギー保存則を記述するもので、エネルギーを漏れなく考えるのであれば運動エネルギーや位置エネルギーを考えないといけません。

位置エネルギーは今は考えないとして、気体が膨張するのに運動エネルギーが必要であるので、少し内部エネルギーから運動エネルギーを作って膨張すると考えられます。

ゆえに、内部エネルギーが少し下がるので温度が少し下がるということになります。

しかし、最終状態は気体の膨張も止まっているので熱平衡状態になるまで待っていると、気体の移動に使った運動エネルギーも内部エネルギーとなるため、結局温度は元に戻るということになります。

---

まとめ

今回は、「気体が膨張すると温度は下がるのか。それとも温度は上がるのか。」に対して考察を行いました。

結論は内部エネルギー状態によるということです。
それに、体積膨張をしても温度が上昇する状態も作れるのではないかと最近考えています。

断熱真空膨張の場合外部への仕事を0とみなして内部エネルギーが変わらない。理想気体を仮定すると内部エネルギーは温度のみに依存するため膨張後も温度は変わらない（ゲイリュサック・ジュールの実験）
位置エネルギーがある場合は、内部エネルギーが上昇して理想気体を仮定する気体の温度は上がる？ pic.twitter.com/ksTW2zBvdC

— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) April 25, 2021

温度が変わっているかどうかは熱力学第一法則から内部エネルギーを考えると良いです。

気体の膨張過程を考える際には、以下の点を押さえておくと良いですね。

そして、頭の中は常に以下のようなシナリオを描いておく方が良さそうです(^^)

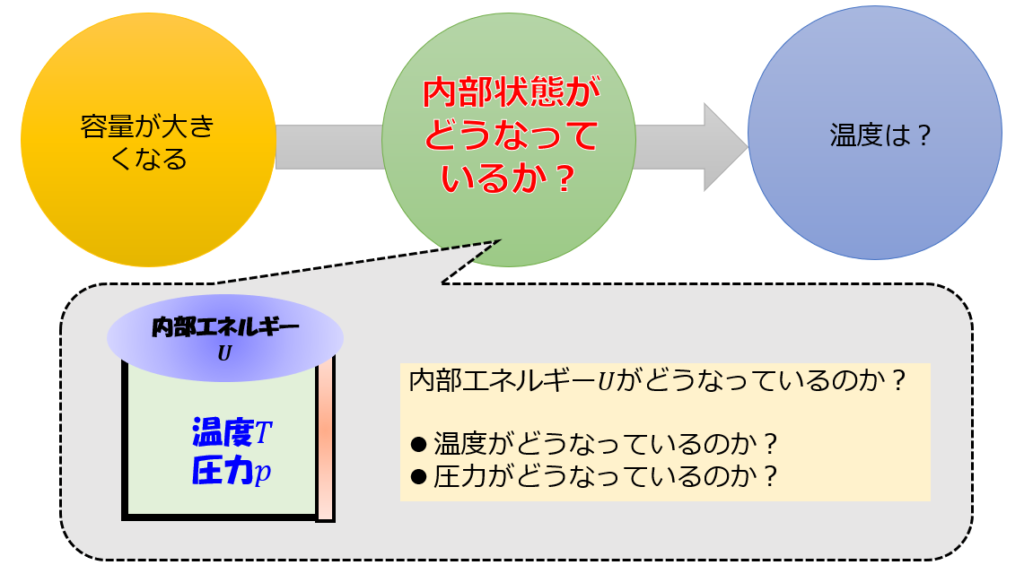
おすすめの参考書

最後におすすめの熱力学の参考書を紹介しておきます。

以上の2冊（田崎さん、清水さん）の参考書はとても勉強になります。

内容は結構ハードですが、じっくり読めばとても理解が深まる良書です。

もう少し優しい内容で勉強したい場合は以下2冊がおすすめです。