こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本記事では、熱力学で超有名な「カルノーサイクル」についてお話します。
カルノーサイクルからはじまって、
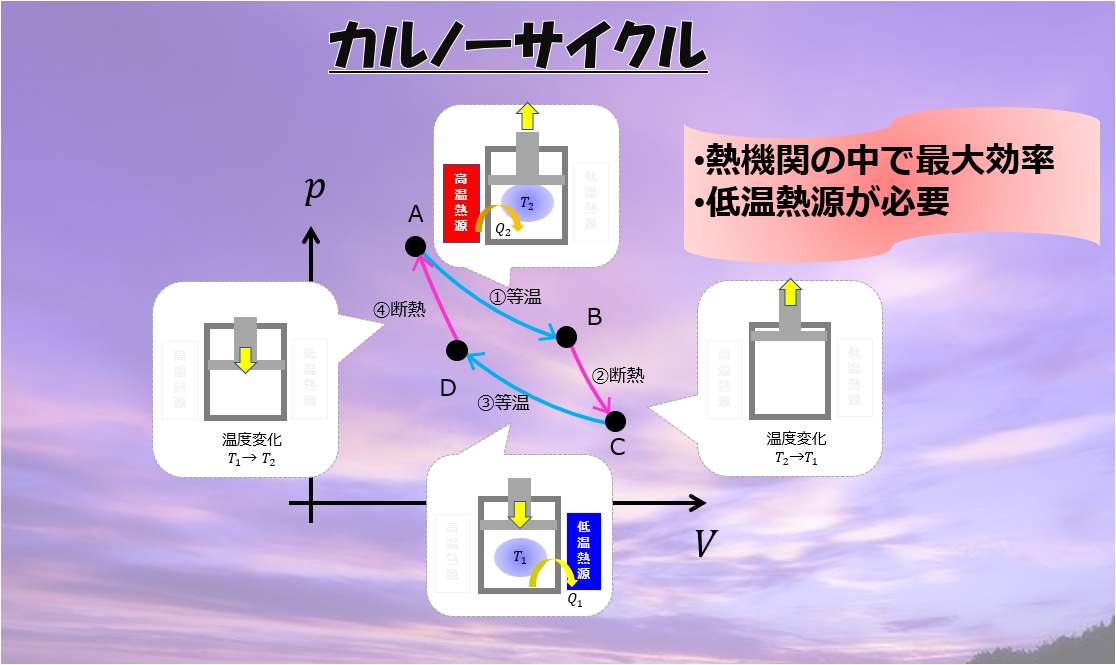
- カルノーサイクルが熱機関の中で最も効率の良いエンジンである
- カルノーサイクルには低温熱源が必要
を解説します。
さらにカルノーサイクルから、
- 熱力学第二法則(第二種永久機関は存在しない)
熱を完全に仕事に変換できるサイクルは存在しない - エントロピーとは何か?
という話にまで発展させて追々記事を書いていきたいと思います(^^)/
カルノーサイクルのカルノーって誰なの?
まず、カルノーサイクルという名前の「カルノーさん」が誰かって話をします。


こんな感じの顔です。フランスの物理学者です。
カルノーは、「熱をいかにして仕事に変えるか?」という目的の中で「エンジンの効率を上げる」ことを目的に熱力学に興味を持っていました。
熱力学は、量子力学はおろか物質の構成要素が原子からなるというよりも前に発展した学問です。
「熱の正体は何か?」という恐ろしく難しいテーマであり大昔から熱の正体について様々な提案がされています。
(有名なものとしては、「熱素」とかいうものが熱の正体だとか・・・)。
それはさておき・・・・・
熱力学は、18世紀の工業社会において「熱をいかにして仕事に変えるか?」という目的で大きく発展しました。
ゆえに、熱と仕事は切っても切れない関係です。
カルノーサイクルは「熱を仕事に変える最大効率のエンジンサイクル」です
ここで・・・・
最大効率のエンジンとはどういうことでしょうか?
「最大効率」という意味を理解するために、適当な役に立たないサイクルを考えてみましょう(^^)/
役に立たないサイクルとは?
カルノーサイクルがいかに効率が良いかを考えてるために、効率が悪い役に立たないサイクルとはどういうことかを考えてみましょう。
例えば、下記のように熱量を加えて外部に仕事をする熱機関を考えます。
(ステップ1)わかりやすくするために、温度は一定になるような過程を考えます(等温膨張)。
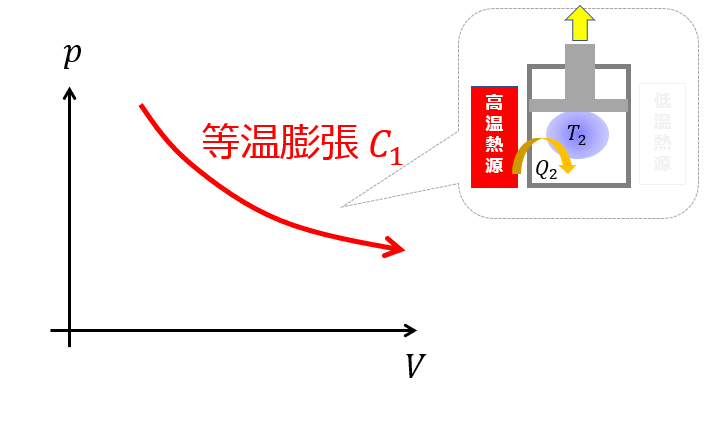

これをステップ1としておきます。
次に、サイクルを作るためには元の状態に戻さないといけません。
この元への戻し方はいろいろ考えられるかもしれません。
例えば・・・・
(ステップ2)温度を一定にしておいて(等温)で熱を取り去って元の状態へ戻します。
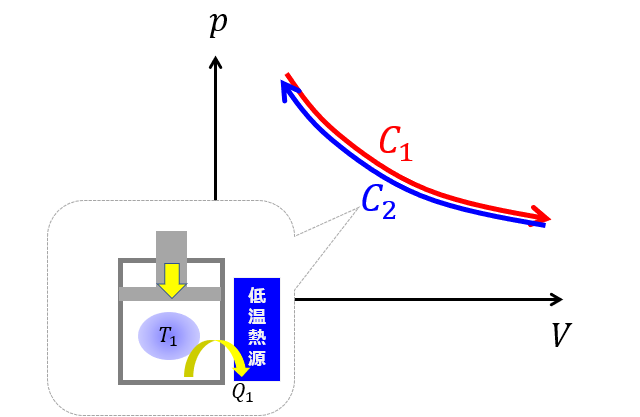

ここで感の良い人は気づくでしょう!
ステップ1でせっかく熱量を加えたのに、同じだけの熱量をステップ2で取り去っているではないですかと・・・
p-V図を見てください。
- 元の状態に戻すのに熱量の全てを仕事にしたと思ったら、元の状態に戻すのに加えた熱量と同じだけ熱量を取り去らなければなりませんでした・・・
もしくは、
- 加えられた熱量でせっかく仕事をしたのに、仕事をしてもらった分だけ元に戻すのに仕事を外からしなければなりませんでした・・・
というわけです。
めちゃくちゃ効率が悪いと思いませんかね。
このように、加えた熱量を効率良く仕事に変換するには「p-V図の面積」ができるだけ大きくなるようなサイクルを考えることが重要であることがおわかり頂けたでしょう。
単純なサイクルを考えただけではとても非効率なエンジンサイクルとなってしまうのです。
では、カルノーサイクルの場合を見てみましょう。
カルノーサイクル
「カルノーサイクル」の理解を深めるために、
- 各過程がなぜ必要なのか?
- 熱力学第一法則で理解するとどうなるのか?
を意識しながら理解を深めていきます。
※「熱力学第一法則」が怪しい方は↓こちらの記事をお読みください。
熱力学第一法則
Q=\Delta U +W\tag{1}
\end{align*}
という書き方にしておきます。
- \(Q\):与えた熱量
- \(\Delta U\):内部エネルギー変化
- \(W\):系(気体など)が外へした仕事量
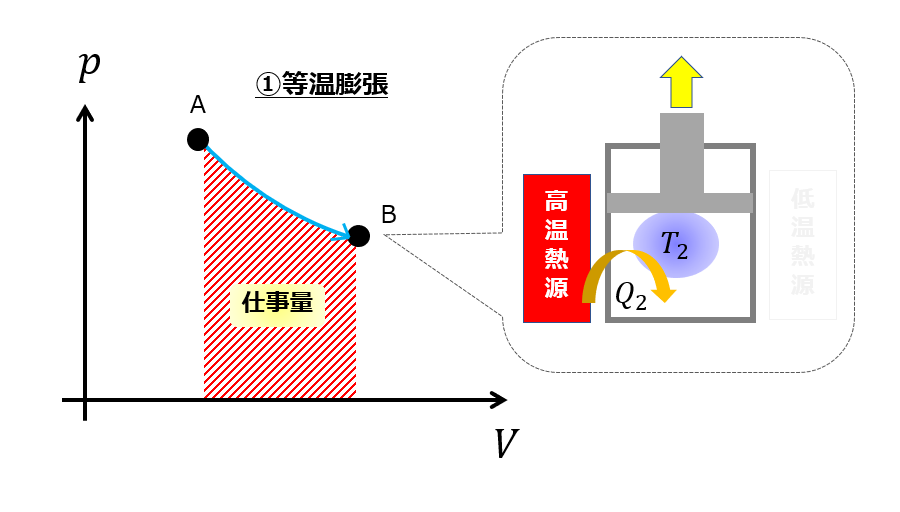
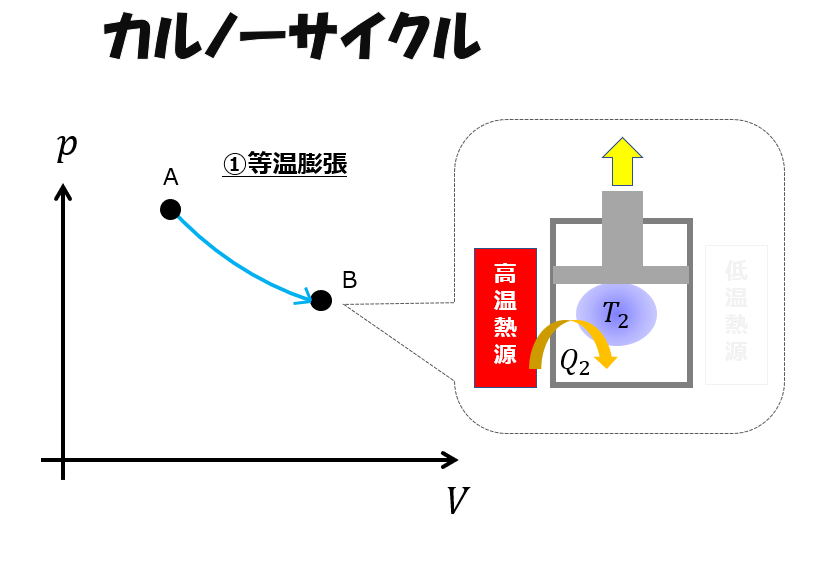
等温膨張(A⇒B)
カルノーサイクルの第一ステップはではシリンダーを高温熱源に接触させておいて膨張させます。
つまり、熱量\(Q_{2}\)を加えることで外へ仕事をします。

熱力学第一法則
Q_{2}=\Delta U_{AB} +W_{AB}\tag{2}
\end{align*}
与えられた熱量\(Q_{2}\)は、内部エネルギーの変化\(\Delta U_{AB} \)と外へする仕事へ分配されるます。
系が外部へした仕事は「p-V図」の面積です。
W_{AB}=\int_{AB}pdV
\end{align*}
仕事量としては「プラス」ですね。
理想気体の内部エネルギーは温度にのみ依存します。
今回のように体積が膨張しても温度が変わらないような過程(等温膨張)の場合では、内部エネルギーは変わりません。
つまり理想気体であれば、\(\Delta U_{AB}=0\)なので、
Q_{2}= W_{AB}\tag{3}
\end{align*}
となっています。
与えた熱量が全て仕事に使っているわけですね。
※理想気体というのは特別な場合です(3)式の結果になります。
ちなみにこの時点では、当然常温(20℃くらい)よりも高い温度で熱源に接触させているので、内部の圧力は大気圧よりは大きいでしょう。
重要な2つのステップ
ここから重要な2つのステップを踏むことになります。
- 断熱膨張(B⇒C)
- 等温圧縮(C⇒D)
この2つのステップがとても重要なのです。
先ほど示したように「役に立たないサイクル」で考えたように、何も考えずに元の状態に戻そうと思うと同じ仕事量だけ外から仕事をしてやらないといけません。
なぜ、同じ仕事量を外からしなくてはいけないのでしょうか?
それは、内部エネルギーが元に戻すための仕事を邪魔しているからです。
内部エネルギーは、内部(例えば気体など)でのエネルギーを意味しており力学でいう圧力を作るポテンシャルを持っています。
要するに、内部からの圧力があるから元に戻すのに邪魔になっていて外から結構な仕事量をしないと元通り(サイクル)に戻ってくれないというわけです。
では、できるだけ仕事をせずに元の状態に戻すためにはどうすれば良いでしょうか?
元に戻すのために、できる限り圧力低くすればよい!
ということですね。
圧力を下げるための方法、さっと思いつくのが「断熱にして体積を増やす」「温度を下げる」の2つでしょう。
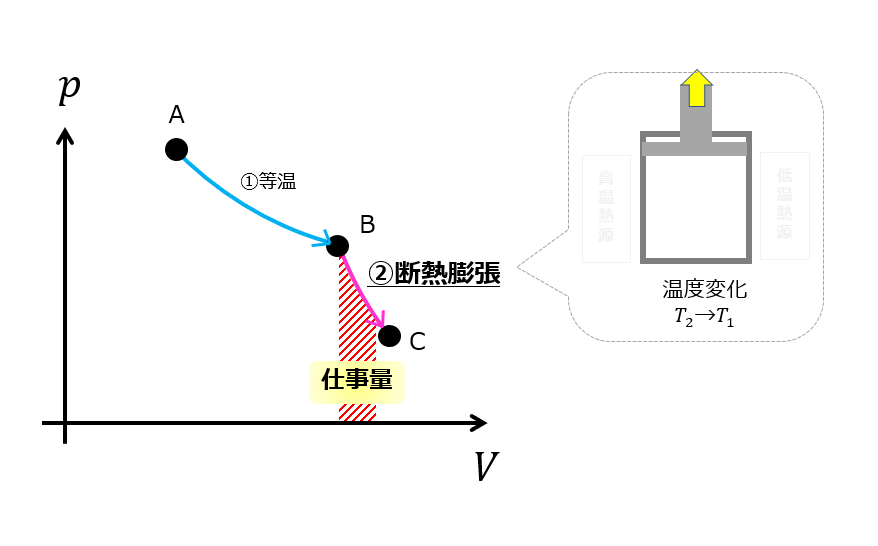
断熱膨張(B⇒C)
「等温膨張(A⇒B)」の過程で高温熱源に接触させていたので内部の圧力は大気圧よりは大きいでしょう。
するとうまいこと圧力を下げる方法があります。
断熱にして内部に溜まっている内部エネルギーを使って自然に膨張させてやります
これが「断熱膨張」です。
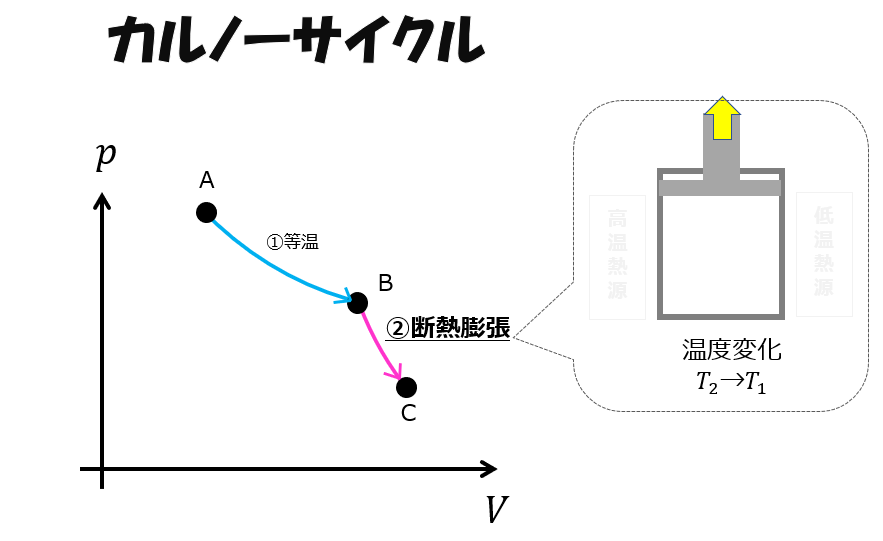

一般には等温膨張より断熱膨張の方が傾きがきついです。
- 等温変化:\(pV=const\)
- 断熱変化:\(pV^{\gamma}=const\)
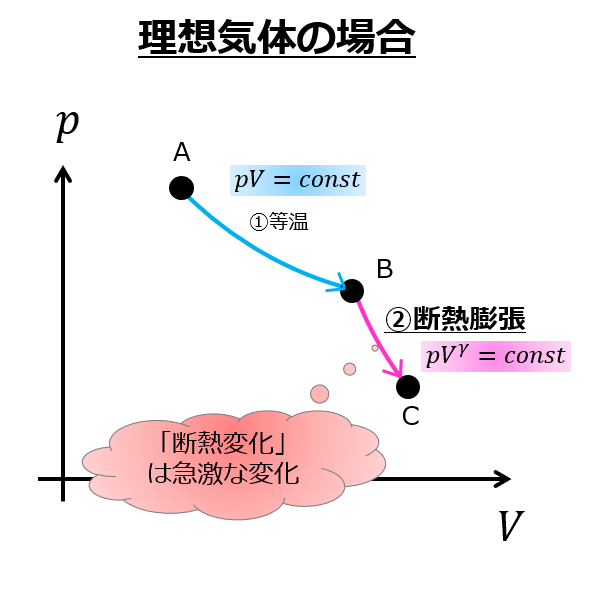

ですので、断熱変化の方が体積変化に対する圧力の変化が急激であることがわかります。
これは、断熱変化だと仕事量が直接内部エネルギーの変化につながるためです。
つまり、断熱変化というのは
- 圧縮させるときには急激に圧力を上昇させる方向になる
- 逆に膨張させるときは圧力が急激に下がる
圧力をできるだけ下げたいという意志に対してこの工程はとても理にかなっていますね。
断熱なので熱量の出入りは0(\(Q=0\))です。
熱力学第一法則
0=\Delta U_{BC} +W_{BC} \tag{4}
\end{align*}
つまり、内部エネルギーの変化量\(\Delta U_{BC} \)は外へする仕事\(W_{BC} \)へ変えることができます。
系が外部へした仕事は「p-V図」の面積です。
W_{BC}=\int_{BC}pdV
\end{align*}
仕事量としては「プラス」ですね。
「断熱膨張」という工程は、仕事量を産み出す実に効率の良い方法ですよね。
外へ仕事をさせつつ、同時に内部エネルギーを下げることができました。
内部エネルギーが下がっているということは温度も下がっているということになります。
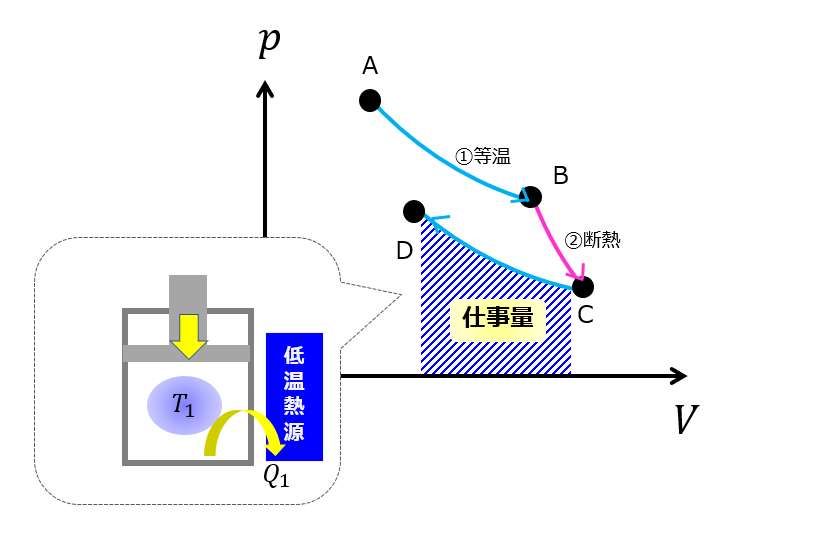
等温圧縮(C⇒D)
次に、大事なステップである「等温圧縮」にいきます。
先ほど、「p-V図」の面積ができるだけ大きくなれば熱を効率よく仕事に変えることができている状態であると説明しました。
断熱膨張(B⇒C)を終えた時点で、内部の圧力も温度も下がっているので、元の状態に戻すのは楽であります。
もっと効率よくもとの状態に戻すために「等温圧縮(C⇒D)」をはさみます。
低温熱源に接触させて体積を小さくしていくように外から仕事を加えます。
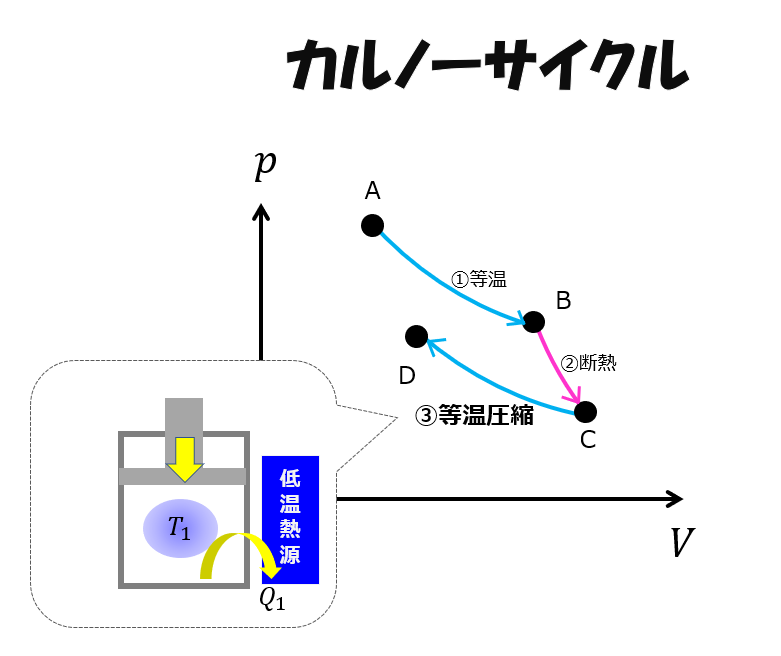

このとき、温度が一定になるようにしています。
「断熱膨張(B⇒C)」と「等温圧縮(C⇒D)」の2つの工程を使うことで、先ほど説明した”役に立たないサイクル”と違ってサイクルが囲む面積がゼロでなくなっています。
非常に重要な知見を得ることができました。
低温熱源があるおかげで、熱のすべてではないけどサイクルの中で意味のある仕事量を取り出すことができます。
熱力学第一法則
-Q_{1}= \Delta U_{CD}+W_{CD}\tag{5}
\end{align*}
系が外部へした仕事は「p-V図」の面積です。
W_{CD}=\int_{CD}pdV
\end{align*}
仕事量としては「マイナス」ですね。
理想気体であれば、\(\Delta U_{CD}=0\)なので、
-Q_{1}= W_{CD}\tag{6}
\end{align*}
となっています。
つまり、外から仕事をした分だけ熱を放出していることになります。
でも、「断熱膨張(B⇒C)」の過程で圧力を下げてくれたおかげで元の状態にもどすのに仕事をさほど必要としていません。
これは「等温変化」が「断熱変化」よりもp-V図で緩やかな変化をしてくれているおかげです。
この何気ない低温熱源がとても重要なのです。
むしろ、この低温熱源がないと絶対に元の状態に戻ることはできません。
断熱圧縮(D⇒A)
元の状態に戻すというのは、元の状態量に戻すことを意味しています。
つまり、温度、圧力、体積・・・など熱力学的な状態量が元に戻す必要があるのです。
ということは、温度を元に戻さないといけません。
ここで、元の温度に戻すために断熱なので熱量の出入りは0(\(Q=0\))です。
熱力学第一法則
0= \Delta U_{DA}+W_{DA}\tag{7}
\end{align*}
系が外部へした仕事は「p-V図」の面積です。
W_{DA}=\int_{DA}pdV
\end{align*}
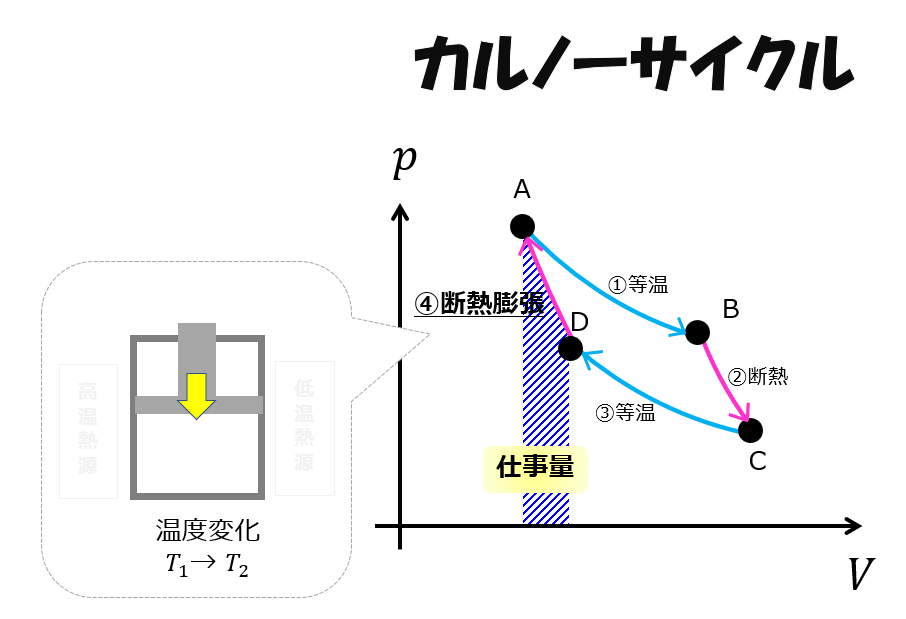

この一連のサイクルがカルノーサイクルです。
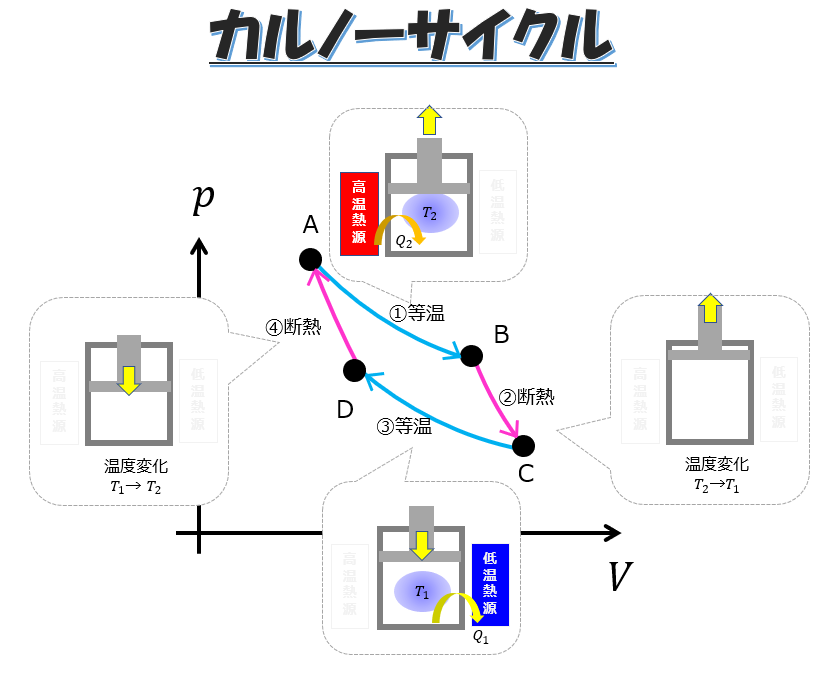


低温熱源が重要な役割
カルノーサイクルにおいてサイクルのステップにおいて、
熱を捨てるという工程を踏まなければならない・・・
ということがわかりましたね。
このことが、「サイクルにおいて熱のすべてを仕事に変えることはできない」という事実につながります。
- 熱力学第二法則
- 低温熱源の存在
熱効率は?「熱」を「仕事」にどれだけ変えることができたか?
熱効率を計算してみましょう。
熱効率は「サイクルの中で与えた熱をどれだけ仕事に変えることができたか?」
それを以下のように定義します。
\eta = \frac{W}{Q_{2}}\tag{8}
\end{align*}
- \(Q_2\):与えた熱量
- \(W\):正味の仕事量(p-V図で囲まれた面積)
\left\{\begin{matrix}
等温膨張(A→B):Q_{2}&=&\Delta U_{AB} +W_{AB}\\
断熱膨張(B→C):0&=&\Delta U_{BC} +W_{BC} \\
等温圧縮(C→D):-Q_{1}&=& \Delta U_{CD}+W_{CD}\\
断熱圧縮(D→A):0 &=& \Delta U_{DA}+W_{DA}
\end{matrix}\right.
\end{align*}
全て足すと・・・
Q_{2}-Q_{1}= &\Delta U_{AB}+\Delta U_{BC} +\Delta U_{CD}+\Delta U_{DA} \\
&+W_{AB}+W_{BC}+W_{CD}+W_{DA}\tag{9}
\end{align*}
ここで、内部エネルギーというのは「状態量」なので元の状態(AとDが同じ状態)になっているので、サイクルの最初と最後で内部エネルギー変化はありません。
\Delta U_{AB}+\Delta U_{BC} +\Delta U_{CD}+\Delta U_{DA} =0\tag{10}
\end{align*}
では、系が外部にした仕事量\(W_{AB}+W_{BC}+W_{CD}+W_{DA}\)はというと・・・
p-V図の囲まれた面積です。
これを「系が外部にした正味の仕事量」として\(W\)と置くと、
W=W_{AB}+W_{BC}+W_{CD}+W_{DA}\tag{11}
\end{align*}
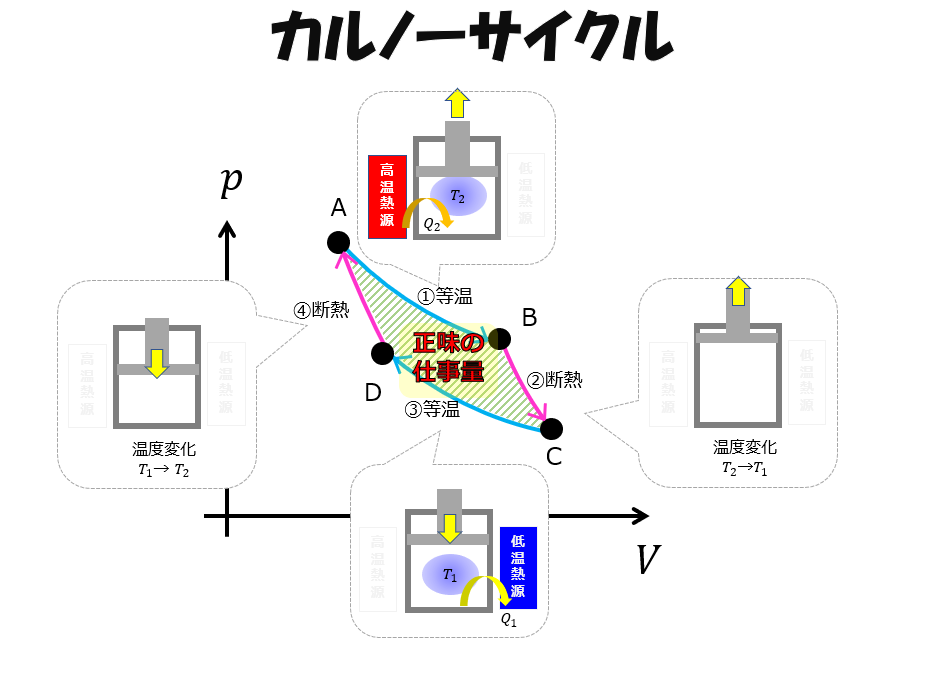

となります。
だから、
「与えた熱量をどれだけ仕事に変えることができたか」という効率は、
\eta = \frac{W}{Q_{2}}\tag{8}
\end{align*}
もしくは((10)式も使って)、
\eta = \frac{Q_{2}-Q_{1}}{Q_{2}}=1-\frac{Q_{1}}{Q_{2}}\tag{12}
\end{align*}
となります。
カルノーサイクルを単純化する
カルノーサイクルを単純に表現すると「高温熱源から熱\(Q_{2}\)をもらって、仕事量\(W\)を行い、低温熱源に熱\(Q_{1}\)を捨てるサイクル」です。
これを、☟右の絵のように表現するととてもわかりやすいです。
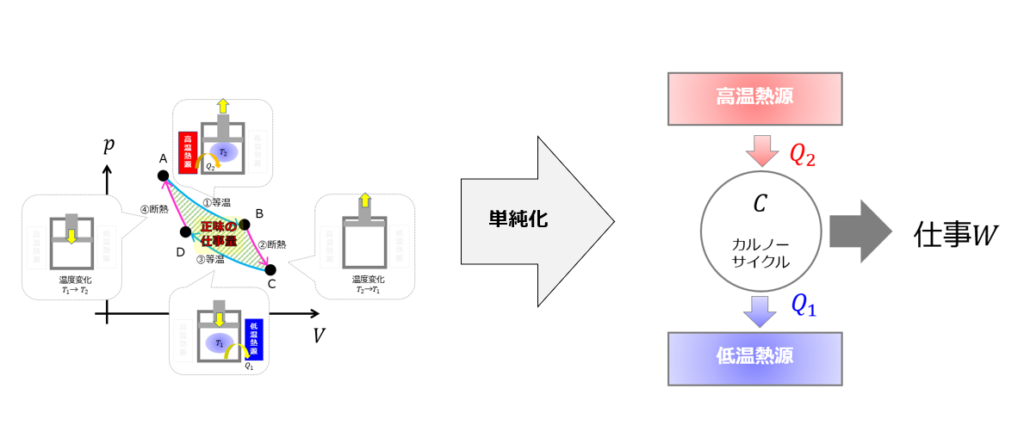

熱をもらって、熱を捨てているサイクルであることがよくわかるようになりました(^^)/
まとめ
本記事では、カルノーサイクルについて解説をしました。
大事なポイントは以下です。
- カルノーサイクルは「熱を仕事に変える最大効率のエンジンサイクル」
- 低温熱源の重要性:熱を捨てるという工程を踏まなければならない。
- 「与えた熱量をどれだけ仕事に変えることができたか」という効率は、
\eta = \frac{W}{Q_{2}}\tag{8}
\end{align*}
もしくは((10)式も使って)、
\eta = \frac{Q_{2}-Q_{1}}{Q_{2}}=1-\frac{Q_{1}}{Q_{2}}\tag{12}
\end{align*}
「1.カルノーサイクルは「熱を仕事に変える最大効率のエンジンサイクル」について詳細に解説することができませんでした。
次回の記事で解説したいと思います。
お勧めの参考書
熱力学の理解のために是非読んでほしい参考書を3つ紹介します。
こちらの参考書はカルノーサイクルについてとても詳しく解説がされている良書です。
主に、熱力学第二法則やエントロピーについての解説が歴史的な流れから解説されていて「エントロピーの概念ってどうやってできたの?」っていうのが気になる方は絶対読んだ方がいいです(^^♪
この2冊は熱力学を学ぶ人にとっては鉄板の2冊だと思います。
一味違う熱力学の魅力を感じることができる書籍ですので、是非手にとってじっくりと味わいながら熱力学の魅力を味わってほしいです。