こんにちは(@t_kun_kamakiri)。
本記事では、熱力学第二法則というのを話していきます。
タイトルの通り「わかりやすく」と自身のハードルを上げているのですが、わかりやすいかどうかは日常生活に置き換えてイメージできるかどうかにかかっていると思っています。
熱力学第二法則と言ってもそれに関連する法則はいくつもの表現がされています。
少し列挙しておきましょう！（7つ列挙！！）
- クラウジウスの原理
- トムソンの原理（ケルビンの原理）
- カルノーの原理
- 第二種永久機関は存在しない
- 熱と仕事は非対称
- クラウジウスの不等式
- エントロピー増大則
全部は説明しきれないので、本記事では以下の内容に絞って書いていきます。
- クラウジウスの原理
- トムソンの原理（ケルビンの原理）
- カルノーの原理
- 第二種永久機関は存在しない
- 熱と仕事は非対称
の解説をします(^^♪
関連する法則が7つあったり・・・結局何を覚えておくのが良いのかわかりずらいもの熱力学第二法則の特徴のひとつです。
ご安心を(^^)/
全部、同値な法則なのです。
まずは、熱力学第二法則を理解する2つの質問を用意しましたので、そちらに答えるところから始めよう！
「熱力学第二法則」を理解するための2つの質問
以下の2つの質問に答えることができたら、熱力学第二法則を理解したと言っても良いでしょう(^^)/
湯たんぽにお湯を入れます。
その湯たんぽを放置しているとどうなりますか？
自然に起こるのはどちらですか？
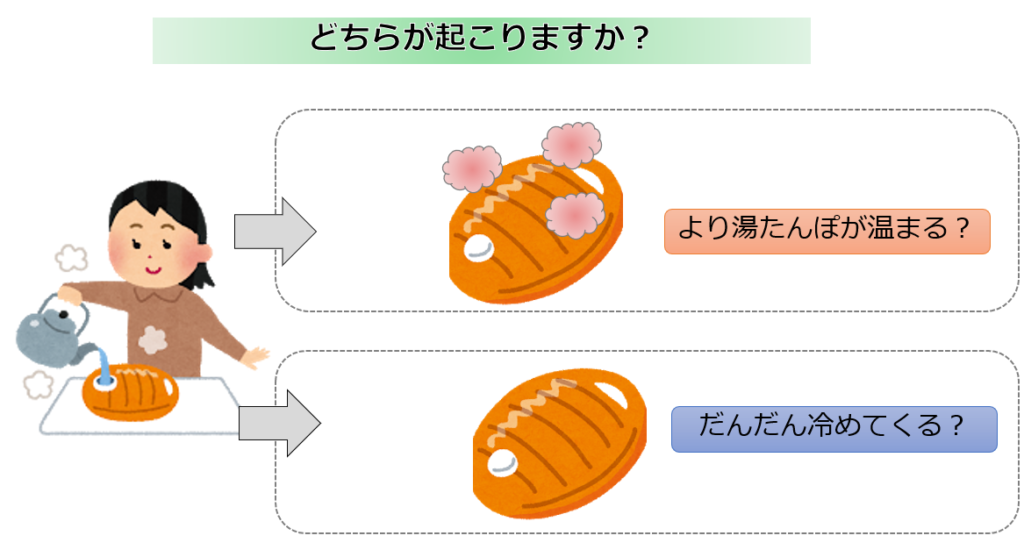
【正解】
だんだん冷めてくる(‘ω’)ノ
【解説】
熱量は熱いものから冷たいものへ移動するのが自然に起こる！
（その逆はない）
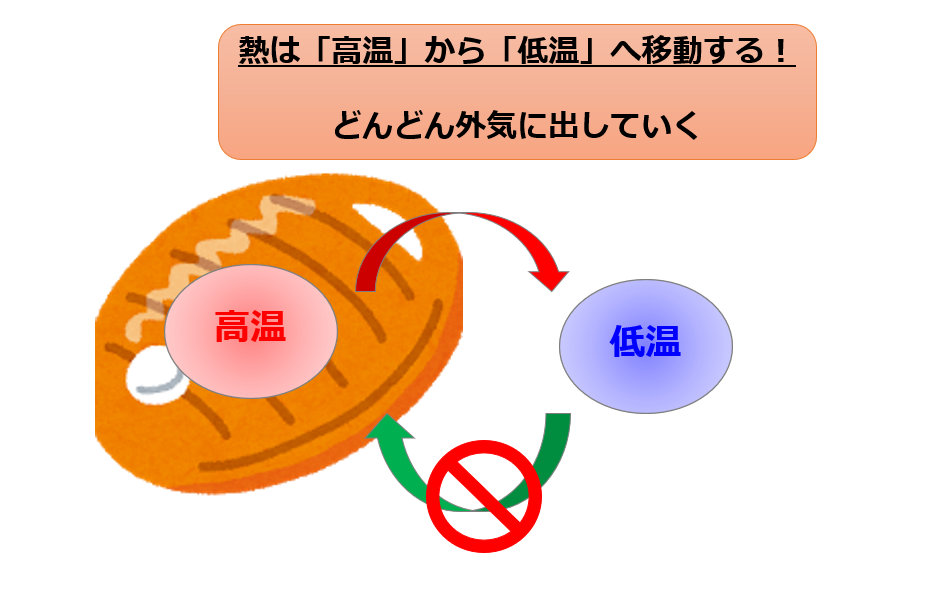
このように、誰もが感覚的に知っているように「熱は温度が高いものから低いものへ移動する」という現象が、熱力学第二法則です。
熱の移動の方向を示している法則なのです。
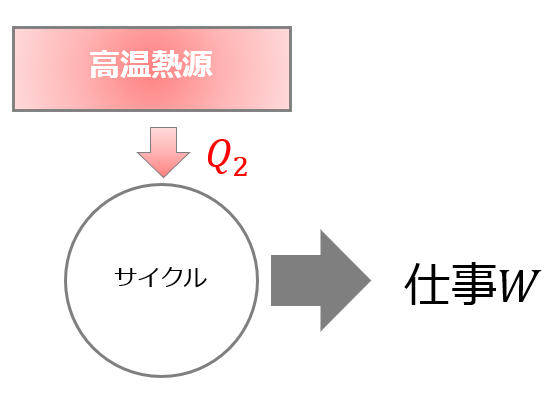
熱量の全てを仕事に変えるようなサイクルは作ることができるのか？
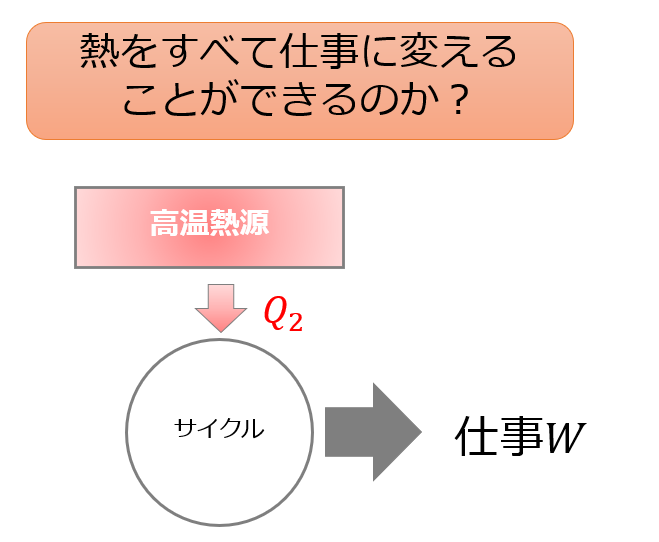
【正解】
できない。
【解説】
$\eta=\frac{W}{Q_2}=1$は無理という事です。
どんなに工夫をしても、熱の全てを仕事に変えるようなサイクルは実現できないということが明白になっています。
こちらも熱力学第二法則です。
現代の電力発電所でも効率は40%程度と言われています。
熱量を加えてそれをすべて仕事に変えることができたら、車社会においてめちゃくちゃ効率の良いエンジンができますよね。
車のエンジンでも瞬間的に温度が3300K以上となって、1400Kあたりで排出すると言われていますので効率は理論上でも50％程度・・・・しかし、現実には設計限界などがあって、25%程度になるそうです。
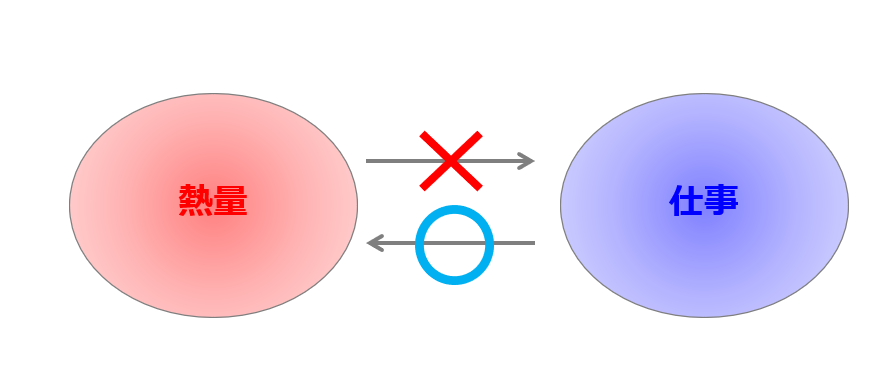
熱エネルギーと仕事エネルギー・・・同じエネルギーでも、「仕事をすべて熱に変えることができる・・・」が、「熱をすべて仕事に変えることはできない」という法則も熱力学第二法則です。
エネルギーの質についての法則なのです！
超ざっくりまとめると熱力学第二法則とは
【超ざっくり熱力学第二法則の説明】
- 熱の移動は「温度の高い方」から「温度の低い方」へと移動するのが自然。
その逆は起こらない。 - 熱をすべて仕事に変換するエンジンは作れない。
というようにまとめることができます。
少々言葉足らずなところがありますが、日常生活に置き換えて理解するのには余計な言葉を付けると逆にわからなくなってしまいますので、まあ良いでしょう。
（よく「ほかに何も変化を残さずに・・・」という表現がかかれているのですが、最初は何言ってるのかわかりませんでした・・・そのあたりも解説を付けたいと思います。）
ここまでで何となく理解したって思ってもらえればOKです。
これより先は少々込み入った話になりますが、上記の2つの質問に立ち返って読んでもらえればと思います(‘ω’)
なぜ、熱力学第二法則が必要なのか？
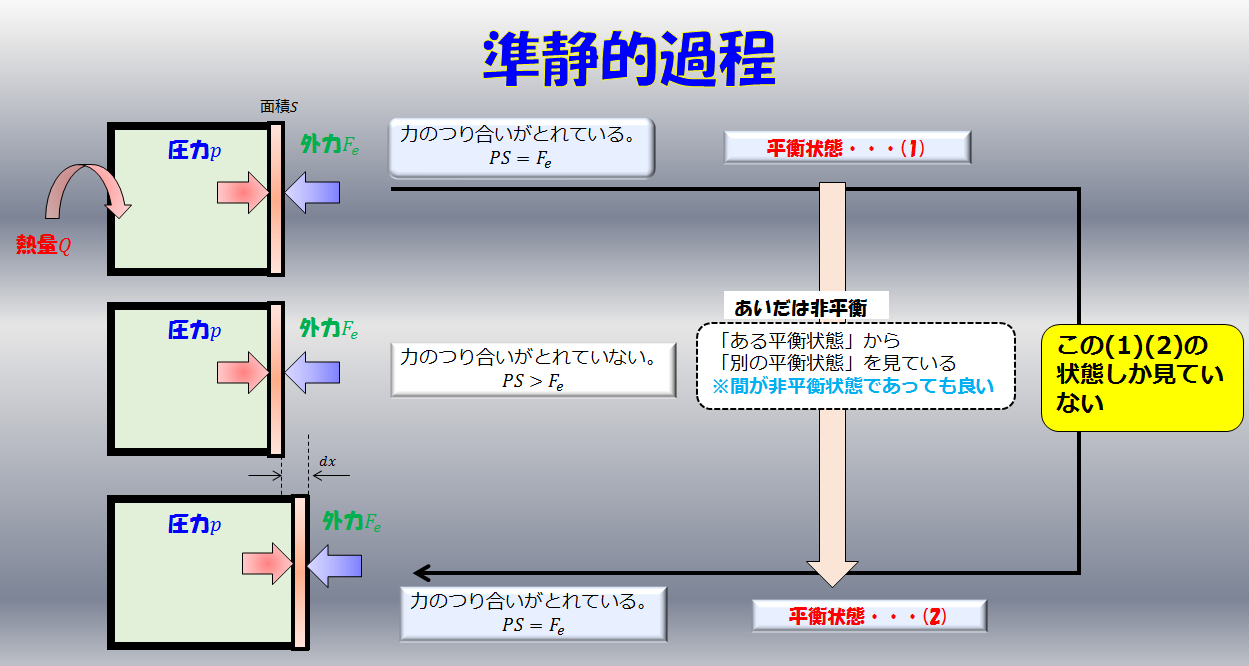
熱力学は「平衡状態」から「別の平衡状態」への変化を記述する学問であります。
熱力学第一法則だけで十分ではないかと思うかもしれませんが、熱力学第一法則を満たしていても（エネルギーが保存していても）、
- 何から何への変化が自然に起こるのか？
- 自然界でその変化は起こるのか、起こらないのか？
その区別をしてくれるものではなりません。
これらの区別を与える基準になる法則が、熱力学第二法則なのです。
そう思ったときに登場するのが、エントロピーです！
エントロピーという名前は、専門用語すぎるにも関わらず結構知られている概念です。
「その変化は自然に起こるのかどうか・・・？」を定量的に表現するためのエントロピーという量です。
エントロピーは、「不可逆性の度合」「乱雑さの度合い」など実にわかりにくい意味合いで説明されていますが、エントロピーは個人的には「その変化は自然に起こるのかどうか・・・？」を評価してくれる量であるのが熱力学でのエントロピーの意味だと思っています。
エントロピーについて話し始めるとそれだけで長くなりそうなのでここでは、割愛します_(._.)_
勉強が進んだら記事にします！
これらの法則が疑いもしない原理として認めて、「エネルギーは保存しているけど、自然に起こりうる状態とは何か？」というのを知見を与えてくれるとってもありがたい経験事実だってことですね(^^)/
こんなにいっぱい「法則」「原理」と名の付くものがありますが、実はすべて等価な意味を表しているのです。これらのうちひとつでも認めない（嘘だった）とすれば、たちまち他の全ての法則も嘘だったという事になります。
※ちなみに「原理と法則」って何が違うの？って思ったけど、同じでした。
「原理」と「法則」の違い。
「トムソン」と「ケルビン」の違い。☟（使用例）熱力学第二法則
✅クラウジウスの法則
✅トムソンの法則
✅カルノーの原理
✅ケルビンの原理
✅第二種永久機関は存在しない
✅熱と仕事は非対称
✅クラウジウスの不等式
✅エントロピー増大則※結論、違わない。 pic.twitter.com/VAORbNEDTT
— カマキリ🐲@物理ブログ書いている (@t_kun_kamakiri) 2020年4月24日
では、さっそくこれらの法則をさらっと見てみることにしましょうかね(^^)/
クラウジウスの原理
これがクラウジウスの原理です。
絶妙にわかりにくく表現されているので、ひとつひとつ見ていくしかないのがやっかいですが・・・ひとつひとつ見ていきます。
- 後半部分の「熱を低温の物体から高温の物体に移すことはできない」
熱の移動は高温から低温に移るというのが自然であって、低温から高温に移そうと思ったら何か外から手を加えないといけないよってことです。
これははわかりやすいですね。
- 前半の「他に何も残さずに」という条件が付いています。
ここが、この法則のミソなのです。
「他に何かを残す」という表現がまずわかりにくいので、何か外から仕事を加えて状態が変わってしまう（体積が大きくなるとか）と思っておけば良いでしょう。
低温から高温へ熱を移そうと思ったら何か仕事を加えるなりしないと無理だよっていうことを言っているようです。
逆に、高温から低温へ熱を移そうと思ったら、それについては言及していません。
わかりやすい例で言うと、
- 「お湯の入った湯たんぽを放置していると、何もしていなくてもだんだん冷めてくる（より温まることはない）」、
- 「熱い部屋の熱を外へ逃がそうと思ったら、それなりに何か手を加える必要がある」
ってことです(‘ω’)ノ
だからクラウジウスの原理というのは、「”自然には”熱は温度が高いものから低いものへ移動する」という現象をじゃっかんわかりずらく表現しているだけでしたね。
誰もが感覚的に知っているように、「湯たんぽは冷めるんだ。熱は高温から低温に移るのが自然なんだ」ってことです。
熱の移動の方向を示している法則なのです。
トムソンの原理（ケルビンの原理）
これがトムソンの原理です。
クラウジウスの原理よりもっと理解が難しくなっています。
詳しく説明するしかないです(;^ω^)
前回の記事でカルノーサイクルについて解説しましたが、こちらの記事に関連した内容ですので一度お読みください。
☟カルノーサイクルとは「高温熱源から熱\(Q_{2}\)をもらって、仕事量\(W\)を行い、低温熱源に熱\(Q_{1}\)を捨てるサイクル」です。
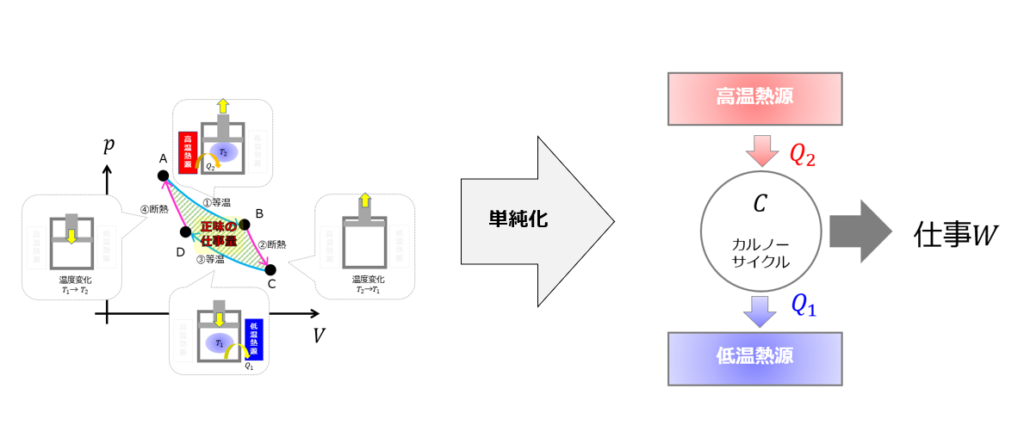
熱をもらって、熱を捨てているサイクルです。
与えた熱$Q_1$のうちどれだけ仕事$W$に変えることができたのかという効率、
\eta = \frac{Q_{2}-Q_{1}}{Q_{2}}=1-\frac{Q_{1}}{Q_{2}}
\end{align*}
は\(\eta\)は必ず１より小さいです・・・・
よく考えたら、この捨ててる熱\(Q_{2}\)が無駄だから、熱効率が１にならないのですよね・・・・でも熱\(Q_{2}\)を捨てなければ、元の状態に戻ることができずサイクルを作ることができないというのが、トムソンの原理なのです。
☟これは不可能という事です。
「他に何の変化も残す」や「サイクル」ならば実現は可能
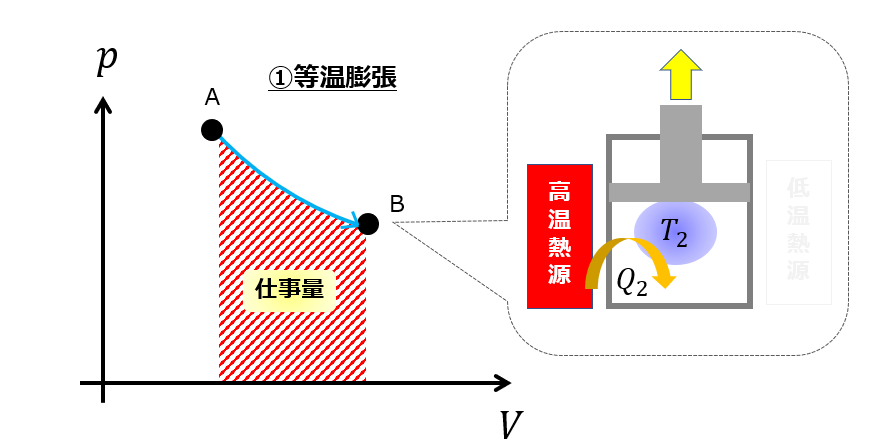
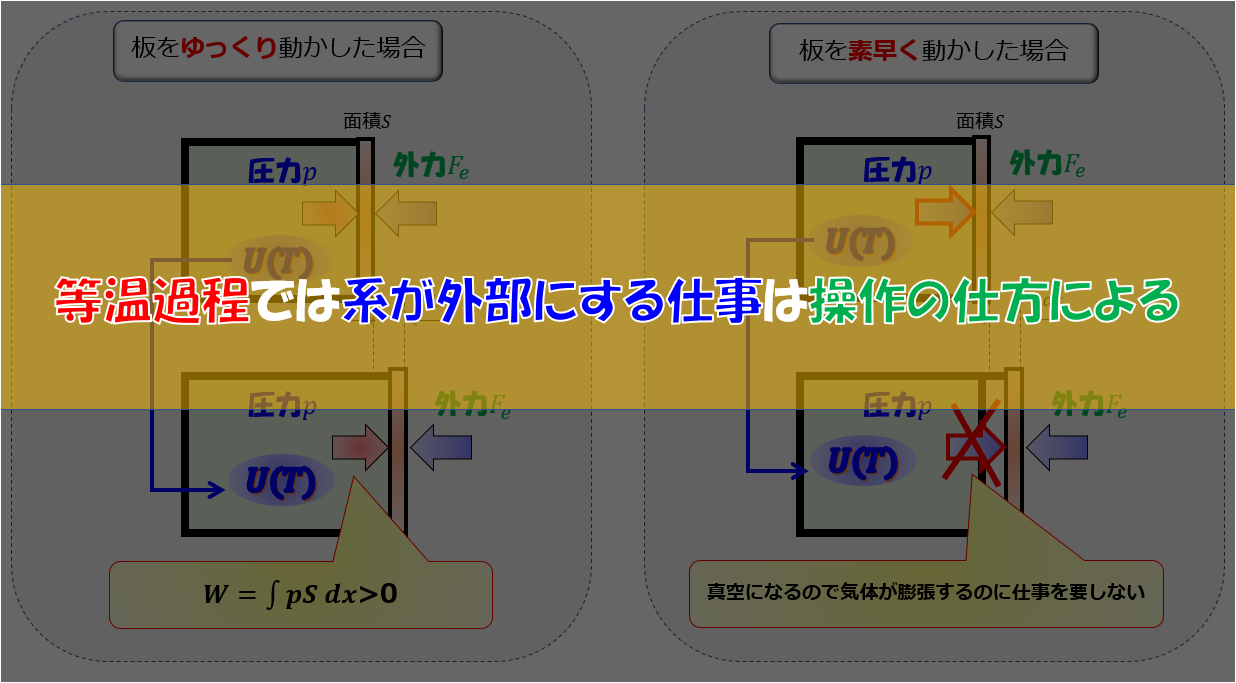
カルノーサイクルの一部である「等温膨張」なんてまさにそうですよね。
熱力学第一法則を考えると、
Q_{2}=\Delta U_{AB}+W_{AB}
\end{align*}
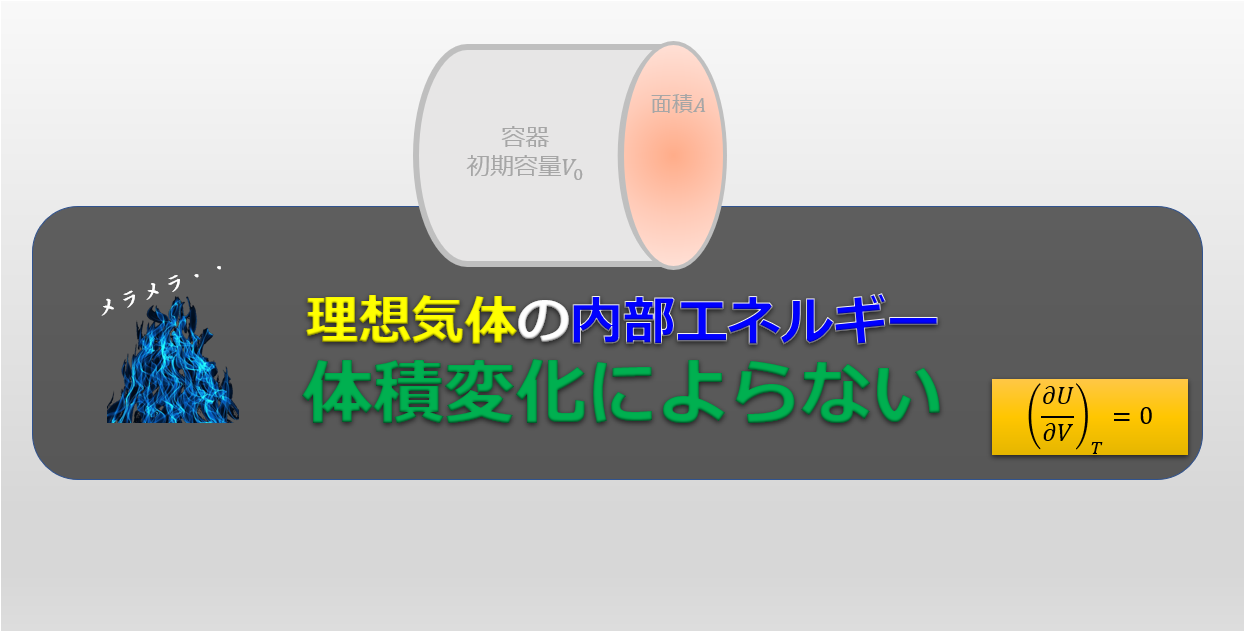
理想気体で考えると、内部エネルギーは温度のみに依存するので温度が変わらなければ内部エネルギーは変わりません。
だから、等温過程なら$\Delta U_{AB}=0$なので、
Q_{2}=W_{AB}
\end{align*}
となり、熱の全てを仕事に変えることができます。
が、全然元の状態に戻ってないですよね。
「他に何の変化も残さず」という表現を使っているのは、明らかに熱機関であるサイクルを意識した表現であることがわかるかと思います。
このように、「熱の全てを仕事に変えて、もとの状態に戻るような周期的な運動をする装置は作れない！」ということです。
だから、カルノーサイクルのようにサイクルを作ろうと思うと、1つの熱源だけでは実現することができず、熱を捨てるための低温熱源が必ず必要であるというのがトムソンの法則の意図するところでもあります。
「それはできる！」と言って、「ほらできた！」というのは形にできますが、
「それはできない！」と言って、どうやって証明しようかって思うのがふつうです。
熱を捨てないと絶対に周期運動する熱機関を作れないって言ってくれると諦めがつきますよね。
いや、本当はできるかもしれませんが、過去の先人たちが何をやっても実現しなかったので「諦めて原理にしやったよ_(._.)_」って話なのかもしれませんが、理論とはそんなものです(笑)
「何かを認めてる。そして、認めたものから何を予測できるか？」という姿勢がとても重要で、トムソンの法則というものを認めてしまっているのです。
熱だけでどれだけ仕事量を増やそうとしても、無理なものは無理ってきっぱり言ってくれているので清々しいです(‘◇’)ゞ
きっぱり諦めて認めよう！！
第二種永久機関は存在しない
第二種があるなら、第一種があるものですよね。
第一種永久機関というのは、「無のエネルギーから永久に外部に仕事をしてくれる装置」のことです。
もう、見るからにエネルギー保存則に反していて不可能であることはわかりますが、第二種永久機関はどうでしょうか？
まずは、第二種永久機関の定義についてです。
このような機関は実現できないよってことです。
正の熱を与えてくれる熱源ばっかりで、それを全部仕事に変えることはできないってことです。
これも、熱と仕事は等価な価値を持っていないというのと同じです。
第二種永久機関はできそうでできない・・・・
例えば、まわりの環境はとても大きいので、熱源からの熱量を全て仕事に変えることができたとしても、元の状態に戻すためには必ず熱を逃がさないといけないと先ほど言いましたが、まわりの環境が膨大なので逃がした熱は周りの環境になじんでしまってまた逃がしたつもりでも逃がしてないのと同じなので、また膨大な環境による熱源から熱をもらえば半永久的に仕事を行える・・・・
ように見えるが、これが効率$\eta=\frac{W}{Q}=1$になっていないので、できそうでできていないという事になります。
なぜ効率$\eta=\frac{W}{Q}=1$にならないのか？
「他に何も残さずに、熱を低温の物体から高温の物体に移すことはできない」というクラウジウスの原理を認める限り、無理なものは無理という事になります(笑)
クラウジウスの原理とトムソンの原理は同値であり、どちらかを認めれば必ずどちらかも認めざるを得ないし、
仮にどちらの原理が間違っているとすれば、たちまち2つとも間違った原理になります。
第二種永久機関の存在の否定は、この原理がある限り装置として「絶対無理だよ！」って言われている、なんともかわいそうな装置だったという事です(‘ω’)ノ
※ちなみに第二種永久機関の特許を出しても、今は門前払いされるそうです(笑)
熱と仕事は非対称
トムソンの原理で「熱の全てを仕事に変換できない」と言っていますが、仕事の全てを熱に変えることはできます。
例えば以下のように、
- ステップ１：断熱容器内と外気温度$T_{e}$は同じにしておく(熱平衡状態）
※断熱容器は断熱材で容器を覆うなどしておく。 - ステップ２：外から仕事$W_e$をして内部エネルギーを高める。
※このとき内部エネルギーは温度の増加関数なので温度も上昇している（$T_1>T_e$）
熱力学第一法則から$U_0+W_e=U_1$ - ステップ３：断熱材を取っ払う。
そうすることで、高温から低温（外気）に向かって熱が移動するため容器内の内部エネルギーは下がる。
熱力学第一法則から$U_1-Q_e=U_0$となって、内部エネルギーは元の状態に戻る。
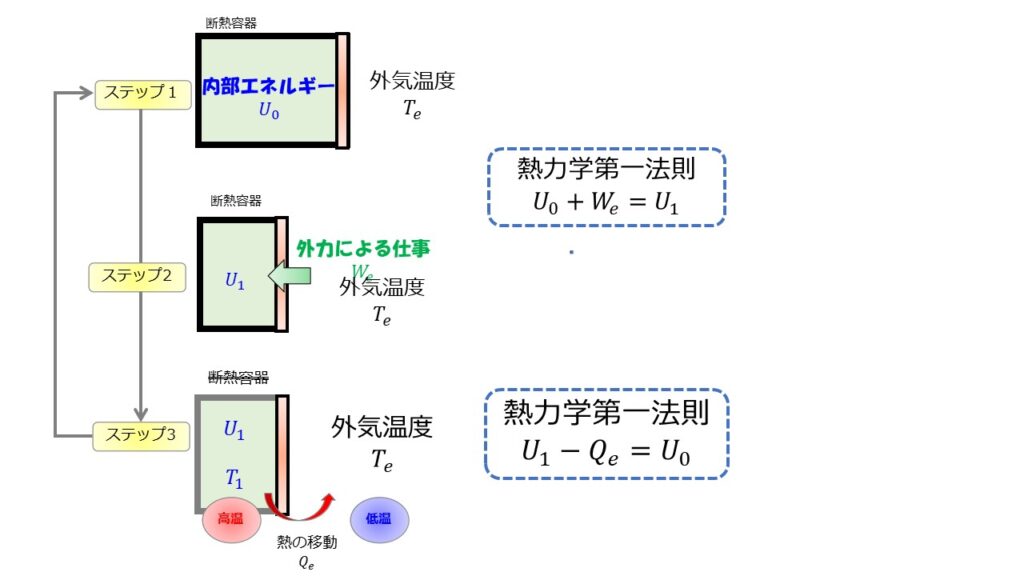
このようにすることで、
U_0+W_e&=&U_1\\
U_1-Q_e&=&U_0
\end{align*}
より、辺々を足して・・・
W_e=Q_e
\end{align*}
となるので、仕事を全て熱量に変えることができます。
容器の大きさを元に戻そうと思ったら、もう一度断熱材で容器を囲って容器の体積を元に戻すように仕事をして、その後放置していれば熱平衡状態になって外気と同じ温度になるでしょう。内部エネルギーは温度の関数で一意に決まるので、完全に元の状態に戻すことができます。
ここで言いたいのは以下の事です。
最初と最後の状態が全く同じになるような変化をしながら、
仕事を使ってすべてを熱に変えることはできるが、熱の全てを仕事に変えることはできない。
これがまさに熱力学第二法則での主張であります。
要するに、同じエネルギーでもエネルギーの質が違うのです。
熱エネルギーの方が使い勝手がわるくて、力学的な仕事量の方が使い勝手が良いのです。
だから、水を温めておいて何かのエネルギーに変えようと考えるよりも、高い位置に水を蓄えておく方が同じエネルギー量でも変換されたときの効率が
その他、電気エネルギーによって熱を産み出せても、熱によって電気を生むことができません。
このように、同じエネルギーでもエネルギーとしての質が異なるのがわかると思います。
まとめ
はじめて熱力学第二法則を学ぶ人は以下の2点は最低限覚えておく。
以下の、様々な熱力学第二法則の表現が同値であります。
最初と最後の状態が全く同じになるような変化をしながら、
仕事を使ってすべてを熱に変えることはできるが、熱の全てを仕事に変えることはできない。
お勧めの熱力学の参考書
熱力学の定番の2冊を紹介します。
本記事の内容である熱力学第二法則はエントロピーと深く関係している法則です。
Follow @t_kun_kamakiri