こんにちは(@t_kun_kamakiri)(^^)/
前回では「行列式の重要な性質」についての内容をまとめました。
今回は「逆行列とは何か?」について解説を行います。
- 逆行列とは何か?
- 余因子行列
- 逆行列の定義
結論から言うと、逆行列の定義は$A^{-1}=\frac{1}{|A|}\tilde{A}$と書けます。
ここで、$\tilde{A}$は余因子行列と呼ばれるものです。本記事でも余因子行列については詳しく解説をするのでご安心ください。
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事の内容をマスターして行列計算を楽に計算できるようになりましょう(^^)
逆行列とは
まずは、「逆行列って何?」「どう定義されるものなの」という疑問にお答えします。
例えば、スカラー量$a$に対しては、ある量$x$を掛けると1($xa=ax=1$)となる数がありますよね。このとき$x=\frac{1}{a}=a^{-1}$は$a$の逆数と言います。
このスカラーにおける逆数に相当する行列が「逆行列」ということわけです。
逆行列はスカラー量における割り算に相当するものだと考えてください。
$n$次正方行列$A$に対して$XA=AX=E$($E$は単位行列)となる行列$X$が存在するとき、$X$を$A$の逆行列と言い、$X=A^{-1}$と表します。
※行列には割り算の記法がないため$\frac{1}{A}$とは書きません。
逆行列はどんな行列でも存在するわけではなく逆行列が存在する条件というのがあります。
下記の記事で行列式の定義を解説をしましたが、逆行列が存在するかどうかの判断に本記事で扱う行列式が重要になってきます。
まず結論を以下に述べておきます。
\left\{\begin{matrix}
|A|\neq 0のとき& Aは正則\rightarrow 逆行列A^{-1}が存在する\\
|A|=0のとき & Aは正則ではない\rightarrow 逆行列A^{-1}が存在しない
\end{matrix}\right.
\end{align*}
さらに、行列式は任意の行列に対して存在するのではなく正方行列(行と列が同じ数の行列)のみ存在します。
以上の内容をまとめると
ということになります。
例えば2次正方行列$A$に対して、
A=\begin{pmatrix}
a_{11} &a_{12} \\
a_{21} &a_{22}
\end{pmatrix}
\end{align*}
しかし、2行3列の行列$A$に対しては
A=\begin{pmatrix}
a_{11} &a_{12} &a_{13} \\
a_{21} &a_{22} &a_{23}
\end{pmatrix}
\end{align*}
なぜ行列式$|A|$が0である場合に逆行列が存在しないのかと言うと、後で詳しく解説しますが逆行列の定義が以下だからです。
A^{-1}=\frac{1}{|A|}\tilde{A}
\end{align*}
※$\tilde{A}$は$A$の余因子行列
逆行列の定義の分母に行列式があるため、行列式が0だと逆行列が定義できないということですね。
まずは、正方行列かどうかで行列式が定義ができるかどうかを見て、行列式が0ではない場合に逆行列が存在するということですね(^^)
逆行列の求め方
ここからは、どうやって逆行列を求めるのかを解説します。
逆行列の求め方は1つだけではなく、主に以下の複数の方法があります。
- 余因子行列で表す
- クラメルの公式
- 掃き出し法
今回は余因子行列を使った方法で逆行列を求めてみます!
余因子行列は余因子展開を理解しておく必要があるので、お忘れの方は下記の記事で復習しておくことをお勧めします。
余因子展開は以下で定義されています。
|A|&\underset{j列目で展開}{=}a_{1j}\tilde{a}_{1j}+a_{2j}\tilde{a}_{2j}+\cdots +a_{nj}\tilde{a}_{nj}\\
&\underset{1つ目の添え字\\で和をとる}{=}\sum^{n}_{i=1}a_{ij}\tilde{a}_{ij}
\end{align*}
- $j$列に目ついて展開しているので添え字の2つ目は変わっていません。
- 行に対して和をとっているので添え字1つ目の数字が変わっています。
この2点が重要です。
※「列」で言えることは行で言えるため、「行」に対する余因子展開も定義できます。
今回逆行列で必要になるのは、余因子$\tilde{a}_{ij}$です。
余因子$\tilde{a}_{ij}$は、正方行列$A$に対して$i$行と$j$列を取り除いた行列式を作り下記のように定義します。
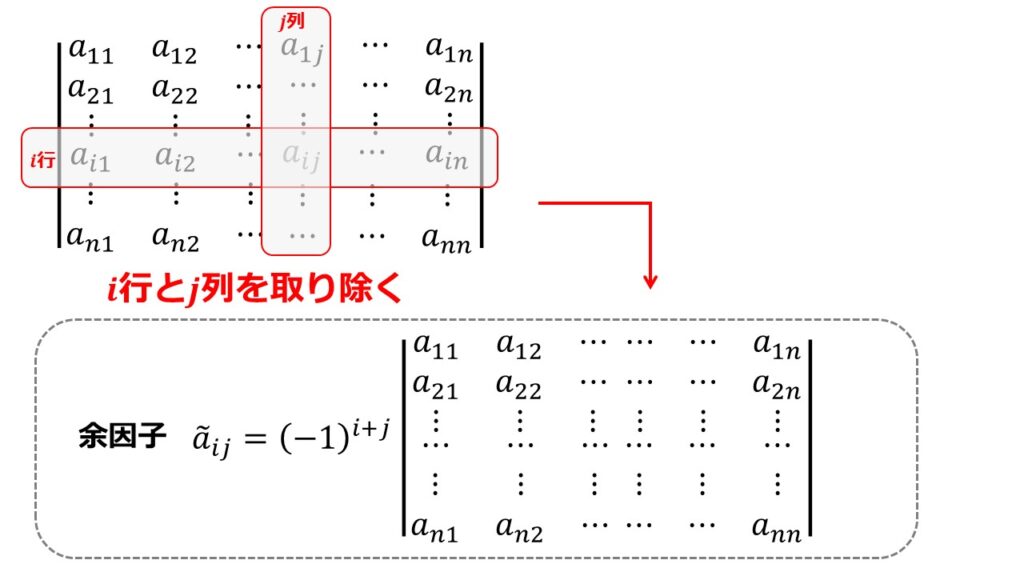
余因子行列を定義
この余因子を使って余因子行列を以下のように定義します。
\tilde{A}=\underset{転置行列であることに注意}{{}^t\!\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{12} &\cdots &\tilde{a}_{1n} \\
\tilde{a}_{21} &\tilde{a}_{22} &\cdots &\tilde{a}_{2n} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{n1} &\tilde{a}_{n2} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}}\\
=\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{21} &\cdots &\tilde{a}_{n1} \\
\tilde{a}_{12} &\tilde{a}_{22} &\cdots &\tilde{a}_{n2} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{1n} &\tilde{a}_{2n} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}
\end{align*}
行列の要素がすべて余因子であることと、余因子行列は転置行列であることに注意しましょう。
余因子行列を使うと逆行列が求まる
では正方行列$A$と先ほど定義した余因子行列$\tilde{A}$の掛け算を計算してみましょう。
A\tilde{A}=\begin{pmatrix}
a_{11} &a_{12} &\cdots &a_{1n} \\
a_{21} &a_{22} &\cdots &a_{2n} \\
\cdots &\cdots&\cdots &\cdots \\
a_{n1} &a_{n2} &\cdots &a_{nn} \\
\end{pmatrix}\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{21} &\cdots &\tilde{a}_{n1} \\
\tilde{a}_{12} &\tilde{a}_{22} &\cdots &\tilde{a}_{n2} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{1n} &\tilde{a}_{2n} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}\\
=\begin{pmatrix}
a_{11}\tilde{a}_{11}+a_{12}\tilde{a}_{12}+\cdots +a_{1n}\tilde{a}_{n1} &\cdots &\cdots \\
a_{21}\tilde{a}_{11}+a_{22}\tilde{a}_{12}+\cdots +a_{2n}\tilde{a}_{n2}&\cdots &\cdots \\ \\
\cdots &\cdots&\cdots \\
a_{n1}\tilde{a}_{11}+a_{n2}\tilde{a}_{12}+\cdots +a_{nn}\tilde{a}_{nn} &\cdots &\cdots
\end{pmatrix}
\end{align*}
行列の掛け算をした結果は$n$行$n$列になっています。
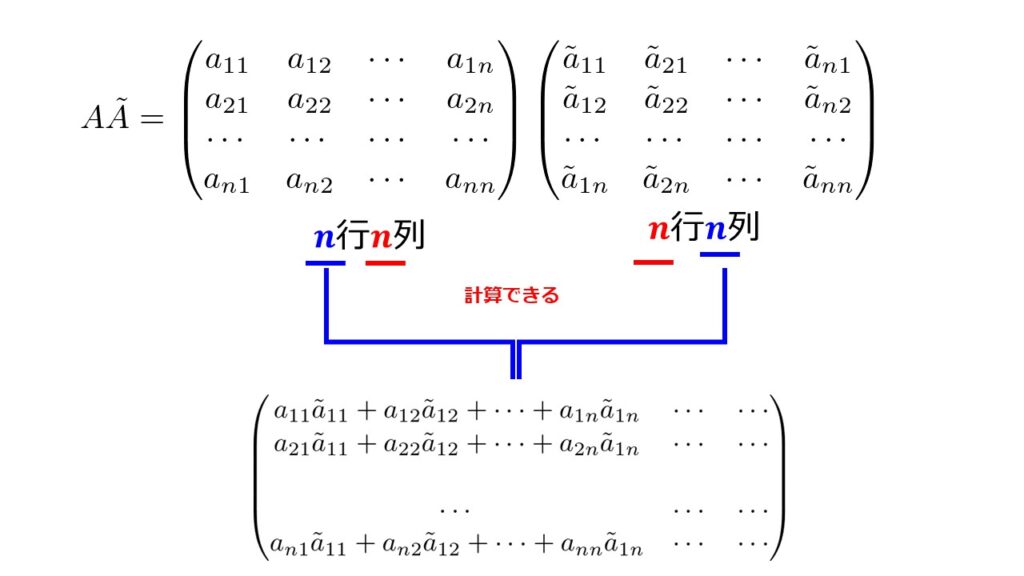
どうなっているのかを対角成分と非対角成分でわけて考えてみましょう。
■(1,1)成分について
a_{11}\tilde{a}_{11}+a_{12}\tilde{a}_{12}+\cdots +a_{1n}\tilde{a}_{1n}=|A|
\end{align*}
これは1行目に関する余因子展開になっているのがおわかりいただけただろうか。
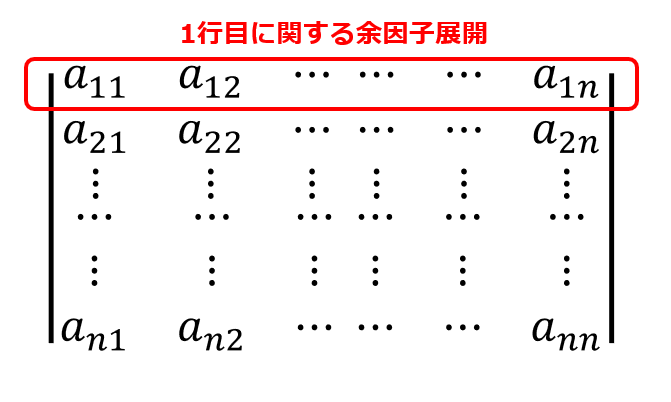

よって結果は行列式$|A|$になります。
後で示すように、このように対角成分は全て$|A|$になります。
■(1,2)成分について
a_{21}\tilde{a}_{11}+a_{22}\tilde{a}_{12}+\cdots +a_{2n}\tilde{a}_{1n}=0
\end{align*}
結果は0になります。
なぜかと言うと1行目に関する余因子展開ではありますが、1行目と2行目が同じである場合の余因子展開をしていることになるからです。
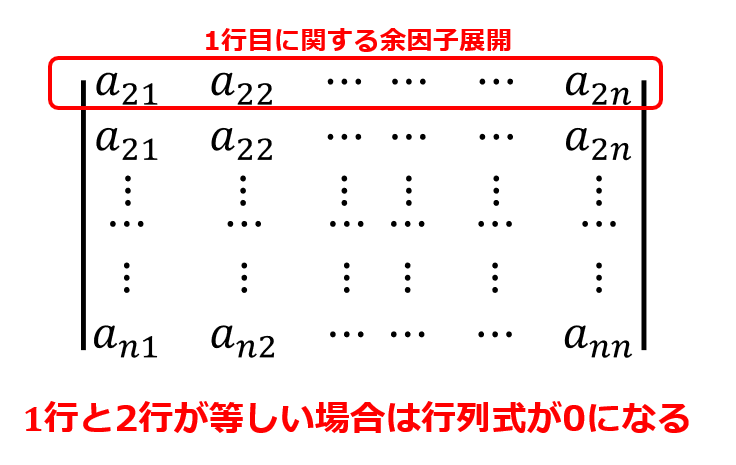

前回の記事でも解説したように等しい行がある場合の行列式の結果は0になるため、(1,2)成分の結果は0になったというわけです。
対角成分は行列式$|A|$になり、非対角成分は0になります。
以上をまとめると、$A\tilde{A}$の$(i,j)$成分はクロネッカー$\delta_{ij}$を使うと以下のように書くことができます。
a_{i1}\tilde{a}_{1j}+a_{i2}\tilde{a}_{1j}+\cdots +a_{in}\tilde{a}_{nj}=\delta_{ij}|A|
\end{align*}


結局どうなるのかと言うとこうなります。
A\tilde{A}&=\begin{pmatrix}
a_{11} &\cdots &a_{1j}&\cdots &a_{1n} \\
\cdots &\cdots&\cdots &\cdots &\cdots \\
a_{i1} &\cdots &a_{ij}&\cdots &a_{in} \\
\cdots &\cdots&\cdots &\cdots &\cdots \\
a_{n1} &\cdots &a_{n2}&\cdots &a_{nn} \\
\end{pmatrix}\begin{pmatrix}
\tilde{a}_{11} &\cdots &\tilde{a}_{j1} &\cdots &\tilde{a}_{n1} \\
\cdots &\cdots&\cdots &\cdots &\cdots \\
\tilde{a}_{1i} &\cdots &\tilde{a}_{ji} &\cdots &\tilde{a}_{ni} \\
\cdots &\cdots&\cdots &\cdots &\cdots \\
\tilde{a}_{1n}&\cdots &\tilde{a}_{jn}&\cdots &\tilde{a}_{nn} \\
\end{pmatrix}\\
&=\begin{pmatrix}
|A| & 0 &0&\cdots &0 \\
0 & |A| &0&\cdots &0 \\
\cdots &\cdots&\cdots &\cdots &\cdots \\
0 & 0 &0&|A| &0 \\
0 & 0 &0&\cdots &|A| \\
\end{pmatrix}\\
&=|A|\begin{pmatrix}
1& 0 &0&\cdots &0 \\
0 & 1 &0&\cdots &0 \\
\cdots &\cdots&\cdots &\cdots &\cdots \\
0 & 0 &0&1 &0 \\
0 & 0 &0&\cdots&1
\end{pmatrix}\\
&=|A|\underset{単位行列}{E}
\end{align*}
対角成分が行列式$|A|$で共通なので外に出すと単位行列になります。
よって、
A\,\frac{1}{|A|}\tilde{A}=E
\end{align*}
となるわけです。
ここでもう一度逆行列の定義をおさらいしましょう。
$n$次正方行列$A$に対して$XA=AX=E$($E$は単位行列)となる行列$X$が存在するとき、$X$を$A$の逆行列と言い、$X=A^{-1}$と表します。
※行列には割り算の記法がないため$\frac{1}{A}$とは書きません。
まさに$\frac{1}{|A|}\tilde{A}$がその逆行列の部分になっていますね。
逆行列は余因子行列$\tilde{A}$を用いて具体的に書くと、
\frac{1}{|A|}\tilde{A}&=\underset{転置行列であることに注意}{{}^t\!\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{12} &\cdots &\tilde{a}_{1n} \\
\tilde{a}_{21} &\tilde{a}_{22} &\cdots &\tilde{a}_{2n} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{n1} &\tilde{a}_{n2} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}}\\
&=\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{21} &\cdots &\tilde{a}_{n1} \\
\tilde{a}_{12} &\tilde{a}_{22} &\cdots &\tilde{a}_{n2} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{1n} &\tilde{a}_{2n} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}
\end{align*}
となります。
よって逆行列$A^{-1}$は、
と書けるというわけです。
行列式の導出をする機会はあまりないですが「行列の掛け算」「余因子展開」「余因子行列」の復習にもなるので手を動かして導出してみましょう(^^)/
まとめ
$n$次正方行列$A$に対して$XA=AX=E$($E$は単位行列)となる行列$X$が存在するとき、$X$を$A$の逆行列と言い、$X=A^{-1}$と表します。
※行列には割り算の記法がないため$\frac{1}{A}$とは書きません。
余因子行列$\tilde{A}$は逆行列を計算する際に必要ですのでおさえておきましょう!
\tilde{A}=\underset{転置行列であることに注意}{{}^t\!\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{12} &\cdots &\tilde{a}_{1n} \\
\tilde{a}_{21} &\tilde{a}_{22} &\cdots &\tilde{a}_{2n} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{n1} &\tilde{a}_{n2} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}}\\
=\begin{pmatrix}
\tilde{a}_{11} &\tilde{a}_{21} &\cdots &\tilde{a}_{n1} \\
\tilde{a}_{12} &\tilde{a}_{22} &\cdots &\tilde{a}_{n2} \\
\cdots &\cdots&\cdots &\cdots \\
\tilde{a}_{1n} &\tilde{a}_{2n} &\cdots &\tilde{a}_{nn} \\
\end{pmatrix}
\end{align*}
逆行列$A^{-1}$は、
と書けます。
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/