前回の記事で「1次元のオイラーの運動方程式(非粘性)」からベルヌーイの定理を導きました。
ベルヌーイの定理は、以下のように記述できます。
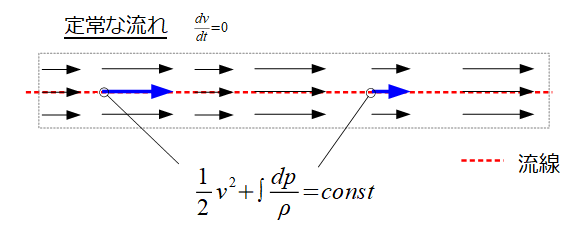
赤点線の流線に沿って成り立つエネルギー保存則を意味しています。
\frac{1}{2}v^2+\int \frac{dp}{\rho}=const\cdot\cdot\cdot (1)
\end{align*}
できればこれを具体的な形で計算をしたい場のですが、どうすればよいでしょうか?
もちろん(1)式の積分を実行することを考えるはずですね。
つまり、密度\(\rho\)と圧力\(p\)との関係式がわかれば良いと言う事になりますが、そんな津ぐうの良いものがあるのでしょうか?
その時にバロトロピー流れというのを考えます。
何も難しく考えずに、バロトロピー流れとは、密度が圧力のみの関数として場合にそのように呼んでいるだけです。
このように書くと、密度は圧力の関数でありますし、逆に圧力は密度の関数でもありますので(1)式の積分を実行することができます。
そこで、この記事ではどのような状況下(限定的?)でバロトロピー流れというのを考えることができるのかをまとめたいと思います。
熱力学における状態量
熱力学的な状態を定めるのに、どのような状態変数を定めれば良いかというのがあります。
「圧力?」「温度?」「体積?」「内部エネルギー?」「エントロピー?」「エンタルピー?」などなど・・・・・
これらは独立なのではなく、互いに関係性をもった状態量になります。
熱力学ではこのうちの2つの独立変数を定めれば熱力学的な状態というのが定まります。
「熱力学的な状態が定まる」とは、どのような平衡状態かがわかるという意味です。
もう少し具体的に言うと、「どのような平衡状態か」がわかればそのときのマクロ変数である、圧力、温度、体積、内部エネルギー、エントロピー、エンタルピーなどもが芋づる式に決定されていきます。
上記で言っていることがよくわからない場合は、1つの例として理想気体の状態方程式、
pV=nRT\cdot\cdot\cdot (3)
\end{align*}
を考えましょう。
これを下記のようにします。
p=\rho {R}’ T\cdot\cdot\cdot (4)
\end{align*}
※\({R}’=\frac{R}{MW}\)
※\(MW\):モル質量
そうすると、変数は圧力\(p\)、密度\(\rho\)、温度\(T\)の3つです。
式は1つなので、自由度は3-1=2になります。
状態を決定するためには、3つのうち2つの変数を決定すれば良いというのが理解できるかと思います。
その状態方程式を一般的に書くのであれば、
f(p,\rho,T)=0\cdot\cdot\cdot (5)
\end{align*}
または、
f(p,V,T)=0\cdot\cdot\cdot (6)
\end{align*}
となります。
以下の記事にも詳しく書いていますのでご参考ください。
ならば変数を何に選ぶかは、「考えやすい変数を選ぶ」という理由の元で好きなものを選べば良いということになります。
↓下記の熱力学的な変数のうち、どの2つを変数に選ぶかは状況次第です。
\(p\):圧力
\(T\):温度
\(V\):体積
\(U\):内部エネルギー
\(S\):エントロピー
\(H\):エンタルピー
※赤色:示強変数、青色:示量変数
密度\(\rho\)の変数をエントロピー\(s\)と\(p\)と選ぶ
理解しやすい変数を2つ選ぶとすると、密度\(\rho\)の変数をエントロピー\(s\)と\(p\)と選ぶことにします。
※小文字で\(s\)書くと単位体積あたりのエントロピーを考えているっぽいですが、まさにそう考えているので小文字で書いています。(今回の話にはあまり本質ではありませんが)
しかし、圧力を小文字で書いているのは大文字で書くのが面倒だからで決して「単位体積あたりの圧力」と解釈してはいけません。
エントロピーは示量変数であるので、エントロピー密度なるものが定義できますが(部分系のエントロピーに体積をかけると、全体系のエントロピーになる(\(S=Vs\)))、圧力は示強変数なので部分系の圧力と全体系の圧力は等しいです。
では密度を、エントロピー\(s\)と圧力\(p\)を用いて
\rho=\rho (s,p)\cdot\cdot\cdot (7)
\end{align*}
と書くことにします。
等エントロピー流れのとき
等エントロピー流れとは、流れに沿って流体粒子が運動するときにエネルギーが逃げたり加えられたりしない状況のことを言います。
つまり、断熱変化のことです。
そうすると、エントロピーは変化しないので、
ds=0\cdot\cdot\cdot (8)
\end{align*}
となります。
補足説明ですが、エントロピーは平衡状態であれば\(S\)として定義できます。
そのとき、熱量変化\(dQ\)とエントロピーの関係式は、温度\(T\)を用いて、
dQ=TdS\cdot\cdot\cdot (9)
\end{align*}
と書けるので、断熱変化\(dQ=0\)ならば、等エントロピー流れ\(dS=0\)となります。
※単位体積あたりとして、\(dq=Tds\)として理解してもよいです。
そうすると密度\(\rho=\rho (s,p)\)でありましたがエントロピーの\(s\)は変数でなくなるので密度は、
\rho=\rho (p)\cdot\cdot\cdot (10)
\end{align*}
となり、バロトロピー流れになります。
この場合の理想気体であれば(10)式の具体的な形は、
\frac{p}{\rho^{\gamma}}=const
\end{align*}
です。
※\(\gamma\):比熱比
これは、熱力学第一法則と理想気体の状態方程式から導出することができます。
等温過程の場合
等温過程の場合はどうでしょうか。
等温過程とは、字のごとく「平衡状態から別の平衡状態へ行く過程で温度が変わらない」という意味です。
状態方程式\(f(p,\rho,T)=0\)を考えるに、等温過程では温度が変数ではなくなるので、
f(p,\rho)=0\cdot\cdot\cdot (11)
\end{align*}
となり、圧力\(p\)と密度\(\rho\)の関係式になりました。
これだけでは\(\rho\)が\(p\)の関数かどうかは知りませんが・・・・圧力\(p\)によって密度\(\rho\)が2つ以上決まるなんて物理的に不思議なことが起こらないと考えれば、(11)式より密度\(\rho\)は圧力\(p\)の関数となっているでしょう。
よって、等温過程でも
\rho=\rho (p)\cdot\cdot\cdot (12)
\end{align*}
となり、バロトロピー流れとして考えることができます。
この場合、理想気体ならば(12)式の具体的な形は、
\frac{p}{\rho}=const
\end{align*}
です。
理想気体の状態方程式\(p=\rho {R}’ T\)で温度を一定と考えれば理解できるでしょう。
密度が一定の場合
非圧縮性の流体として取り扱う場合は、密度変化が小さいとして密度を一定にすることがありますが、バロトロピー流れとの関係はどうでしょうか。
\rho=\rho (p)
\end{align*}
のように密度が圧力の関数になっているのがバロトロピー流れでしたが、密度が一定、すなわち何にも依存していない定数なら、この場合もよりバロトロピー流れの一部であると言えるでしょう。
よって密度一定の場合も、バロトロピー流れの一部です。
この時の具体的な密度は、具体的も何もないですが、
\rho=const
\end{align*}
となります。密度は物性値を当てはめることになります。
※余談ですが、
\frac{1}{2}v^2+\int \frac{dp}{\rho}=const\cdot\cdot\cdot (1)
\end{align*}
より、密度を一定にすると積分の外に密度を出すことができますので、積分を実行すると、
\frac{1}{2}v^2+\frac{p}{\rho}=const\cdot\cdot\cdot (13)
\end{align*}
となります。
これが、非圧縮性の流体でのベルヌーイの定理になります。
まとめ
多くの流体現象においては上記の状況下であることが多いですが、例えば水が水蒸気になるような気化熱を伴う現象の場合にバロトロピー流れとして扱えない場合があるので、そういったことに十分留意してください。