こんにちは(@t_kun_kamakiri)(^^)/
本記事では、直交関数系についてのお話をします(^^)/
数学的な厳密性はひとまず置いておくとして、イメージで説明していき、理解できればと思います。
関数の集合\(\left \{f_{0}(x), f_{1}(x)\cdot\cdot\cdot,f_{n}(x)\right \}\)が以下を満たすとして、
\int ^{\infty}_{-\infty}f_{i}(x)f_{j}(x)dx=\left\{\begin{matrix}
1\left ( i=j \right )\\0\left ( i\neq j \right )
\end{matrix}\right.
\end{align*}
これらの関数の集合を用いて任意の関数\(f(x)\)は、
と書けるというお話です。
この記事では、
- 関数の直交性
- 直交関数系を使って任意の関数を書ける理由
これを高校生で習った直交する単位ベクトルを使えば任意のベクトルを書くことができる(下図)というわりと簡単なところから理解できればと思っています(^O^)
まずは関数の直交性について話していきます!
関数の直交性
関数の集合\(\left \{ f_{0}(x),f_{1}(x)\cdot\cdot\cdot,f_{n}(x),\cdot\cdot\cdot\right \}\)があるとします。
その中から任意の異なる関数を取り出して掛け算して積分すると0になる関数の集合のことを関数直交関数系といいます。
こういうふうに言葉にすると難しいですが、数式でかいてあげます。
例えば、関数の集合の中から異なる関数を2つ選んで掛け算して積分します(^^)
\int^{\infty}_{-\infty}f_{0}(x)f_{1}(x)dx=0
\end{align*}
\int^{\infty}_{-\infty}f_{1}(x)f_{2}(x)dx=0
\end{align*}
・
・
・
\int^{\infty}_{-\infty}f_{i}(x)f_{j}(x)dx=0\tag{1}
\end{align*}
※\(i\neq j\)
・
・
・
異なる関数同士ならこのように掛け算して積分すると0になる関数系のことを関数の直交性といいます。
※積分区間は無限大にしなくても、有限の区間にしておいても良いです。
では、同じ関数系\(f_{i}(x)\)どうしなら、
これらをまとめて、
\int^{\infty} _{-\infty}f_{i}(x)f_{j}(x)dx=\left\{\begin{matrix}
1\left ( i=j \right )\\0\left ( i\neq j \right )
\end{matrix}\right.\tag{3}
\end{align*}
(3)式を満たすような関数の集合\(\left \{f_{0}(x),f_{1}(x)\cdot\cdot\cdot,f_{n}(x)\right \}\)を正規直交関数系といいます。
- (1)式が関数の直交性
- (2)式が正規(1という意味)
次に、「(3)式の何がうれしいのか?」というお話をします(^^)/
正規直交関数系を使って任意の関数を作ることができる
章のタイトル通り、(3)式を満たす関数の集合(正規直交関数系)を用いると任意の関数を作ることができるというのが嬉しいことです。
線形代数にも、正規直交ベクトルを用いると任意のベクトルを作ることができるというやつがあったのを思い出します。
この記事によると・・・
線形空間とか元とかよくわからない用語はさておき、次元を減らして2次元のベクトルで考えると、こういうことです。


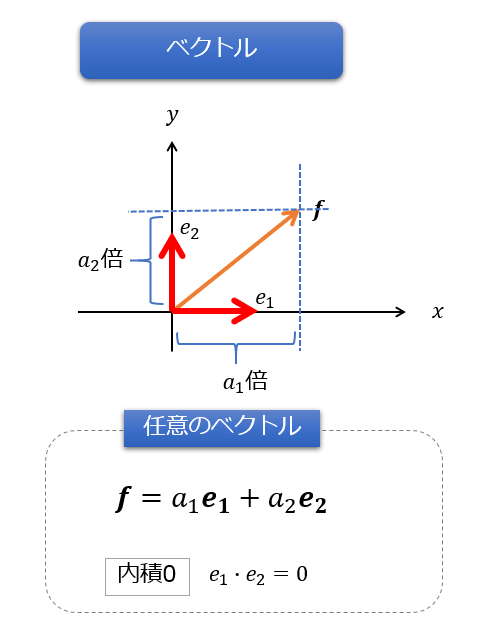
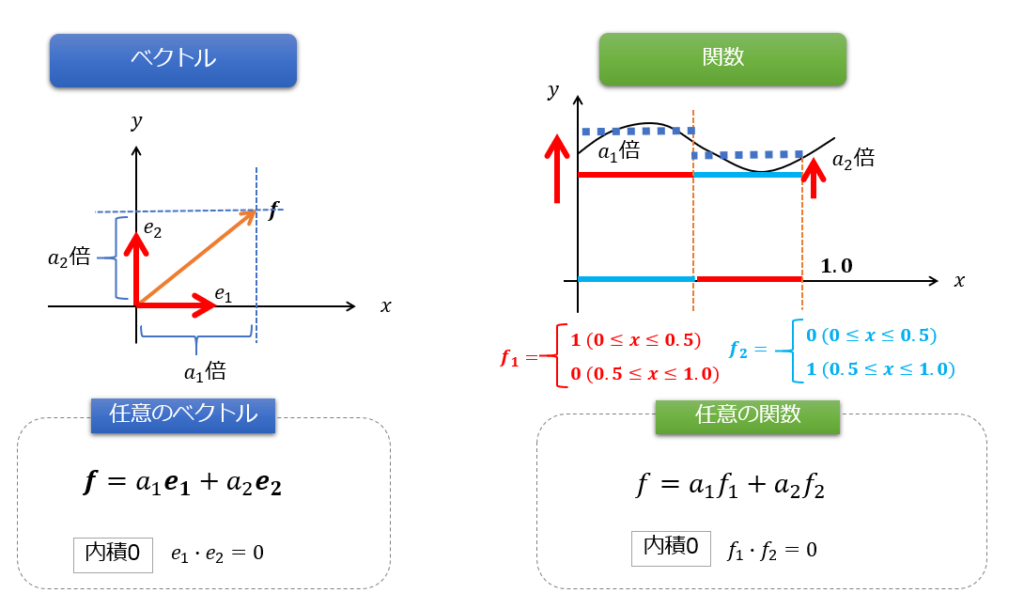
任意のベクトル\(\boldsymbol{f}\)は、互いに直交なベクトル\(\boldsymbol{e}_{1}\)と\(\boldsymbol{e}_{2}\)の線形結合で記述できます。
3次元の場合は、任意のベクトルは\(\boldsymbol{f}=a_{1}\boldsymbol{e}_{1}+a_{2}\boldsymbol{e}_{2}+a_{3}\boldsymbol{e}_{3}\)となるという話です。
それを\(n\)次元まで考えて一般化すると上のような記述になるというわけです(^^)/
これは高校生でもよく使っているので馴染みがあるかと思います。
※同じベクトル同士の内積が1であるものを選ぶ必要はなく、便宜上1になってくれた方が計算がしやすいだけの理由です。
この考え方を応用して、直交関数系を用いると任意の関数を書けることについて考えていきたいと思います。
直交関数系を使って任意の関数を書ける理由
ベクトル同様に、関数についても直交性のある関数の集合を用いると任意の関数を書けるという理由を考えていきたいと思います。
関数の集合:\(\left \{f_{0}(x),f_{1}(x)\cdot\cdot\cdot,f_{n}(x)\right \}\)
任意の関数\(f(x)\)
関数を2分割してみる
簡単に考えるために、以下のような形の関数を考えます。
※範囲は[\(0\leq x \leq 1\)]とします。
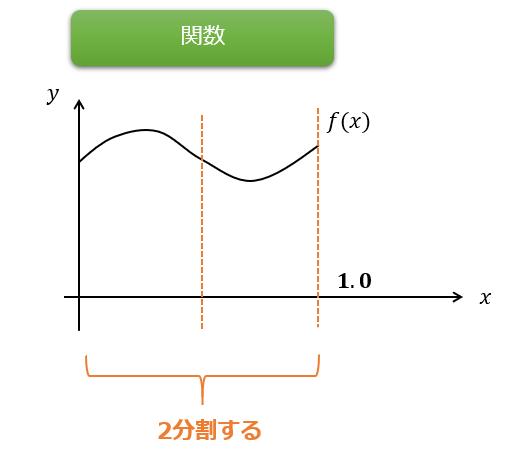

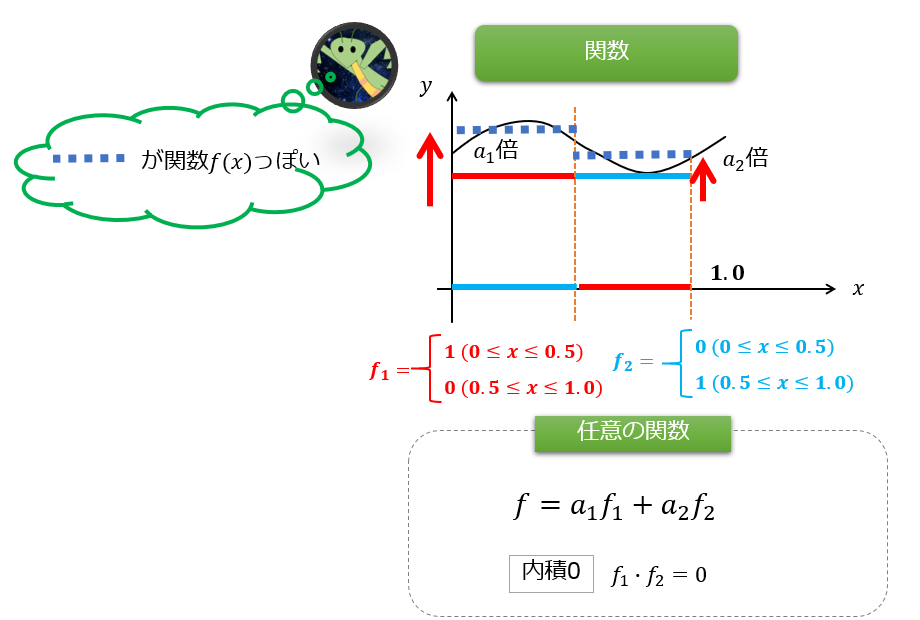
この関数を関数の集合\(f_{1}(x),f_{2}(x)\)で書くことを考えます。
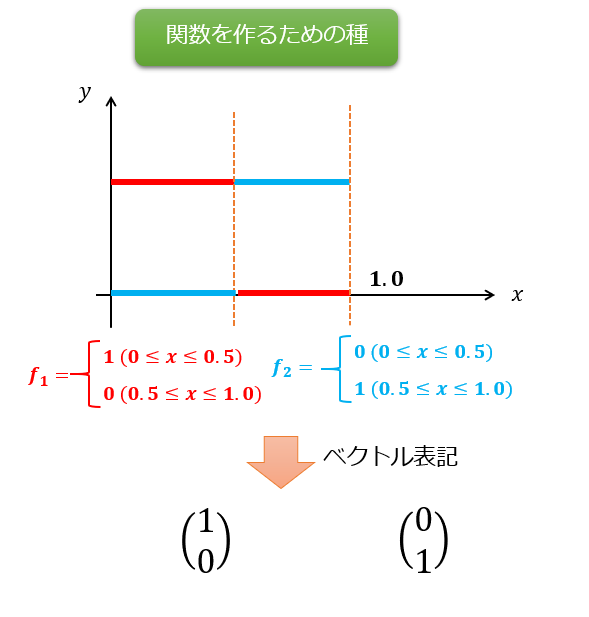

このような関数を用意します。
当然これは、\(f_{1}\cdot f_{2}=0\)の直交性を満たしています。
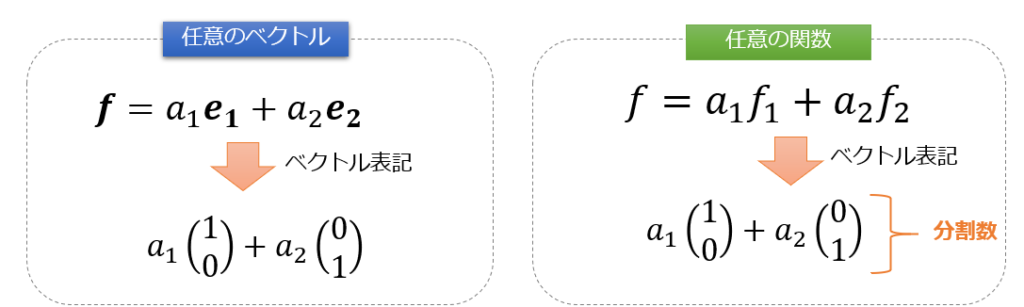
ベクトルとの類似性をわかりやすくるためにベクトルの表記にして書いてみました(‘ω’)
この関数を関数の集合\(f_{1},f_{2}\)を使って、任意の関数\(f(x)\)を書こうとすると、以下のように関数の集合\(f_{1},f_{2}\)を使って線形結合すれば良いことがわかります。

全然分割数が足りませんでした(笑)
が、ベクトルの場合と関数の場合でとても似ているということが理解できたかと思います。


関数を\(n\)分割数にしてみる
先ほどのような関数を2分割した程度では全然関数の滑らかな感じにはならなかったので、とりあえず\(n\)分割してみます。
(\(n\)はとりあえず・・・・1000分割くらいで考えます( ^ω^)・・・)
関数\(f(x)\)の範囲は、[\(0\leq x \leq L\)]としておきます。
関数\(f(x)\)を作るための種である関数の集合\({f_{1}(x),f_{2}(x),\cdot\cdot\cdot,f_{n}(x)}\)を用意します。
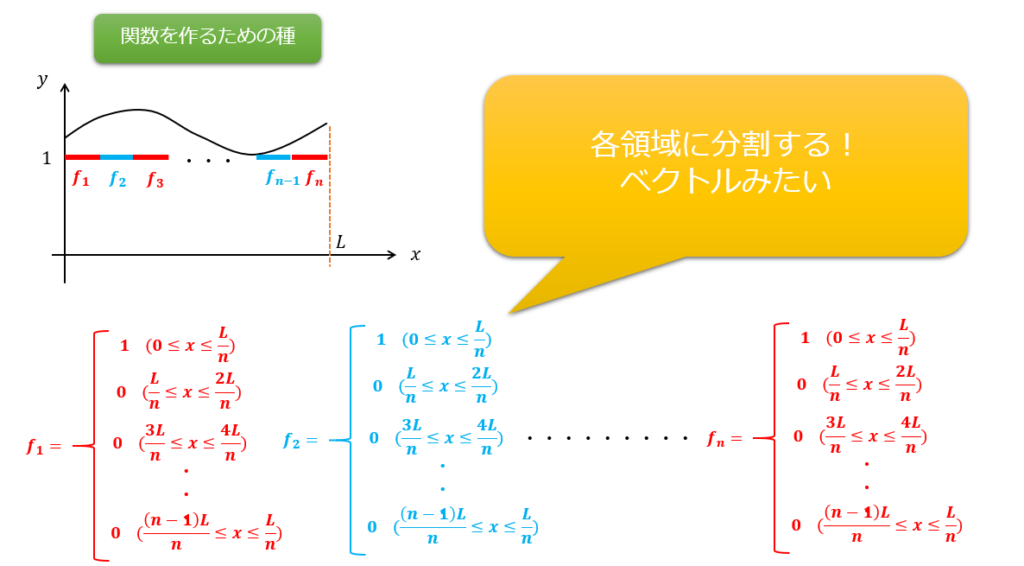

では、先ほどと同様に関数の集合\(f_{1}(x),f_{2}(x),\cdot\cdot\cdot,f_{n}(x)\)を使って任意関数\(f(x)\)を作ります。
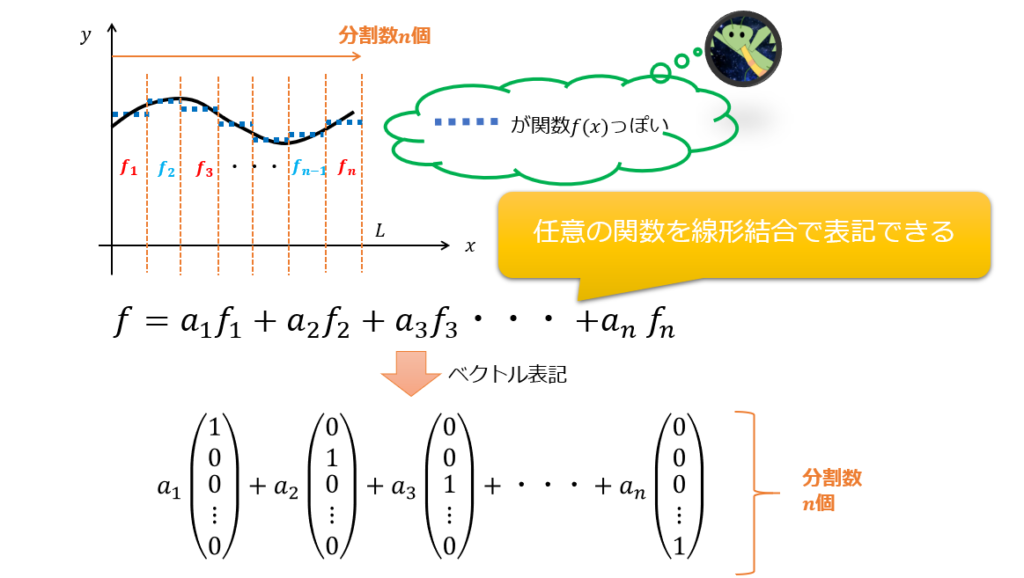

これも、関数の集合{\(f_{1}(x),f_{2}(x),\cdot\cdot\cdot,f_{n}(x)\)}をベクトル表記で書いたとすると、直交性
f_{i}\cdot f_{j}=0\tag{5}
\end{align*}
を満たしています。
この関数の集合{\(f_{1}(x),f_{2}(x),\cdot\cdot\cdot,f_{n}(x)\)}の直交性を絵で書いてみます。
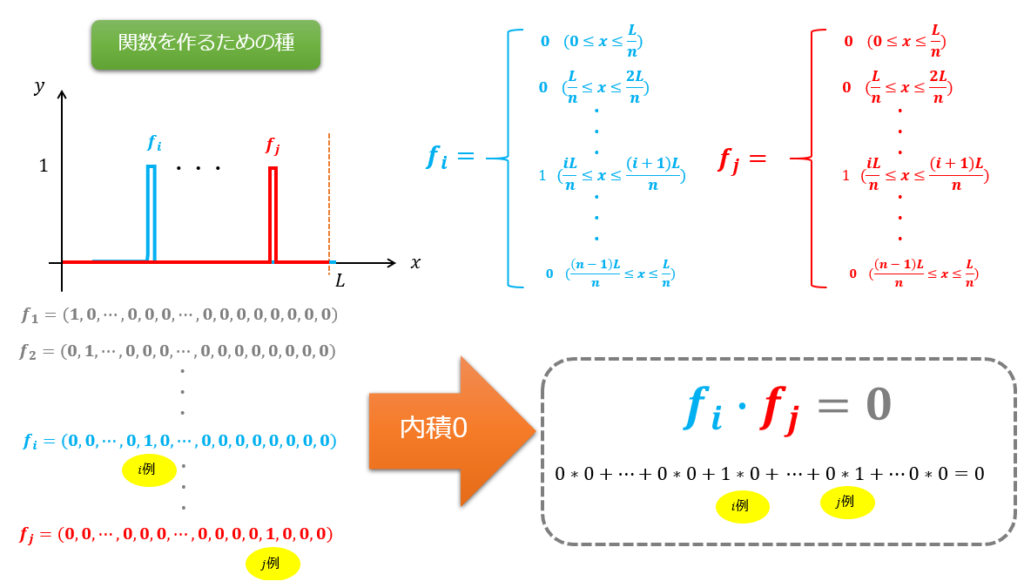

グラフとベクトルの各成分の値とがリンクしやすいように、ベクトルを列ベクトルで書きました。
今、\(f_{i}(x)\)は関数なのですが、わかりやすくるためにベクトルで表現しています。
異なるベクトル同士の内積(\(f_{i}(x)\cdot f_{j}(x)\))はやはり\(0\)です。
関数を\(\infty\)分割数にしてみる
\(n\)分割した関数の集合集合{\(f_{1}(x),f_{2}(x),\cdot\cdot\cdot,f_{n}(x)\)}を使って、分割数を\(\infty\)個にしてみます。
\(n\)分割の場合は、\(f_{i}\)の幅は\(\frac{L}{n}\)であったのですが、その幅を無限小まで小さくすることを考えます。
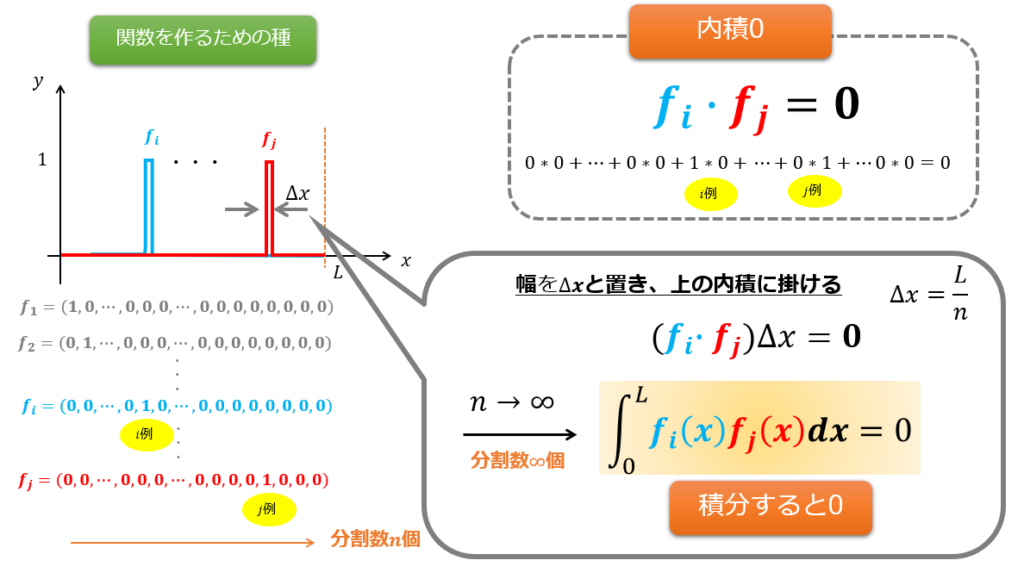

これにより、関数の直交性とは異なる関数\(f_{i}(x),f_{j}(x)\)の掛け算を区間で積分した値が0、つまり、
\int^{L}_{0}f_{i}(x)f_{j}(x)=0\tag{6}
\end{align*}
ということになります。
今の場合は、同じ関数\(f_{i}\)同士の掛け算を区間で積分した値は\(1\)になるので、そのことを(6)式とまとめると、
\int^{L}_{0}f_{i}(x)f_{j}(x)=\delta_{ij}\tag{7}
\end{align*}
ただし、\(\delta_{ij}\)はクロネッカーデルタです。
\delta_{ij}=\left\{\begin{matrix}
1 (i=j) \\0 (i\neq j)
\end{matrix}\right.
\end{align*}
まとめ
数学的な厳密性はあまり考えずに感覚的に理解しようと試みました(^^)/
以下が本記事のまとめです。
という知見をお借りすると・・・
これらの関数の集合\(\left \{f_{0}(x), f_{1}(x)\cdot\cdot\cdot,f_{n}(x)\right \}\)を用いて任意の関数\(f(x)\)は、
と書けます(^^)/