こんにちは(@t_kun_kamakiri)(^^)/
前回では、「行列の計算方法」についての記事をまとめました。
今回は転置行列について解説を行います。
- 転置行列の定義
- 積の転置行列\({}^t\!(AB)={}^t\!B\,{}^t\!A{}\)の証明
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事を読むと転置行列についてよくわかることでしょう!
転置行列の定義
$(m,n)$型行列$A$の縦横を逆にした$(n,m)$行列を$A$の転置行列と言います。
$A$の転置行列\({}^t\!A\)と書きます。
※転置行列を$A^{T}$と表記することもあります。
具体的に$(m,n)$型行列$A$の転置行列を書いてみましょう。
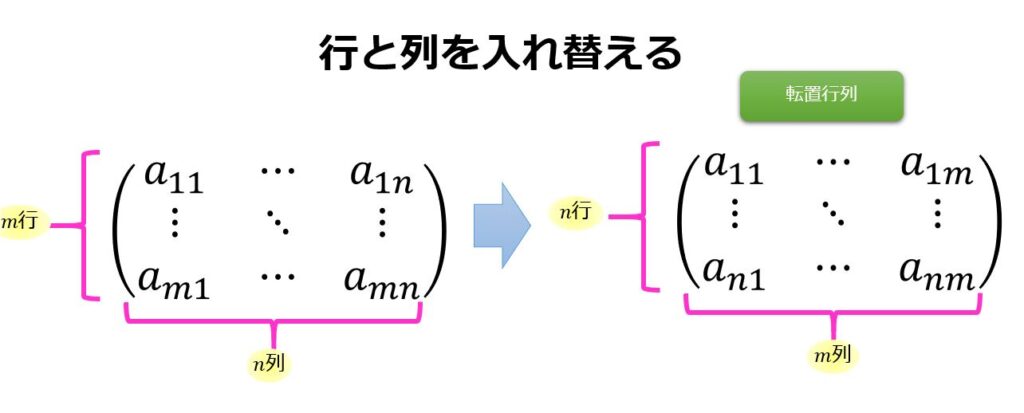

一般的すぎるとわかりにくいですね・・・
行列$A$を3行2列の行列とします。
$A=\begin{pmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}\\
a_{31} & a_{32}\\
\end{pmatrix}$を用意して、この行列$A$の転置行列(行と列を入れ替える)は、
\({}^t\!A=\begin{pmatrix}
a_{11} & a_{21} & a_{31}\\
a_{12} & a_{22} & a_{32}\\
\end{pmatrix}\)となり、2行3列の行列になります。
このように行列$A$の$(i,j)$成分の値は$a_{ij}$ですが、転置行列\({}^t\!A\)の$(i,j)$成分の値は$a_{ji}$となっています。
具体的に言うと$A$の$(1,2)$成分の値は$a_{12}$ですが、転置行列\({}^t\!A\)の$(1,2)$成分の値は$a_{21}$となっているということです。
成分の添え字が入れ替わっていることに注意しましょう。


行と列を入れ替えたので、成分の添え字が入れ替わっているということですね。
行列$A$を4行3列の行列とします。
$A=\begin{pmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
10 & 11 & 12\\
\end{pmatrix}$
この行列$A$の転置行列(行と列を入れ替える)を考えてみましょう。
簡単ですね。
行と列を入れ替えればよいので、
\({}^t\!A=\begin{pmatrix}
1 & 4 & 7 & 10\\
2 & 5 & 8 & 11\\
3 & 6 & 9 & 12\\
\end{pmatrix}\)となり、3行4列の行列になります。
転置行列は行と列を入れ替えた行列だということが理解できたことでしょう(^^)
積の転置は積の左右を入れ替えた転置の積を与える
では、転置行列で重要な基本法則をいくつか紹介します。
この中で一番曲者は\({}^t\!(AB)={}^t\!B\,{}^t\!A{}\)でしょう。
ということで、今回は\({}^t\!(AB)={}^t\!B\,{}^t\!A{}\)の証明をして本記事を終えたいと思います。
\({}^t\!(AB)={}^t\!B\,{}^t\!A{}\)の証明
$(l,m)$型の行列$A$と、$(m,n)$型の行列$B$を考えます。
このとき行列の積$AB$の$(i,j)$成分は以下のように書けます。
(AB)_{ij}&=\sum^{m}_{k=1}a_{ik}b_{kj}\\
&=a_{i1}b_{1j}+a_{i2}b_{2j}\cdots +a_{im}b_{mj}
\end{align*}
となります。
$m$の数が同じなので行列の掛け算が行えますね。
こちらは前回の記事(行列の計算)でも解説を行いましたので怪しい方は↓こちらの記事をご参考ください。
では、\({}^t\!(AB)\)の成分だけを考えて計算を進めてみましょう。
{}^t\!(AB)_{ij}&=\sum^{m}_{k=1}{}^t\!(a_{ik}b_{kj})\\
&\underset{iとj\\を入れ\\替え}{=}\sum^{m}_{k=1}a_{jk}b_{ki}\\
&=\sum^{m}_{k=1}b_{ki}a_{jk}\\
&=\sum^{m}_{k=1}{}^t\!b_{ik}{}^t\!a_{kj}\\
&=({}^t\!B\,{}^t\!A)_{ij}
\end{align*}
よって、
となります。
※行列の積は入れ替えに対して$AB\neq BA$なので安易に行列の積を入れ替えてはいけなません。
{}^t\!(AB)\underset{これは間違い}{=}{}^t\!A\,{}^t\!B
\end{align*}
まとめ
$(m,n)$型行列$A$の縦横を逆にした$(n,m)$行列を$A$の転置行列と言い、$A$の転置行列\({}^t\!A\)と書きます。
簡単に言うと転置行列とは行と列を入れ替えた行列のことです。
転置行列の基本的な性質は以下となります。
特に4番目の\({}^t\!(AB)={}^t\!B\,{}^t\!A{}\)は必ず覚えておきましょう!
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/