【行列式の計算（サラスの公式）】3次正方行列は簡単。

こんにちは(@t_kun_kamakiri)(^^)/

前回では、「なぜ行列式の計算するのか？」という内容で記事をまとめました。

前回の記事

【なぜ行列式の計算するのか？】大学一年生にも超わかりやすく解説する。

前回の記事で「なぜ行列式を計算するのか？」という問いに対しては「逆行列の有無の判断に使えるから」であるということを書きました。

今回は行列式について解説を行います。

本記事の内容

2次正方行列
3次正方行列の行列式はサラスの公式を使う

※4次以上の正方行列に対する行列式の計算方法は次回の記事で解説を行います。

これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。

こんな人が対象

行列をはじめて習う高校生・大学生
仕事で行列を使うけど忘れてしまった社会人

この記事を読むと3次正方行列が簡単に求めることができるようになります(^^)/

行列式の具体的な計算
1. 2次正方行列
2. 3次正方行列（サラスの公式）
まとめ
参考にする参考書はこれ

行列式の具体的な計算

行列式の具体的な計算方法を解説します。

以下の正方行列に対して行列式を考えてみましょう。

2次の正方行列
2行2列の行列ですね。

$A=\begin{pmatrix}
a &b\\
c & d\tag{2}
\end{pmatrix}\\$

3次の正方行列
3行3列の行列ですね。

$A=\begin{pmatrix}
a_{11} &a_{12} & a_{13} \\
a_{21} &a_{22} & a_{23} \\
a_{31} &a_{32} & a_{33} \tag{3}
\end{pmatrix}\\$

本記事では3次の正方行列に対する行列式までを扱います。

※4次以上の正方行列に対する行列式については少々難しくなるので別の記事で解説を行います。

4次の正方行列
※4次以上の正方行列の行列式はちょっと複雑になります。

$A=\begin{pmatrix}
a_{11} &a_{12} & a_{13} \\
a_{21} &a_{22} & a_{23} \\
a_{31} &a_{32} & a_{33} \\
a_{41} &a_{42} & a_{43} \tag{4}
\end{pmatrix}\\$

なぜ正方行列に対する行列式しか考えないのかについて後で書いておきます。
※結論を先に言っておくと正方行列ではない行列（例えば2行3列の行列）は行列式が計算できません。したがって逆行列も存在しないことになります。

2次正方行列

2次の正方行列$A=\begin{pmatrix}
a &b\\
c & d
\end{pmatrix}$の行列式を考えましょう。

2次の正方行列の行列式はとても簡単です。

対角線同士の掛け算を行い、各々の掛け算の結果で引き算を行います。

\begin{align*}
|A|&=\begin{vmatrix}
a &b\\
c & d
\end{vmatrix}=ad-bc\tag{5}
\end{align*}

具体的な数字で計算を行いましょう。

【例1】

2次正方行列$A=\begin{pmatrix}
1 &2\\
3 & 4
\end{pmatrix}\\$の行列式を考えましょう。

\begin{align*}
|A|&=\begin{vmatrix}
1 &2\\
3 & 4
\end{vmatrix}\\
&=1\times 4-2\times 3\\
&=-2
\end{align*}

となります。
行列式$|A|$が0ではないので行列$A$の逆行列が存在します。

【例1】

2次正方行列$A=\begin{pmatrix}
1 &2\\
1 & 2
\end{pmatrix}\\$の行列式を考えましょう。

\begin{align*}
|A|&=\begin{vmatrix}
1 &2\\
1 & 2
\end{vmatrix}\\
&=1\times 2-2\times 1\\
&=0
\end{align*}

となります。
行列式$|A|$が0なので行列$A$の逆行列が存在しません。

カマキリ

2次の正方行列の行列式は簡単ですね。

3次正方行列（サラスの公式）

3次正方行列$A=\begin{pmatrix}
a_{11} &a_{12} & a_{13} \\
a_{21} &a_{22} & a_{23} \\
a_{31} &a_{32} & a_{33} \tag{3}
\end{pmatrix}$の行列式を考えましょう。

3次の正方行列の行列式の計算にはサラスの公式というとても便利な公式があります。

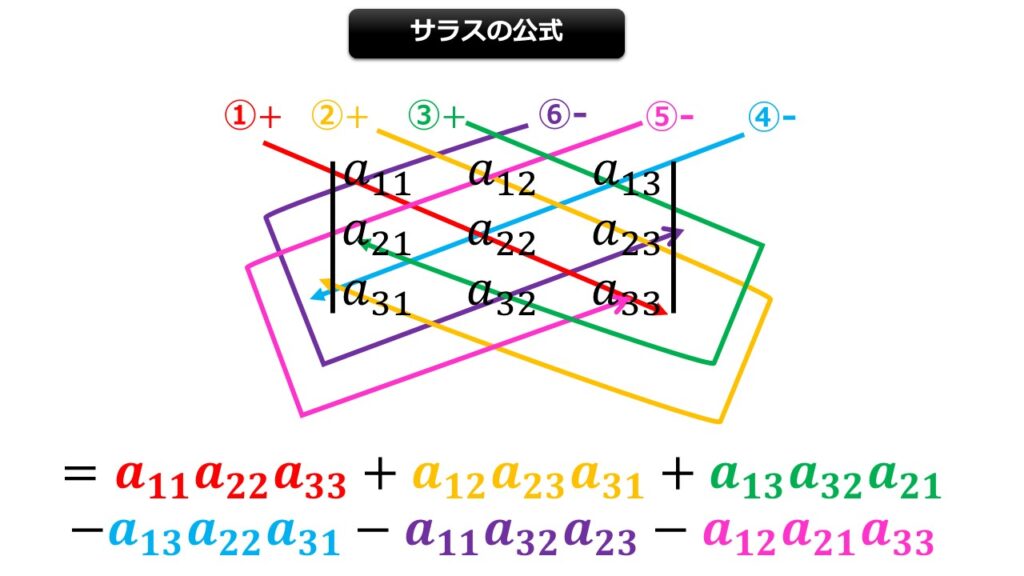
上の絵を見ながら計算を行えば3次正方行列に対しても行列式が計算できます。

\begin{align*}
|A|&=\begin{vmatrix}
a_{11} &a_{12} & a_{13} \\
a_{21} &a_{22} & a_{23} \\
a_{31} &a_{32} & a_{33} \\
\end{vmatrix}\\
&=a_{11} a_{22} a_{33}+a_{12} a_{23}a_{31}+a_{13}a_{32}a_{21}\\
&-a_{13}a_{22} a_{31}-a_{11}a_{32} a_{23} -a_{13}a_{21}a_{33}\tag{6}
\end{align*}

「3つの要素を掛け算して3回足して、次に3つの要素を掛け算して3回引く」という要領で計算を行います。

では、具体的な数字で計算を行いましょう。

【例1】

3次正方行列$A=\begin{pmatrix}
1 &2 & 3\\
4 &5 & 6\\
7 &8 & 9\\
\end{pmatrix}\\$の行列式を考えましょう。

\begin{align*}
|A|&=\begin{vmatrix}
1 &2 & 3\\
4 &5 & 6\\
7 &8 & 9\\
\end{vmatrix}\\
&=1\times 5\times 9+2\times 6\times 7+3\times 8\times 4\\
&-3\times 5\times 7-2\times 4\times 9-1\times 8\times 6\\
&=0
\end{align*}

となります。
行列式$|A|$が0なので行列$A$の逆行列が存在しません。

カマキリ

３次の正方行列の行列式は「サラスの公式」を使えば簡単ですね。