こんにちは(@t_kun_kamakiri)(^^)/
前回では、「転置行列の性質」についての記事をまとめました。
今回は行列式について解説を行います。
- 行列式の定義
- なぜ行列式を計算するのか
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事を読むと「なぜ行列式を計算するのか?」が理解できるようになります(^^)/
なぜ行列式を考えるのか?
本記事では行列式についてお話ししますが、そもそもなぜ行列式を考えなくてはいけないのでしょうか?
$n$次の正方行列$A$に対して$XA=E$(※$E$は単位行列)となるような行列$X$を$A$の逆行列と言います。
XA=E\tag{1}
\end{align*}
そして行列$A$の逆行列を$A^{-1}$と表記します。
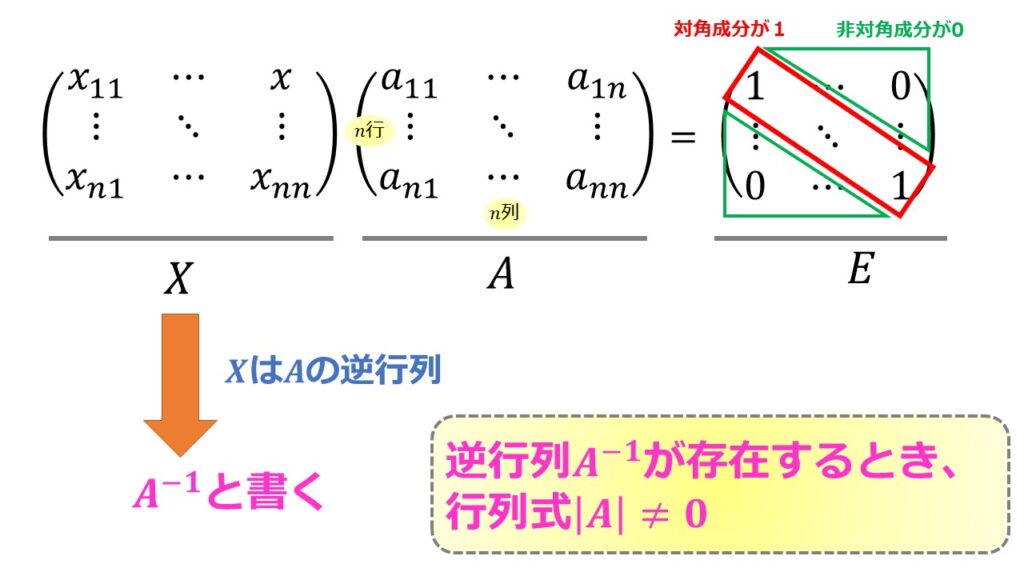
いつでも上記のように行列$A$の逆行列$A^{-1}$が存在するとは限りません。
行列$A$の逆行列が存在するときを特に正則行列と言います。
XA=E\tag{1}
\end{align*}
ここで逆行列が存在するかどうかの判断に行列式が関わってくるというわけです。
$A$の行列式は$|A|$もしくは$det(A)$と表記します。
※detは逆行列の英単語determinantの略です。
ここでは行列式は$|A|$や$det(A)$と書くのか~と思っていればOKです。
実は逆行列が存在するかどうかの判断に本記事で扱う行列式が重要になってきます。
まず結論を以下に述べておきます。
\left\{\begin{matrix}
\left | A \right |\neq 0のとき Aは正則\rightarrow 逆行列A^{-1}が存在する\\
\left | A \right |= 0のとき Aは正則ではない\rightarrow 逆行列A^{-1}が存在しない
\end{matrix}\right.
\end{align*}
※行列式と聞くと「方程式」のような式の形を思い浮かぶかもしれませんが、式ではなく行列式は「$1,\frac{3}{2},-5,0$」などのように値です。
行列式を計算した結果が「0」か「0でないか」で逆行列$A^{-1}$が存在するかどうかの判断に使えるわけですね。
行列$A$の行列式$|A|$を計算して0ならば逆行列$A^{-1}$が存在せず、よって(1)のような単位行列にするような$X=A^{-1}$が存在しないということですね。
逆行列が存在するかどうかを知るために行列式を計算するのがとても重要だということが理解できればひとまずOKです。
逆行列とは$a÷a=1$のイメージ
行列の計算には割り算というものが存在しません。
さらに行列の掛け算は、数の掛け算とは計算方法が違っています。
- 数$a$に対して逆数が存在する場合($xa=1$となる$x$が存在する)、逆数は$x=a^{-1}=\frac{1}{a}$と書きます。
- 行列$A$に対して逆行列が存在する場合($XA=E$となる$X$が存在する)、逆行列は$X=A^{-1}$($\frac{1}{A}$とは書かない)と書きます。
数のように$A÷A=E$のような書き方はせず、$A^{-1}A=AA^{-1}=E$といったように左か右から逆行列を作用させて行列の掛け算として計算を行います。
逆行列が存在するとはどういうことか?イメージで解説する
行列式が0ではない、すなわち逆行列が存在するというのはどういうイメージなのかを絵で説明します。
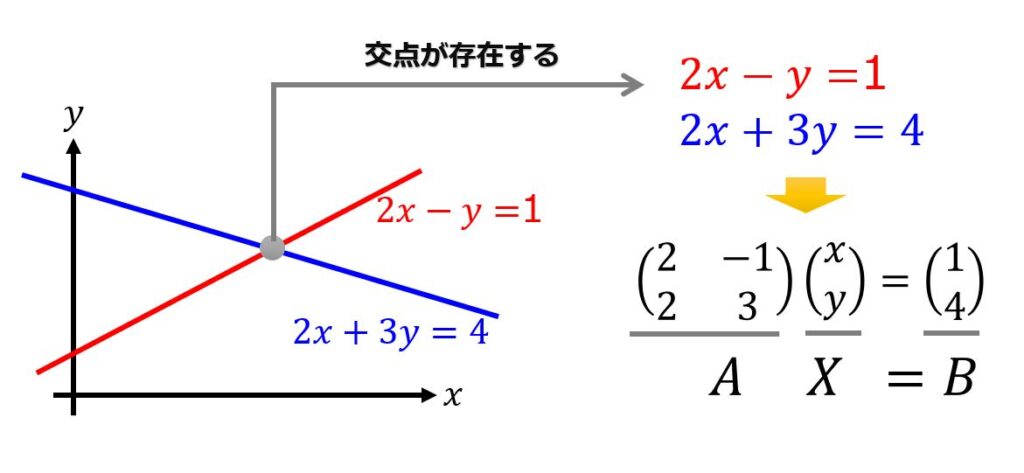
2つの式の連立方程式を考えます。
\left\{\begin{matrix}
2x-y=1\\
2x+3y=4
\end{matrix}\right.
\end{align*}
こちらの連立方程式の解$(x,y)$について図示すると以下の絵のようになり、解は2つの直線の交点であることがわかります。

行列$A$に逆行列が存在する場合は、両辺に左から逆行列を掛けると、
\underset{単位行列E}{A^{-1}A}X=A^{-1}B\\
X=A^{-1}B
\end{align*}
となり行列$X$が求まります。
行列$X$の各要素$(x,y)$が図示した直線の交点であり、連立方程式の解というわけです。
連立方程式の解が存在するかどうかというのは、変数の数に対して同じ数だけ独立な式が必要です。
- 変数の数:$x,y$の2つ
- 独立な式:2つあれば解が存在する
なので、正方行列ではない場合の行列(例えば2行3列の行列)は、変数の数と式の数が同じではないので逆行列を定義することができないわけですね。
逆行列が存在しないとはどういうことか?イメージで解説する
では、逆行列が存在しない場合というのはどういう状況下を絵にしてみます。
連立方程式の解が存在するかどうかというのは、変数の数に対して同じ数だけ独立な式が必要です。
片方の式に何倍か掛けただけの式を用意しても独立な式とは言えません。
この場合は2つの直線が平行になって交わることはありません。
- 変数の数:$x,y$の2つ
- 独立な式ではない
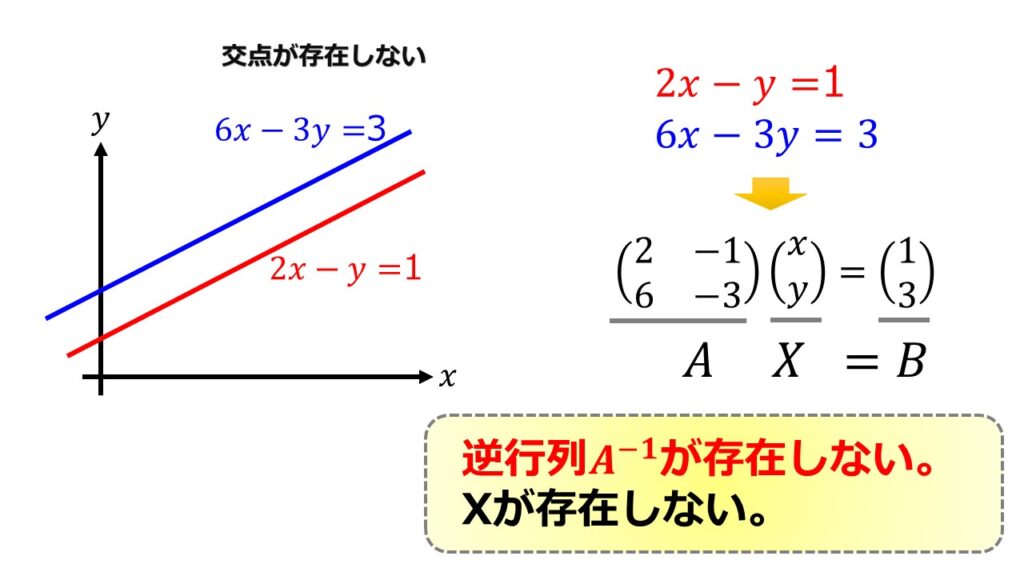

この図から解は存在しないことがわかります。
そして、行列式を計算すると0であることもわかり逆行列が存在しないということになります。
同様に全く同じ式を2つ用意しても、それは独立な式ではないため直線が重なってしまい解が無数に存在することになり1つの解には定まりません。
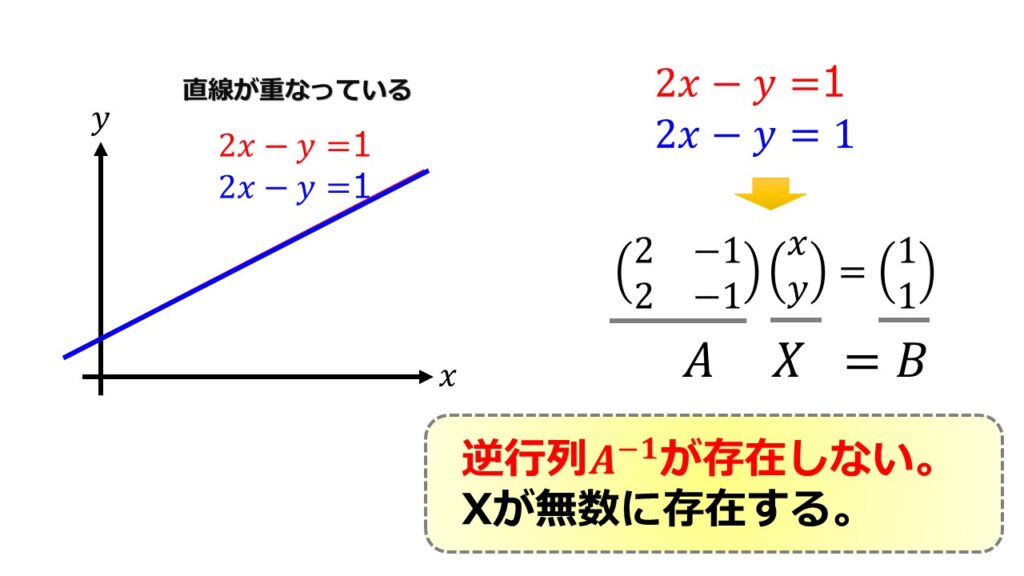

こちらも行列式を計算すると0であることもわかり逆行列が存在しないということになります。
まとめ
行列式は正則行列に対して定義できるものであるということを覚えておきましょう(^^)/
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/