線形独立と線形従属をわかりやすく解説

本記事では線形独立と線形従属について、線形代数の学び始めた人にもわかりやすく解説を行います。

線形独立と線形従属に関して先に結論をまとめておきます。

本記事では一般化のために$n$次元ベクトルについて考えますが。

しかし、線形独立と線形従属を理解するにあたっては次元を落として2次元ベクトルを用いて図でイメージした方が良いでしょう。

下図のように2次元でベクトル$\boldsymbol{e}_{1}=\begin{pmatrix}
1 \\
0
\end{pmatrix}$,$\boldsymbol{e}_{2}=\begin{pmatrix}
0 \\
1
\end{pmatrix}$と$\boldsymbol{a}=\begin{pmatrix}
c_{1} \\
c_{2}
\end{pmatrix}$が存在するとします。

結論

$\boldsymbol{e}_{1}$と$\boldsymbol{e}_{2}$のベクトルは互いに独立で、$\boldsymbol{e}_{1}$は$\boldsymbol{e}_{2}$を使って書くことができないし、$\boldsymbol{e}_{2}$は$\boldsymbol{e}_{1}$を使って書くことができません。
このような関係があるとき、$\boldsymbol{e}_{1},\boldsymbol{e}_{2}$は線形独立（または1次独立）と言います。
$\boldsymbol{e}_{1}$と$\boldsymbol{e}_{2}$と$\boldsymbol{a}$を考えた場合、$\boldsymbol{a}$は$\boldsymbol{e}_{1}$と$\boldsymbol{e}_{2}$を使って$\boldsymbol{a}=c_{1}\boldsymbol{e}_{1}+c_{2}\boldsymbol{e}_{2}$のように表すことができます（$\boldsymbol{e}_{1}$と$\boldsymbol{e}_{2}$についても同様）。このような関係があるとき、$\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{a}$は線形従属（または1次従属）と言います。
要するに互いに独立なベクトルではなく、どれかの線形結合で書けるということです。

以上、結論を先に書きました。

本記事ではもう少し詳しく$n$次元ベクトルでの線形独立と線形従属についての解説を行います。

本記事の内容

線形独立と線形従属をわかりやすく解説

これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。

こんな人が対象

行列をはじめて習う高校生・大学生
仕事で行列を使うけど忘れてしまった社会人

この記事の内容をマスターして線形独立と線形従属を理解しましょう(^^)

線形空間
1. 集合における元
2. 線形空間
線形結合と線形関係式
1. 線形結合
2. 線形関係式
線形独立と線形従属とは
1. 線形独立
2. 線形従属
まとめ
参考にする参考書はこれ

線形空間

線形独立と線形従属を解説する前に線形空間（ベクトル空間）について解説を行います。
扱うベクトルが今から解説する性質を備えているということを認識しながら、線形独立と線形従属を理解する必要があります。

カマキリ

覚える必要はありません。よくわからない場合はひとまず飛ばしても構いません。

集合における元

集合$\boldsymbol{V}$の元（げん）であるベクトル$\boldsymbol{x}$,$\boldsymbol{y}$を考えます。
元という用語に馴染みがないとわかりにくいかもしれませんが、集合における個々の要素と考えてもらえれば良いです。

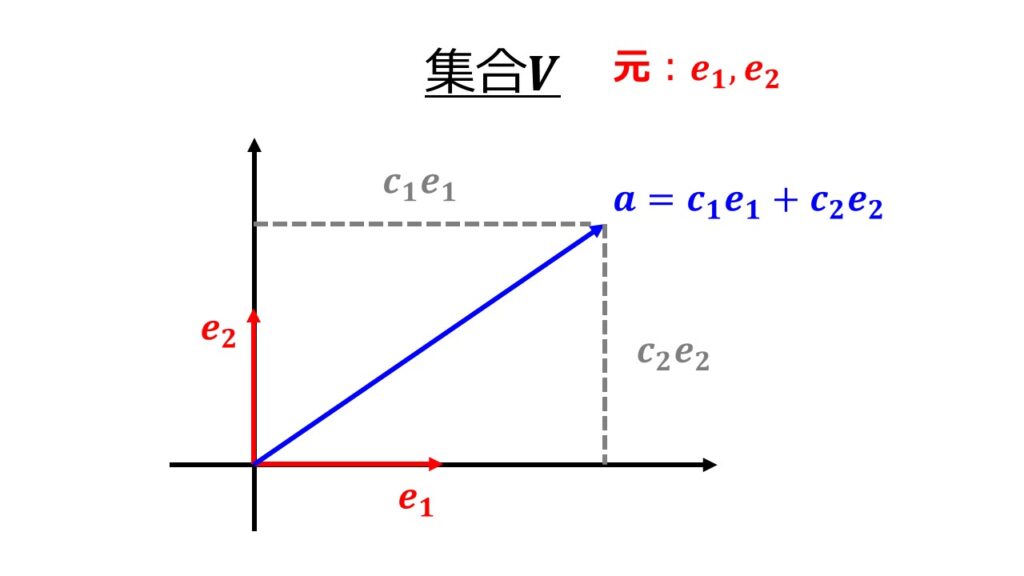
例えば2次元空間で考えた場合、2次元での任意のベクトル$\boldsymbol{x}$を表すのに空間の要素となるベクトルは絵の中の$\boldsymbol{e}_{1}$と$\boldsymbol{e}_{2}$になります。
そして、任意のベクトル$\boldsymbol{x}$は$\boldsymbol{x}=c_{1}\boldsymbol{e}_{1}+c_{2}\boldsymbol{e}_{2}$のように線形結合（1次結合ともいう）で書き表すことができます。

ちなみに上の絵のように元は必ず互いに直交($\boldsymbol{e}_{1}\cdot\boldsymbol{e}_{2}=0$)している必要はありません。

以下のように斜めを向いているベクトルも2次元空間ベクトルの元を成すことができます。

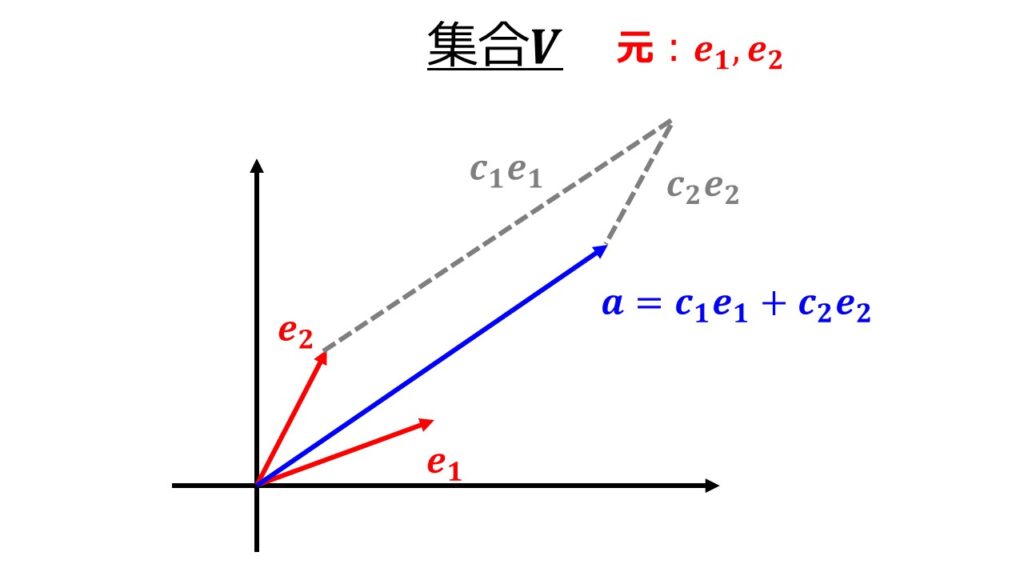
今考えている集合$\boldsymbol{V}$というのが、後ほど説明する線形空間（ベクトル空間）ですので、集合の要素となる元は全てベクトルということになります。

簡単に言うと「線形空間（ベクトル空間）は空間を作るためのベクトルの集まりなんだな」と思ってもらえればOKです。

線形空間

集合$\boldsymbol{V}$の元$\boldsymbol{x}$,$\boldsymbol{y}$に対して以下の条件を満たすとき、集合$\boldsymbol{V}$を線形空間（ベクトル空間）と呼びます。

和の性質

$(\boldsymbol{x}+\boldsymbol{y})+\boldsymbol{z}=\boldsymbol{x}+(\boldsymbol{y}+\boldsymbol{z})$：結合法則
$\boldsymbol{x}+\boldsymbol{y}=\boldsymbol{y}+\boldsymbol{x}$：交換法則
零ベクトル$\boldsymbol{0}$と呼ばれるベクトルがただ一つ存在する。任意の$\boldsymbol{x}$に対して$\boldsymbol{x}+\boldsymbol{0}=\boldsymbol{0}+\boldsymbol{x}$が成り立つ
$\boldsymbol{V}$の任意の元$\boldsymbol{x}$に対して$\boldsymbol{x}+\boldsymbol{x}^{\prime}=\boldsymbol{0}$となる$\boldsymbol{x}^{\prime}$(逆ベクトル)がただ一つ存在する。

スカラー倍の性質
※任意の実数$a,b$

$(a+b)\boldsymbol{x}=a\boldsymbol{x}+b\boldsymbol{x}$
$a(\boldsymbol{x}+\boldsymbol{y})=a\boldsymbol{x}+a\boldsymbol{y}$
$(ab)\boldsymbol{x}=a(b\boldsymbol{x})$
$\boldsymbol{1}\cdot\boldsymbol{x}=\boldsymbol{x}$

なんだかよくわからないような当たり前のような不思議な感じですが、線形空間（ベクトル空間）は上記のような性質を持っているということを頭に入れておく必要があります。

ベクトルについては次元があるため、例えば列ベクトル$\boldsymbol{x}$して

■2次元ベクトル：$\boldsymbol{x}=\begin{pmatrix}
x_{1} \\
x_{2}
\end{pmatrix}$の集合は$\boldsymbol{R}^{2}$

■3次元ベクトル：$\boldsymbol{x}=\begin{pmatrix}
x_{1} \\
x_{2}\\
x_{3}\end{pmatrix}$の集合は$\boldsymbol{R}^{3}$

■$\cdots$

■$n$次元ベクトル：$\boldsymbol{x}=\begin{pmatrix}
x_{1} \\
x_{2}\\
\cdots\\
x_{n}
\end{pmatrix}$の集合は$\boldsymbol{R}^{n}$

と書くことができます。
集合は$\boldsymbol{R}^{n}$は実数の集まりですが、上記のような集合に対しては複素数全体の集合$\boldsymbol{C}$に対しても同じことが言えます。

基礎数学1線型代数入門

齋藤正彦

1,683円(04/25 10:06時点)

発売日: 2019/03/08

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

↑こちらの参考書では実数全体の集合$\boldsymbol{R}$と複素数全体の集合$\boldsymbol{C}$をまとめて集合$\boldsymbol{K}$と書いていますので、集合$\boldsymbol{K}$を見かけたら「実数と複素数の集合を統一しているんだな～」って思えば良いです。

ベクトルは高校生でも習いますので、上記の性質はむしろ当たり前になっているかもしれません。改めて性質を見せられても新しく学ぶことがないと思いますが、ベクトルの性質として再度認識をしておきましょう。

線形結合と線形関係式

では次に線形結合と線形関係式について解説を行います。

線形結合

先ほど定義した線形空間（ベクトル空間）の集合$\boldsymbol{V}$には$n$個のベクトル${\boldsymbol{a}_{1},\boldsymbol{a}_{2},\cdots,\boldsymbol{a}_{n}}$があるとします。

これらに対して以下の形のベクトルを考えます。

\begin{align*}
c_{1}\boldsymbol{a}_{1}+c_{2}\boldsymbol{a}_{2}+\cdots +c_{n}\boldsymbol{a}_{n}\tag{1}
\end{align*}

※$c_{i}(i=1,2,\cdots,n)$は実数（もしくは複素数）

(1)を線形結合と言います。

カマキリ

用語だけ覚えておけばよいでしょう

$n$次元ベクトルだとちょっとわかりにくいなーと思ったら2次元ベクトルで考えてみ見れば良いですね。先ほどの絵を使って2次元ベクトルでの線形結合のイメージを書くと以下となります。

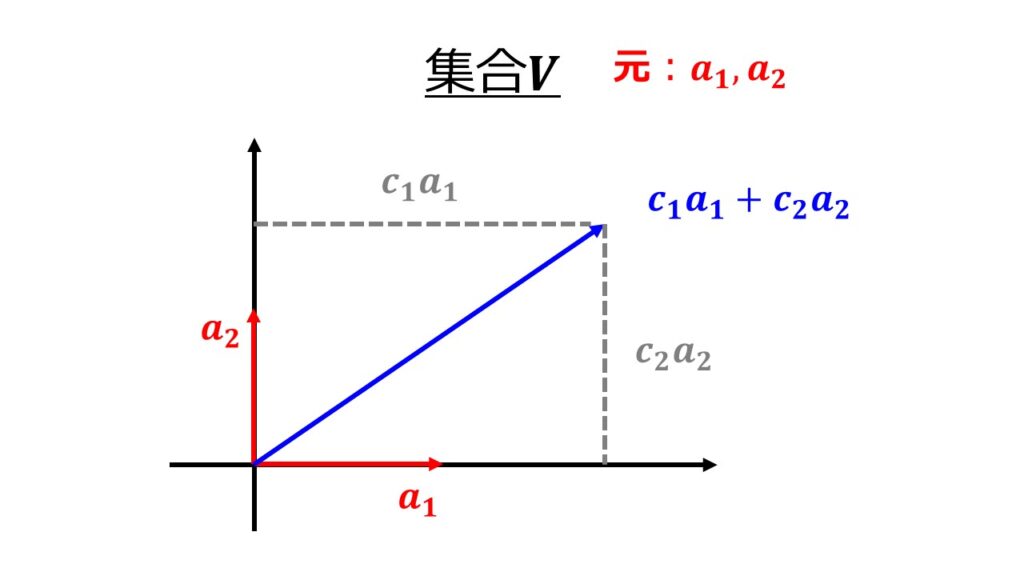
線形関係式

先ほどの線形結合が0になる関係式を線形関係式と言います。

\begin{align*}
c_{1}\boldsymbol{a}_{1}+c_{2}\boldsymbol{a}_{2}+\cdots +c_{n}\boldsymbol{a}_{n}=\boldsymbol{0}\tag{2}
\end{align*}

※$c_{i}(i=1,2,\cdots,n)$は実数（もしくは複素数）

この線形関係式に対して、以下で解説するような線形独立か線形従属かを定義することができます。

カマキリ

線形関係式は頭に入れておきましょう

線形独立と線形従属とは

線形関係式の係数によって線形独立か線形従属化かが決まります。

線形独立

\begin{align*}
c_{1}\boldsymbol{a}_{1}+c_{2}\boldsymbol{a}_{2}+\cdots +c_{n}\boldsymbol{a}_{n}=\boldsymbol{0}\tag{2}
\end{align*}

※$c_{i}(i=1,2,\cdots,n)$は実数（もしくは複素数）

に対して、$c_{1}=c_{2}=\cdots =c_{n}=0$のときのみ(2)が成り立つとき、${\boldsymbol{a}_{1},\boldsymbol{a}_{2},\cdots,\boldsymbol{a}_{n}}$は線形独立（1次独立）といいます。

イメージをつかむために、3次元空間を例にとります。線形独立な組として${\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3}}$を考えます。各々が$x$,$y$,$z$方向に向いている単位ベクトルを考えます。

このとき${\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3}}$は線形独立なので、例えば$\boldsymbol{e}_{2}$と$\boldsymbol{e}_{3}$を使って$\boldsymbol{e}_{1}$を表そうとしたときに、どう頑張っても表すことができませんよね。
絵のように、$\boldsymbol{e}_{2}$と$\boldsymbol{e}_{3}$を使って表すことができるのは$y-z$平面の任意のベクトルのみで、$x$方向に成分を持つベクトルを表現することができませんね。

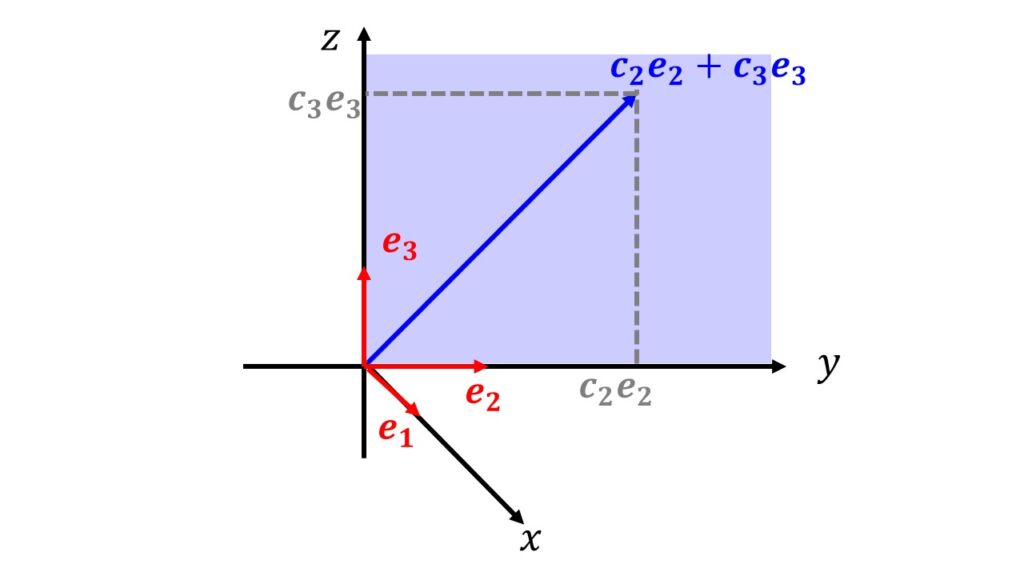
線形独立というのは、各々が向きを表すのに欠かせない役割を担っているということになります。上の例に$e_{1}$を加ええると、3次元空間を考えた時に${\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3}}$は線形独立なので、任意のベクトルは$c_{1}\boldsymbol{e}_{1}+c{2}\boldsymbol{e}_{2}c_{3}\boldsymbol{e}_{3}$と表現することができます。

このように空間を表現するのにもとになるベクトルの組を基底といいます。

では、基底についてまとめておきます。

線形空間の基底

線形空間$V$の元の組${\boldsymbol{a}_{1},\boldsymbol{a}_{2},\cdots,\boldsymbol{a}_{n}}$は線形独立（1次独立）であるとき、これらの組を線形空間$V$の基底と呼ぶ。

任意のベクトル$\boldsymbol{x}$は、

\begin{align*}
\boldsymbol{x}=c_{1}\boldsymbol{a}_{1}+c_{2}\boldsymbol{a}_{2}+\cdots +c_{n}\boldsymbol{a}_{n}\tag{3}
\end{align*}

※$c_{i}(i=1,2,\cdots,n)$は実数（もしくは複素数）

と書ける。

基底は空間を作るためにもとになるベクトルであるということですね。

一点注意ですが、上の絵では基底として互いに直交している単位ベクトルの組${\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3}}$を考えましたが、線形空間の基底を成すものとして互いに直交している必要はありませんし、大きさが１（単位ベクトル）である必要もありません。

線形従属

線形独立は線形関係式において$c_{1}=c_{2}=\cdots=c_{n}=0$のときでしたが、線形従属は以下の場合になります。

$c_{1},c_{2},\cdots,c_{n}$の少なくとも１つは0でない場合、${\boldsymbol{a}_{1},\boldsymbol{a}_{2},\cdots,\boldsymbol{a}_{n}}$は線形従属（1次従属）といいます。

少々わかりにくいので次元を落として(3)の場合を考えます。

簡単に言うと

\begin{align*}
c_{1}\boldsymbol{a}_{1}+c_{2}\boldsymbol{a}_{2}+c_{3}\boldsymbol{a}_{3}+c_{4}\boldsymbol{a}_{4}=\boldsymbol{0}\tag{3}
\end{align*}

と書かれているとき、「係数の少なくとも1つは０ではないときに、どれかのベクトルの組で別のベクトルを表すことができますよ」ということです。

どういうことかと言うと、係数のどれかが０ではないということなので(3)で$c_{4}\neq 0$とします。

\begin{align*}
\boldsymbol{a}_{4}=-\frac{c_{1}}{c_{4}}\boldsymbol{a}_{1}-\frac{c_{2}}{c_{4}}\boldsymbol{a}_{2}-\frac{c_{3}}{c_{4}}\boldsymbol{a}_{3}\tag{4}
\end{align*}

と書くことができます。

こんな感じで、$\boldsymbol{a}_{4}$に関しては別のベクトルの組を使って表現することができるわけです。

絵にするとこんな感じ。

カマキリ

絵を描くとわかりやすいです。

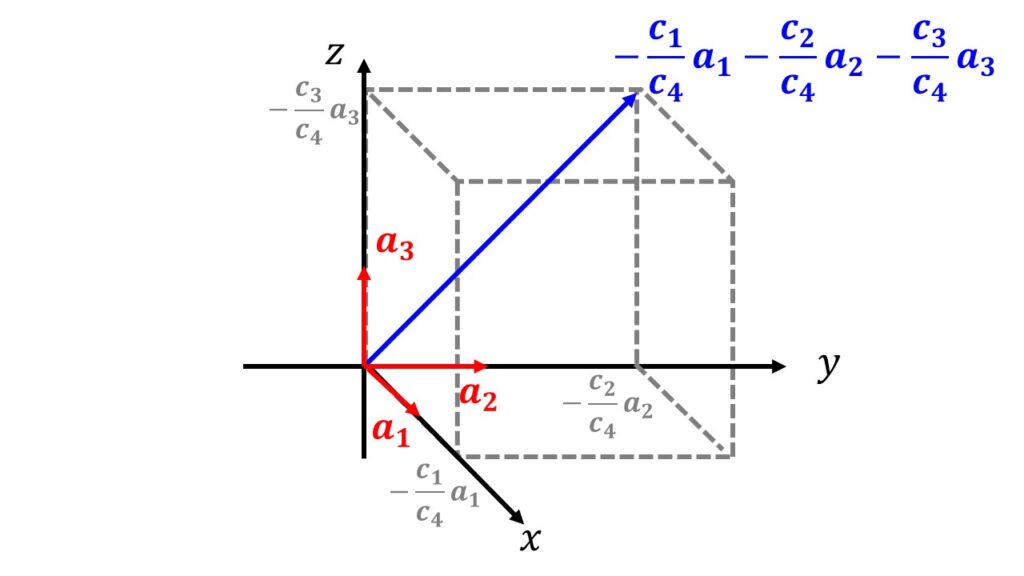
基底となるベクトルの組が4組以上になると絵で描くことができませんが、$n$次元ベクトルについても考えることができますね。

まとめ

本記事では線形独立と線形従属を絵を用いながら解説しました。
学んだことをまとめておきます。

線形関係式

\begin{align*}
c_{1}\boldsymbol{a}_{1}+c_{2}\boldsymbol{a}_{2}+\cdots +c_{n}\boldsymbol{a}_{n}=\boldsymbol{0}\tag{2}
\end{align*}

※$c_{i}(i=1,2,\cdots,n)$は実数（もしくは複素数）

線形独立と線形従属

$c_{1}=c_{2}=\cdots =c_{n}=0$のときのみ(2)が成り立つとき、${\boldsymbol{a}_{1},\boldsymbol{a}_{2},\cdots,\boldsymbol{a}_{n}}$は線形独立（1次独立）といいます。
$c_{1},c_{2},\cdots,c_{n}$の少なくとも１つは0でない場合、${\boldsymbol{a}_{1},\boldsymbol{a}_{2},\cdots,\boldsymbol{a}_{n}}$は線形従属（1次従属）といいます。

カマキリ

次回お楽しみに！