こんにちは(@t_kun_kamakiri)(^^)/
前回の記事では基底変換について解説を行いました。
前回の記事のまとめを書いておきましょう。
基底が$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$での線形変換$A$は、基底を変換する変換行列$P$を用いると、新たな基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$で表したときの成分に対して対応する線形変換は$P^{-1}AP$となります。
基底は変換行列$P$で以下のように変換されます。
$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}=P^{-1}\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}$
もしくは、
$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}=P\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}
\end{pmatrix}$
①$\boldsymbol{x}$を基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$から別の基底$\{\boldsymbol{e}_{1}^{\prime},\boldsymbol{e}_{2}^{\prime}\}$での成分に変換します。
\boldsymbol{y}=P^{-1}\boldsymbol{x}
\end{align*}
②新たな基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$での成分の線形変換は、
\boldsymbol{y}^{\prime}=P^{-1}AP\boldsymbol{y}
\end{align*}
となります。
③元の基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$の成分に戻したい場合は
\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}
\end{align*}
とれば元に戻ります。
元の基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$のまま線形変換$\boldsymbol{x}^{\prime}=A\boldsymbol{x}$の計算は、1回別の基底$\{\boldsymbol{e}^{\prime}_{1},\boldsymbol{e}^{\prime}_{2}\}$での成分で線形変換$\boldsymbol{y}^{\prime}=P^{-1}AP\boldsymbol{y}$を行い、元の基底の成分に戻して$\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}$としても結果は同じということです。
本記事では基底を変えて、線形変換が対角行列になるということを具体的な値を使って計算します。
固有ベクトルを基底に持つ変換行列を用いると、線形変換が対角行列になることを示す
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事の内容をマスターして基底変換に関しての理解を深めましょう(^^)
本記事ではどの基底を使ったときの表現なのかをわかるように書いてきました。以下のルールを適用することで迷子にならずに進めることができます。
- $\boldsymbol{x}=\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}_{e}$：右下に添え字で基底を表記 - $\boldsymbol{x}=\underset{基底がわかる\\ように列ベクトル\\で書く}{\begin{pmatrix}
\boldsymbol{e}_{1}&
\boldsymbol{e}_{2}
\end{pmatrix}}\begin{pmatrix}
x_{1}\\
x_{2}\\
\end{pmatrix}$
このようにルールを決めて進める意義をわかっていただけれたと思います。
まずは$\boldsymbol{x}^{\prime}=A\boldsymbol{x}$を普通に計算
今、基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$での線形変換$A$を考えます。
- $\boldsymbol{e}_{1}=\begin{pmatrix}
1\\
0\\
\end{pmatrix}$と$\boldsymbol{e}_{2}=\begin{pmatrix}
0\\
1\\
\end{pmatrix}$ - 線形変換する行列$A=\begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}$
今、$\boldsymbol{x}=\begin{pmatrix}
3\\
1\\
\end{pmatrix}$のベクトルを線形変換する行列$A=\begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}$によって変換することを考えます。
結果は$\boldsymbol{x}^{\prime}=A\boldsymbol{x}=\begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}\begin{pmatrix}
3\\
1\\
\end{pmatrix}=\begin{pmatrix}
10\\
4
\end{pmatrix}$と計算ができます。
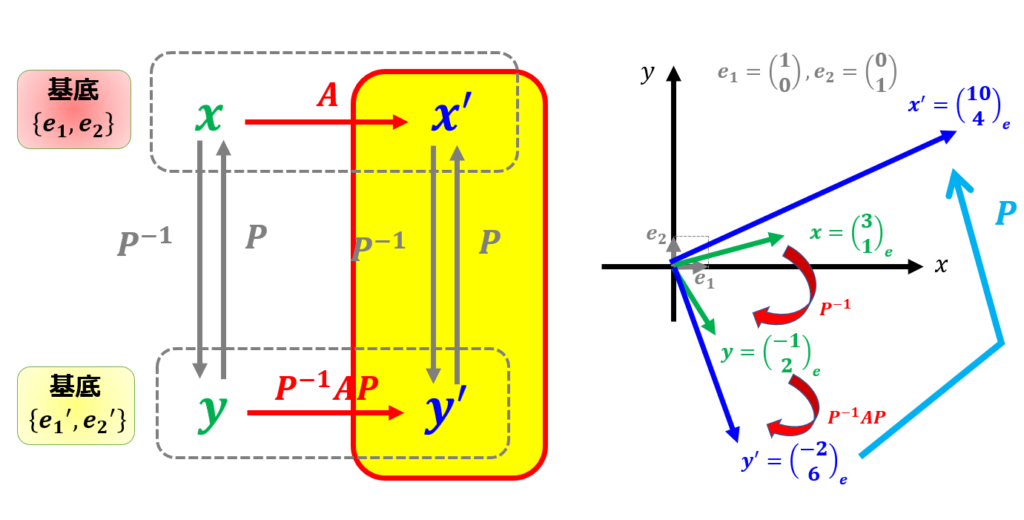
これを図にすると以下のようになります。
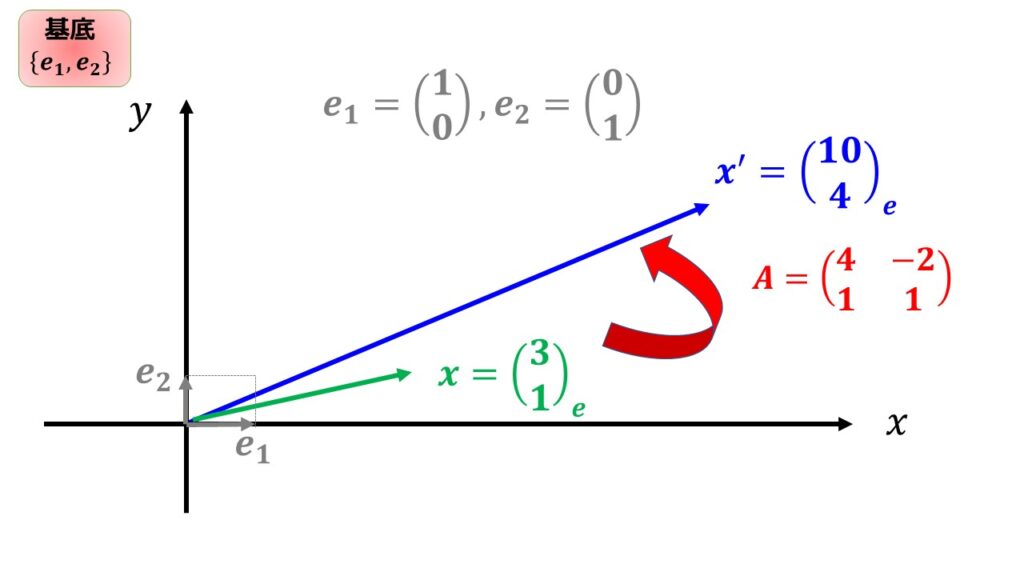
行列の掛け算の計算が面倒ですが、$\boldsymbol{x}$が行列$A$を使って$\boldsymbol{x^{\prime}}$に変換されたのがわかります。ただ普通に行列計算をしただけですが、変換された$\boldsymbol{x^{\prime}}=\begin{pmatrix}
10\\
4\\
\end{pmatrix}$は基底が相変わらず$\boldsymbol{e}_{1}=\begin{pmatrix}
1\\
0\\
\end{pmatrix}$と$\boldsymbol{e}_{2}=\begin{pmatrix}
0\\
1\\
\end{pmatrix}$であることに注意です。
つまり、基底が$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$のまま線形変換$A$によって$\boldsymbol{x^{\prime}}=\begin{pmatrix}
10\\
4
\end{pmatrix}$になったということです。
基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$であるときの$A\boldsymbol{x}$の計算はちょっと面倒ですよね。
ひとつの行列要素で2回掛け算を行い、それが各4つの行列要素にあるため、2×（2×2)の8回掛け算を計算していることになります。
このような行列計算は数値シミュレーション（数値計算）などの演算にも使われるのですが、プログラムでの掛け算は計算時間がかかるため工夫がこのままの基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$を使うのは効率が悪いし、手計算で行うにしても8回も掛け算を行うとどこかで計算ミスが起こりそうです。
基底$\{\boldsymbol{e}_{1}^{\prime},\boldsymbol{e}_{2}^{\prime}\}$に変換
基底を変換して$A$が対角行列になるような基底変換を行うことができればいいですよね。
基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$から$\{\boldsymbol{e}_{1}^{\prime},\boldsymbol{e}_{2}^{\prime}\}$に変換する行列$P$は何がいいでしょうか。
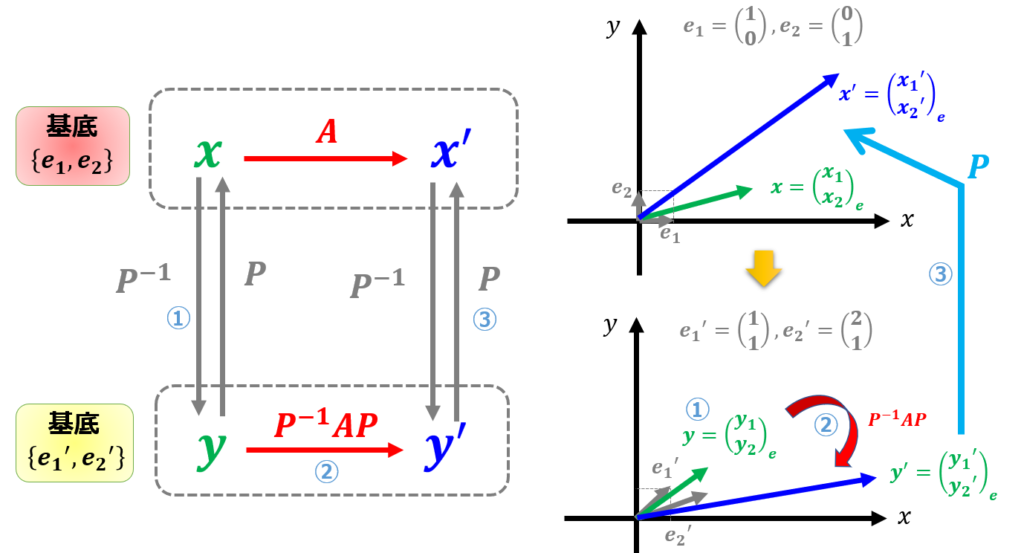
ここで固有値方程式から得られる固有値と固有ベクトルの登場です。
固有値方程式$A\boldsymbol{x}=\alpha \boldsymbol{x}$より
- 固有値$\alpha_{1}$に対応する固有ベクトルは$\boldsymbol{x}_{1}=
\begin{pmatrix}
x_{11}\\
x_{21}\\
\end{pmatrix}$ - 固有値$\alpha_{2}=3$に対応する固有ベクトルは$\boldsymbol{x}_{2}=
\begin{pmatrix}
x_{12}\\
x_{22}\\
\end{pmatrix}$
となったとします。
$\boldsymbol{e}_{1}^{\prime}=\boldsymbol{x}_{1},\boldsymbol{e}_{2}^{\prime}=\boldsymbol{x}_{2}$と置きます。
基底変換行列$P=\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^{\prime}\\
\end{pmatrix}$のように固有値方程式から得られた固有ベクトルを採用します。$\begin{pmatrix}
\boldsymbol{e}^{\prime}_{1}&\boldsymbol{e}^{\prime}_{2}
\end{pmatrix}=P\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}\end{pmatrix}$から$\begin{pmatrix}
\boldsymbol{e}_{1}&\boldsymbol{e}_{2}\end{pmatrix}=E$(単位行列)であることからもわかりますね。
- $A\boldsymbol{e}_{1}^{\prime}=\alpha_{1}\boldsymbol{e}_{1}^{\prime}$
- $A\boldsymbol{e}_{2}^{\prime}=\alpha_{2}\boldsymbol{e}_{2}^{\prime}$
となるので、行列でまとめると、
A\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^{\prime}
\end{pmatrix}&=\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^{\prime}
\end{pmatrix}\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2}
\end{pmatrix}\\
AP&=P\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2}
\end{pmatrix}\tag{1}
\end{align*}
となります。
$A$の異なる固有値に対応する固有ベクトルは線形独立なので、それを基底とする変換行列$P$には逆行列$P^{-1}$が存在します。
よって、両辺左から逆行列$P^{-1}$を掛けて、
\begin{pmatrix}
\alpha_{1} & 0\\
0 & \alpha_{2}
\end{pmatrix}=P^{-1}AP\tag{2}
\end{align*}
となります。
非対角成分が0である対角行列が出てきました。
これは非常に都合が良い結果になりましたね。
上の図を思い出すと、基底$\{\boldsymbol{e}_{1},\boldsymbol{e}_{2}\}$での線形変換$A$を別の基底$\{\boldsymbol{e}_{1}^{\prime},\boldsymbol{e}_{2}^{\prime}\}$に変換した際に対応する線形変換が$P^{-1}AP$だったからです。
だから、基底変換行列$P=\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^{\prime}\end{pmatrix}$を使って別の基底での成分$\boldsymbol{y}=P^{-1}\boldsymbol{x}$に変換して、線形変換$\boldsymbol{y}^{\prime}=P^{-1}AP\boldsymbol{y}$を行い、最後に$\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}$で元の成分に戻せば良いことがわかります。
固有値方程式の固有ベクトルを基底にする
では、冒頭で行った計算$\boldsymbol{x}=\begin{pmatrix}
3\\
1\\
\end{pmatrix}$のベクトルを線形変換する行列$A=\begin{pmatrix}
4 & -2\\
1 & 1
\end{pmatrix}$を固有ベクトルを基底とする系に変換して計算してみましょう。
$\boldsymbol{e}_{1}^{\prime}=\boldsymbol{x}_{1},\boldsymbol{e}_{2}^{\prime}=\boldsymbol{x}_{2}$と置きます。
基底変換行列$P=\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^{\prime}\\
\end{pmatrix}=\begin{pmatrix}
1 &2\\
1 &1
\end{pmatrix}$とします。
まずは、
\boldsymbol{x}&=x_{1}\boldsymbol{e}_{1}+x_{2}\boldsymbol{e}_{2}=
\begin{pmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2}\end{pmatrix}
\begin{pmatrix}
x_{1}\\
x_{2}
\end{pmatrix}\\
&=y_{1}\boldsymbol{e}^{\prime}_{1}+y_{2}\boldsymbol{e}^{\prime}_{2}=\begin{pmatrix}
\boldsymbol{e}^{\prime} &\boldsymbol{e}^{\prime}_{2}\end{pmatrix}\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}
\end{align*}
というように基底を$\{\boldsymbol{e}^{\prime}_{1} ,\boldsymbol{e}^{\prime}_{2}\}$とした際の成分$\begin{pmatrix}
y_{1}\\
y_{2}
\end{pmatrix}$に変換します。
\boldsymbol{y}=P^{-1}\boldsymbol{x}\tag{3}
\end{align*}
変換行列$P=\begin{pmatrix}
1 & 2\\
1 & 1
\end{pmatrix}$は2行2列の行列なので、逆行列は簡単に求まります。
P^{-1}&=\frac{1}{1\times 1-2\times 1}
\begin{pmatrix}
1 & -2\\
-1 & 1
\end{pmatrix}\\
&=\begin{pmatrix}
-1 & 2\\
1 & -1
\end{pmatrix}
\tag{4}
\end{align*}
なので、
\boldsymbol{y}&=\begin{pmatrix}
-1 & 2\\
1 & -1
\end{pmatrix}
\begin{pmatrix}
3 \\
1
\end{pmatrix}\\
&=\begin{pmatrix}
-1 \\
2
\end{pmatrix}
\tag{5}
\end{align*}
※これはあくまで基底$\boldsymbol{e}_{1} ,\boldsymbol{e}_{2}$上での成分の変換であることに注意。
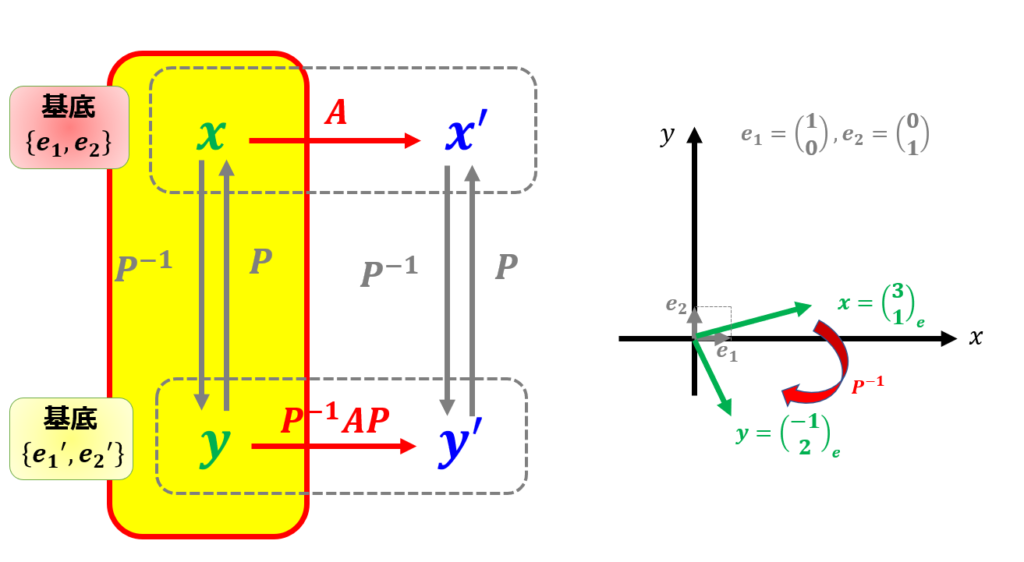
次に、$\boldsymbol{y}^{\prime}=P^{-1}AP\boldsymbol{y}$を計算します。
$P^{-1}AP=\begin{pmatrix}
2 & 0 \\
0 & 3
\end{pmatrix}$であることがわかっているので、この計算は簡単ですね。
\boldsymbol{y}^{\prime}&=\begin{pmatrix}
2 & 0 \\
0 & 3
\end{pmatrix}
\begin{pmatrix}
-1 \\
2
\end{pmatrix}\\
&=\begin{pmatrix}
-2 \\
6
\end{pmatrix}
\tag{6}
\end{align*}
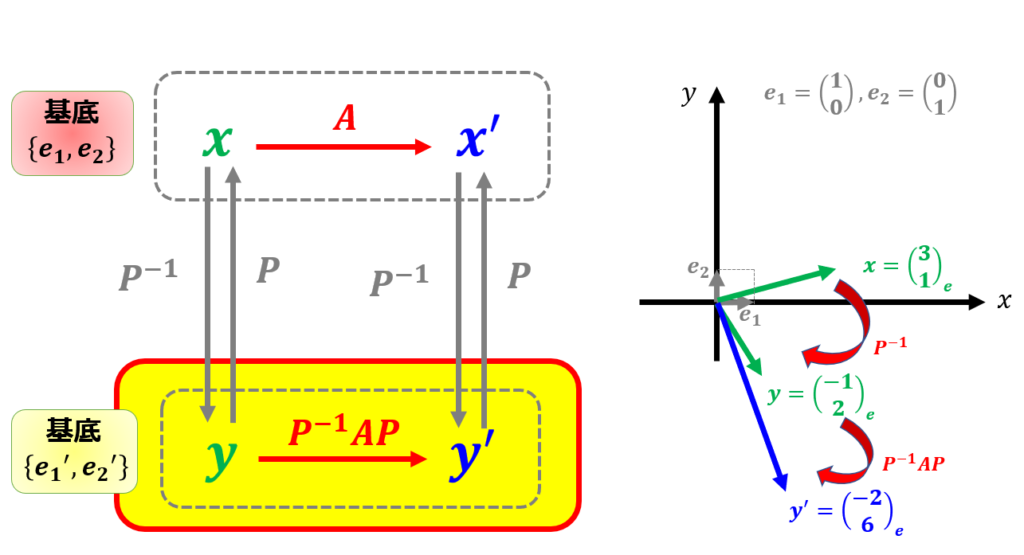
最後に$\boldsymbol{x}^{\prime}=P\boldsymbol{y}^{\prime}$を使って元に戻します。
\boldsymbol{x}^{\prime}&=P\boldsymbol{y}^{\prime}\\
&=\begin{pmatrix}
1 & 2 \\
1 & 1
\end{pmatrix}
\begin{pmatrix}
-2 \\
6
\end{pmatrix}\\
&=\begin{pmatrix}
10 \\
4
\end{pmatrix}
\tag{7}
\end{align*}
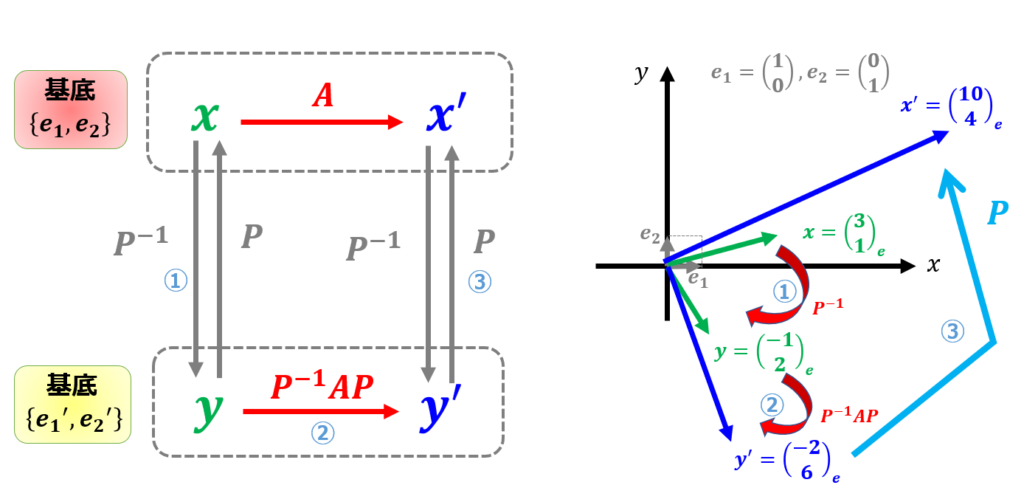
最終的に$\boldsymbol{x}^{\prime}=\begin{pmatrix}
10 \\
4
\end{pmatrix}$となりました。
これは基底変換せずに$\boldsymbol{x}^{\prime}=A\boldsymbol{x}$で計算した結果と同じですね。
まとめ
$\boldsymbol{x}^{\prime}=\begin{pmatrix}
10 \\
4
\end{pmatrix}$の計算を基底変換した成分での変換$\boldsymbol{y}^{\prime}=P^{-1}AP\boldsymbol{y}$を通して計算を行いました。
基底変換行列$P$を固有値方程式$A\boldsymbol{x}=\alpha\boldsymbol{x}$から得られる固有値に対応する固有ベクトルを用いて$P=\begin{pmatrix}
\boldsymbol{e}_{1}^{\prime}&
\boldsymbol{e}_{2}^{\prime}
\end{pmatrix}$ことで、$P^{-1}AP=\begin{pmatrix}
\alpha_{1} & 0 \\
0 & \alpha_{2}
\end{pmatrix}$と対角行列になることを示しました。
参考にする参考書はこれ
当ブログでは、以下の3つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/
Follow @t_kun_kamakiri 
こんにちは イケダと申します。
固有値に対応する固有関数を求める練習をしています。
とてもわかりやすく参考にさせていただきました。ありがとうございました。
’23.02.23