圧縮性流体のベルヌーイの定理

前回、「1次元のオイラーの運動方程式」を導きましたが、今回はそれを使って「ベルヌーイの定理」を紹介したいと思います。

定常な流れを考える

定常な流れとは、\(\frac{\partial v}{\partial t}=0\)のように流速が速度に依存しない流れのことを言います。

だから1次元のオイラーの運動方程式は、

と、なります。

【仮定】

• 1次元
• 非粘性
• 定常流れ

※もちろん非定常な流れでベルヌーイの定理を作ることもできます。

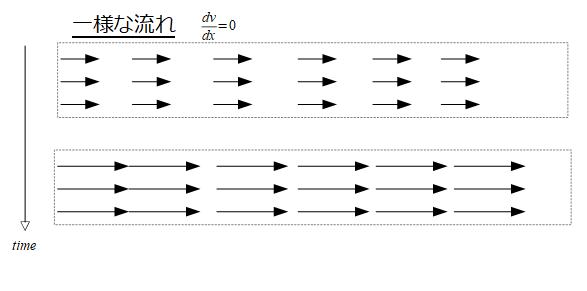
一様な流れ

ここで定常な流れと書きましたが、時間変化しない一様な流れとは違います。

例えば、一様な流れは単に空間に依存しない流れですので全体の流れの様子は空間的には変わりません。

しかし、時間については特に何も言っていないので、時間が経つと全体の流れの様子は変化します。

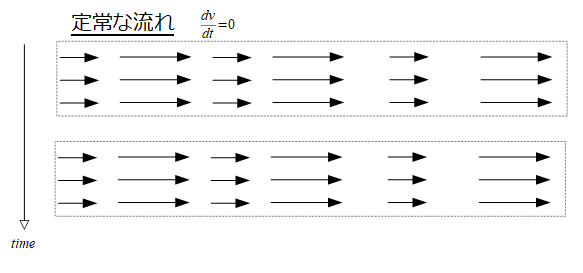
定常な流れ

定常な流れとは、流れの様子が時間によって変化しないと言っているだけで、空間変化はしていても構いません。

積分する

は、定常流れであるため流速も圧力も空間にしか依存していませんので、(1)式は全微分の形で、

と書いても良いでしょう。

※補足

全微分公式

今の場合は、\(v(x),p(x)\)なので、(2)式のようになります。

(2)式を積分することで、ベルヌーイの定理が導けます。

↑これがベルヌーイの定理です。

※costと書いている部分は積分による積分定数です。

まとめ

1次元のオイラーの運動方程式から、ベルヌーイの定理を求めました。

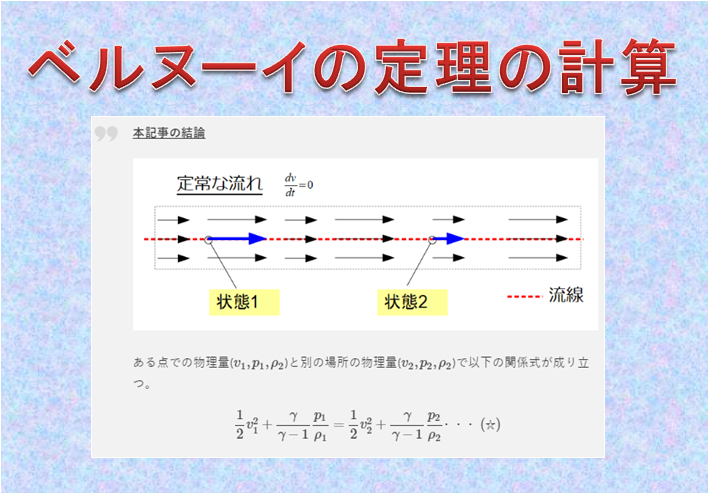
これはある流線に沿って、下記のような2点での(3)式の値が一定値をとるということを意味しています。

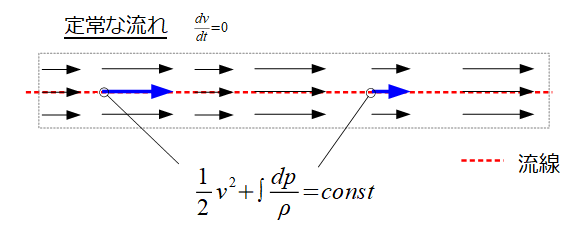
(3)式の第一項を見ればわかるようにこれは「単位質量当たりのエネルギー」を意味しています。

しかし、力学などの質点に対してエネルギー保存則は、時間に関してエネルギーが変わらないというのに対して、上記のベルヌーイの定理は「空間に対してエネルギーが変わらない」ということを意味しています。

ただ、今は定常な流れを考えているので、力学でのエネルギー保存則とベルヌーイの定理は同じことを意味しています。

下記のように青矢印（→）で書いた部分の流体粒子を時間的に追っていくと、流体粒子は流れに沿って別の場所へ移動します。

これは質点の運動を時間的に追っているのと同じであり、その時に(3)が成り立つのであれば、(3)は空間に対してエネルギー保存が成り立つとして導出していながら、実は流れに沿って時間的に変化しないと見ても良いことになります。

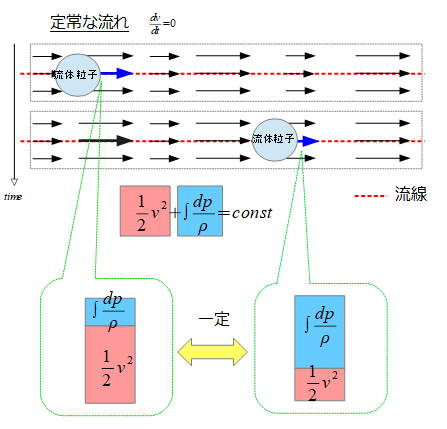
そして、(3)式の各項\(\frac{1}{2}v^2\)と\(\int \frac{dp}{\rho}\)は場所ごとに異なるのですが、和は一定に保たれているというのがベルヌーイの定理の意味です。

次回:「バロトロピー流れ(\(p=p(\rho)\))」

さて、(3)式の第二項\(\int \frac{dp}{\rho}\)さえ積分できれば、あとは手計算で色々と考察をできるのですが、それには圧力\(p\)と密度\(\rho\)の関係式が必要になります。

ここで、熱力学の状態方程式\(f(p,T,\rho=0)\)のような熱力学的変数である圧力\(p\)、温度\(T\)、密度\(\rho\)の関係式を使うことになり、その関係式に従って(3)式を積分することになります。

具体的には、圧力が密度の関数のみである場合の「バロトロピー流れ(\(p=p(\rho)\))」と呼ばれている流れを仮定することになります。

「バロトロピー流れ(\(p=p(\rho)\))」は、

「断熱過程（等エントロピー流れ）、等温過程、非圧縮性の密度一定」の場合にも広く一般的な場合での流れになります。

補足

ベルヌーイの定理の導出の際に、ある仮定（1次元、非粘性、定常）を意識しながら話を進めましたが、1次元でなくても2次元などに拡張したり、非定常な場合でも同様にもっと一般的なエネルギー保存則というのは導出できます。

個人的には、そんな一般系のベルヌーイの定理を用いても解析的に解けないと扱いづらいし、現実の系で一般系を持ち出して議論することも少ないような気もするので、これ以上あまり深くは踏み込みません。

wikipedia:ベルヌーイの定理