等エントロピー流れでのベルヌーイの定理の計算

さていよいよ「ベルヌーイの定理」を具体的に計算していくことになります。

本記事の結論

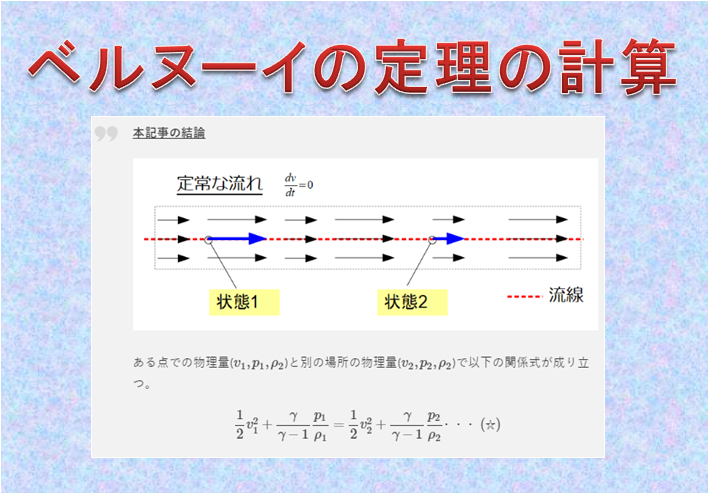
ある点での物理量(\(v_{1},p_{1},\rho_{2}\))と別の場所の物理量(\(v_{2},p_{2},\rho_{2}\))で以下の関係式が成り立つ。

\begin{align*}\frac{1}{2}v_{1}^2+\frac{\gamma}{\gamma-1}\frac{p_{1}}{\rho_{1}}=\frac{1}{2}v_{2}^2+\frac{\gamma}{\gamma-1}\frac{p_{2}}{\rho_{2}}・・・(☆)\end{align*}

復習
等エントロピー流れと仮定
ベルヌーイの定理を積分する
まとめ

復習

今までやったことをまとめると・・・

１．1次元のオイラーの運動方程式

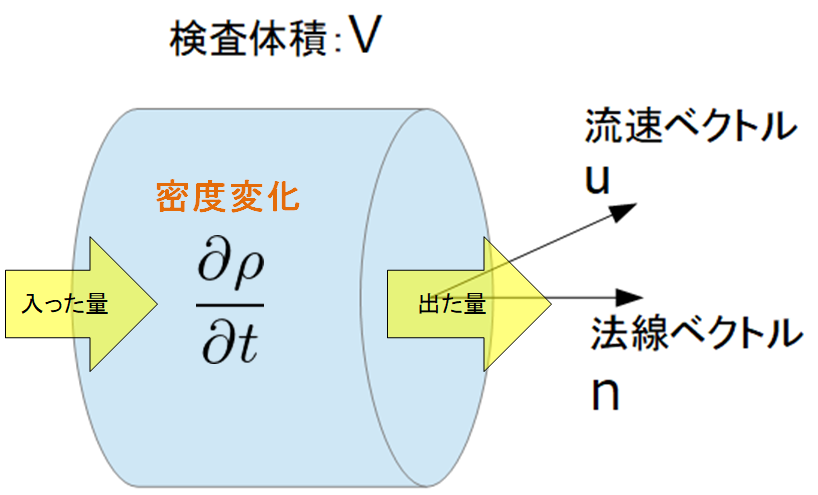
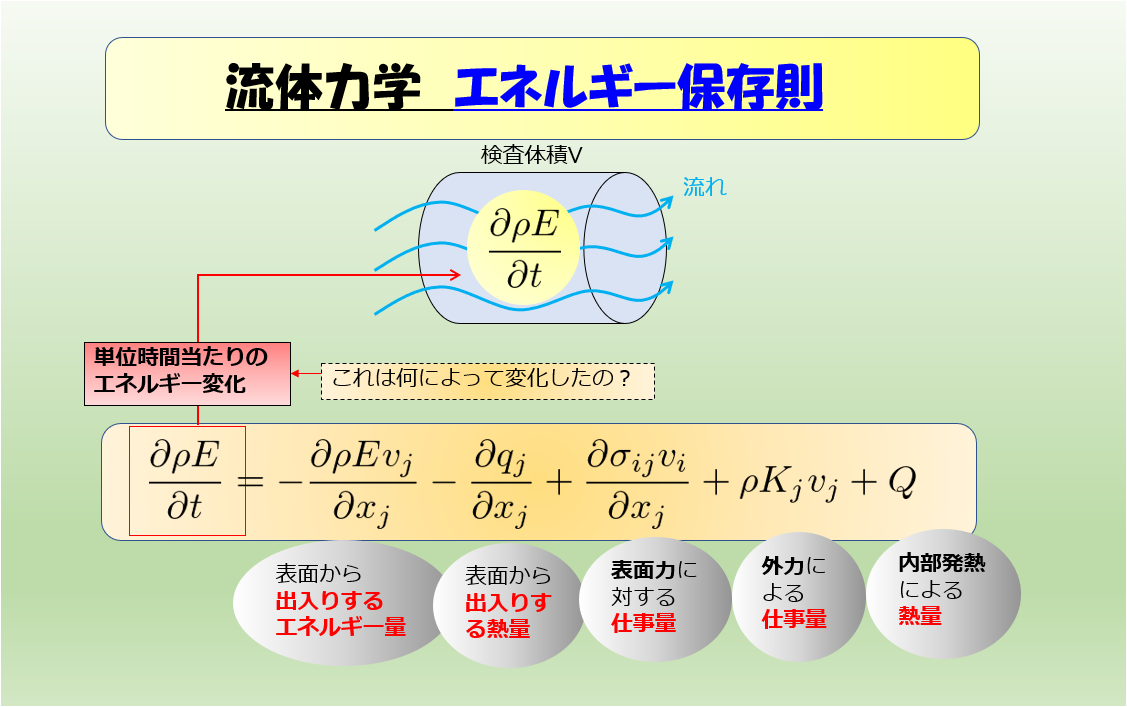
まずある体積空間において運動量保存則より下記の1次元のオイラーの運動方程式を導きました。

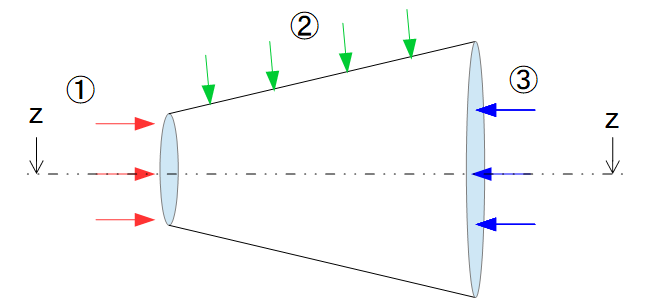
\begin{align*}\frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}=-\frac{1}{\rho }\frac{dp}{dx}・・・(1)\end{align*}

※1次元
※非粘性

２．ベルヌーイの定理

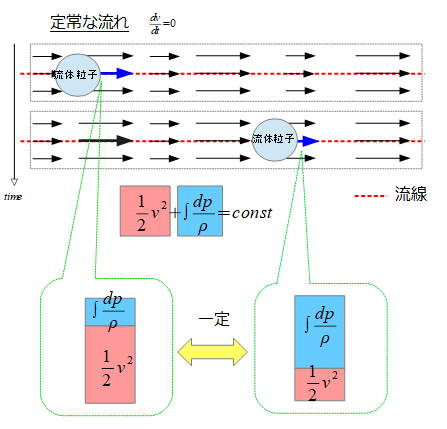
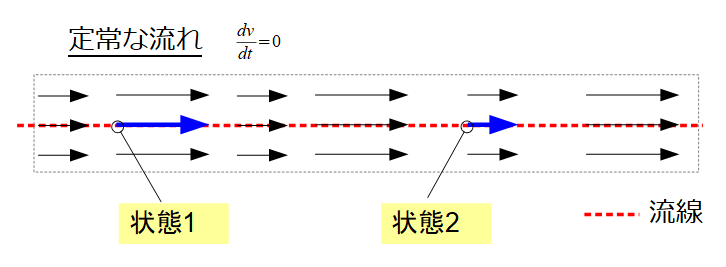
次に、定常な流れ\(\frac{\partial v}{\partial t}=0\)において、ひとつの流線に沿って成り立つ「エネルギー保存則（ベルヌーイの定理）」を導きました。

ベルヌーイの定理

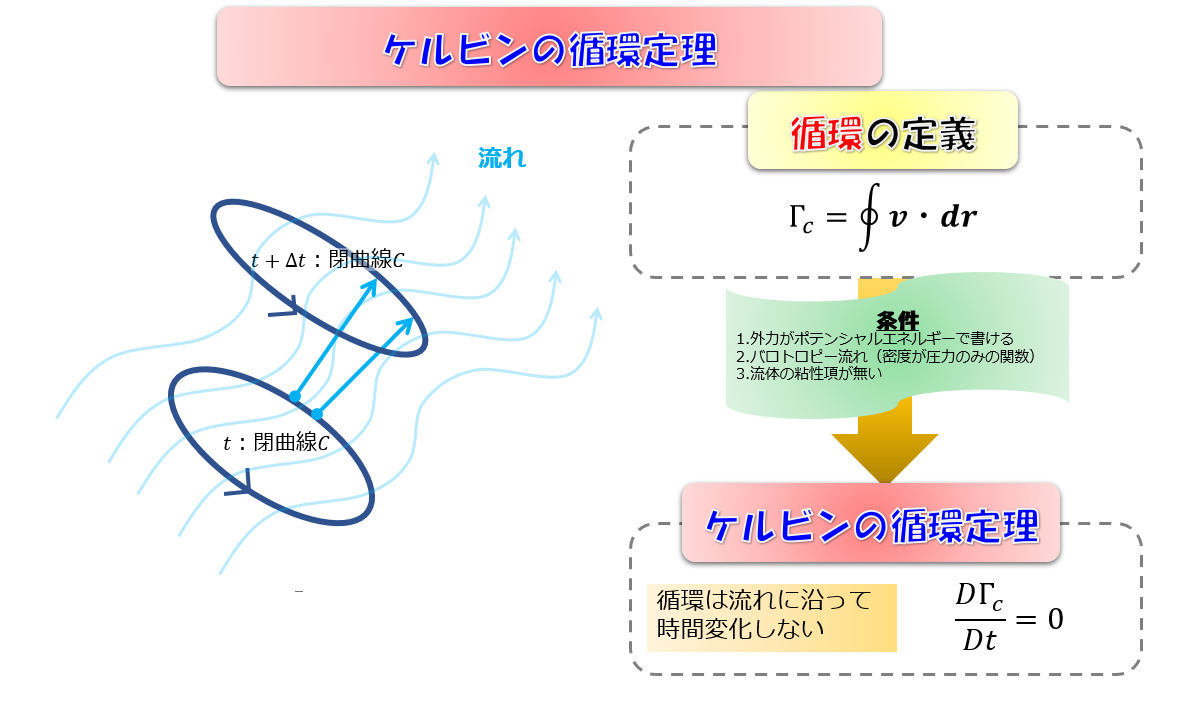
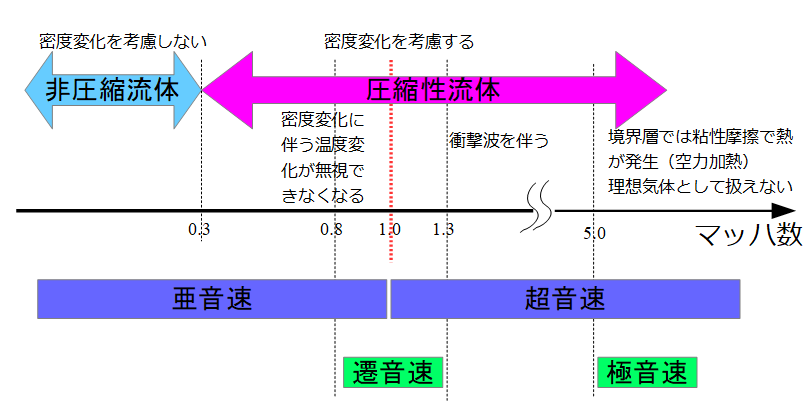
\begin{align*}\frac{1}{2}v^2 +\int \frac{dp}{\rho}=const・・・(2)\end{align*}

３．バロトロピー流れ

バロトロピー流れ：密度が圧力のみの関数

\begin{align*}\rho=\rho (p)・・・(3)\end{align*}

どのような状況下ならばバロトロピー流れと言えるのか？※式は理想気体の場合です。

等エントロピー流れ：\(\frac{p}{\rho^{\gamma}}=const\)

等温過程：\(\frac{p}{\rho}=const\)

密度一定：\(\rho=const\)

では（☆）を導出したいと思います!(^^)!

等エントロピー流れと仮定

まずバロトロピー流れの中でも今考えているのは、等エントロピー流れ、すなわち断熱過程での流れを取り扱うこととします。

もちろん今考えている系において、熱源のような機構は考えていないし、(1)式の「1次元のオイラーの運動方程式」自体に粘性項が存在しないので、エネルギー散逸（エネルギーの逃げ）もありません。

そういう意味で流れは断熱的であると考えても良いでしょう。

あるいは今は1次元の流れを考えていて、yに対するx方向の速度は\(v(y)=一定\)だから、流体間にせん断応力\(\tau =\nu \frac{dv}{dy}\)が発生しないので流体間の摩擦熱は発生しない状況であると考えても良いでしょう。

もう少し詳しく言うと粘性によるエントロピー増加は速度勾配の2乗と粘性係数の積に比例します。

速度勾配が大きい境界層や、速度勾配が小さくても粘性が大きい場合は等エントロピー流れとは言えないということに注意しましょう。

しかし、今考えているのは単純に1次元的に流体が流れているような場合を考えているので、等エントロピー流れと考えてよいでしょう。

そして今は理想気体を考えているとした場合は、断熱過程では、

\begin{align*}\frac{p}{\rho^{\gamma}}=C・・・(4)\end{align*}

です。

※\(C\)は定数

だから状態1と状態2では、

\begin{align*}\frac{p_{1}}{\rho_{1}^{\gamma}}=\frac{p_{1}}{\rho_{1}^{\gamma}}=C・・・(5)\end{align*}

が成り立ちます。

ベルヌーイの定理を積分する

では(4)式を使ってベルヌーイの定理を積分しましょう。

その前に・・・

ベルヌーイの定理

\begin{align*}\frac{1}{2}v^2 +\int \frac{dp}{\rho}=const・・・(2)\end{align*}

のconstは積分定数を意味しているんですよね。

もともと(2)式を求めるときに、

\begin{align*}vdv+\frac{1}{\rho}dp=0\end{align*}

を積分したのですが、積分定数を用いずに単純に上記の式で「状態1から状態2まで積分する」と考えた方がわかりやすいのですよね（個人的には・・・）

だから、

\begin{align*}\int_{v_{1}}^{v_{2}} vdv+\int _{p_{1}}^{p_{2}}\frac{1}{\rho}dp=0\end{align*}

とすれば、

\begin{align*}\frac{1}{2}v_{2}^2-\frac{1}{2}v_{1}^2 +\int_{p_{1}}^{p_{2}} \frac{dp}{\rho}=０・・・(6)\end{align*}

となります。

(6)式の\(\int_{p_{1}}^{p_{2}} \frac{dp}{\rho}\)を(4)式を使って積分実行すれば良いということになります。

(4)式より\(\rho=\big(\frac{p}{C}\big)^{1/\gamma}\)として、(6)式の積分部分を計算しましょう。

一度試してみてください。（途中計算も書いておきます(‘;’)）

\(\int_{p_{1}}^{p_{2}} \frac{dp}{\rho}=C^{1/\gamma}\int_{p_{1}}^{p_{2}}p^{-1/\gamma}=C^{1/\gamma}\bigg[\frac{\gamma}{\gamma-1}p^{1-1/\gamma}\,\,\bigg]_{p_{1}}^{p_{2}}=C^{1/\gamma}\frac{\gamma}{\gamma-1}\bigg(p_{1}^{1-1/\gamma}-p_{2}^{1-1/\gamma}\,\,\bigg)\)
\(=\frac{\rho_{1}}{p_{1}^{1/\gamma}}\bigg(\frac{\gamma}{\gamma-1}p_{1}^{1-1/\gamma}\,\,\bigg)-\frac{\rho_{2}}{p_{2}^{1/\gamma}}\bigg(\frac{\gamma}{\gamma-1}p_{2}^{1-1/\gamma}\,\,\bigg)=\frac{\gamma}{\gamma-1}\frac{\rho_{1}}{p_{1}}-\frac{\gamma}{\gamma-1}\frac{\rho_{2}}{p_{2}}\)

上で書いたような計算を「わ～っ」てやると・・・・

\begin{align*}\frac{1}{2}v_{1}^2+\frac{\gamma}{\gamma-1}\frac{p_{1}}{\rho_{1}}=\frac{1}{2}v_{2}^2+\frac{\gamma}{\gamma-1}\frac{p_{2}}{\rho_{2}}・・・(☆)\end{align*}

が出てきます!(^^)!

まとめ

ある点での物理量(\(v_{1},p_{1},\rho_{2}\))と別の場所の物理量(\(v_{2},p_{2},\rho_{2}\))で以下の関係式が成り立つ。

\begin{align*}\frac{1}{2}v_{1}^2+\frac{\gamma}{\gamma-1}\frac{p_{1}}{\rho_{1}}=\frac{1}{2}v_{2}^2+\frac{\gamma}{\gamma-1}\frac{p_{2}}{\rho_{2}}・・・(☆)\end{align*}

【仮定】