↓この記事でベルヌーイの定理を導きましたが、本記事はもう少し具体的な例に絞った計算結果を示したいと思います。
この記事で出た結論というのは、
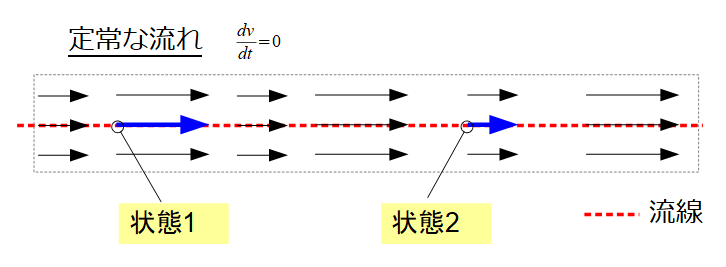
ある点での物理量(\(v_{1},p_{1},\rho_{2}\))と別の場所の物理量(\(v_{2},p_{2},\rho_{2}\))で以下の関係式が成り立つ。
です。
ベルヌーイの定理に当てはめる
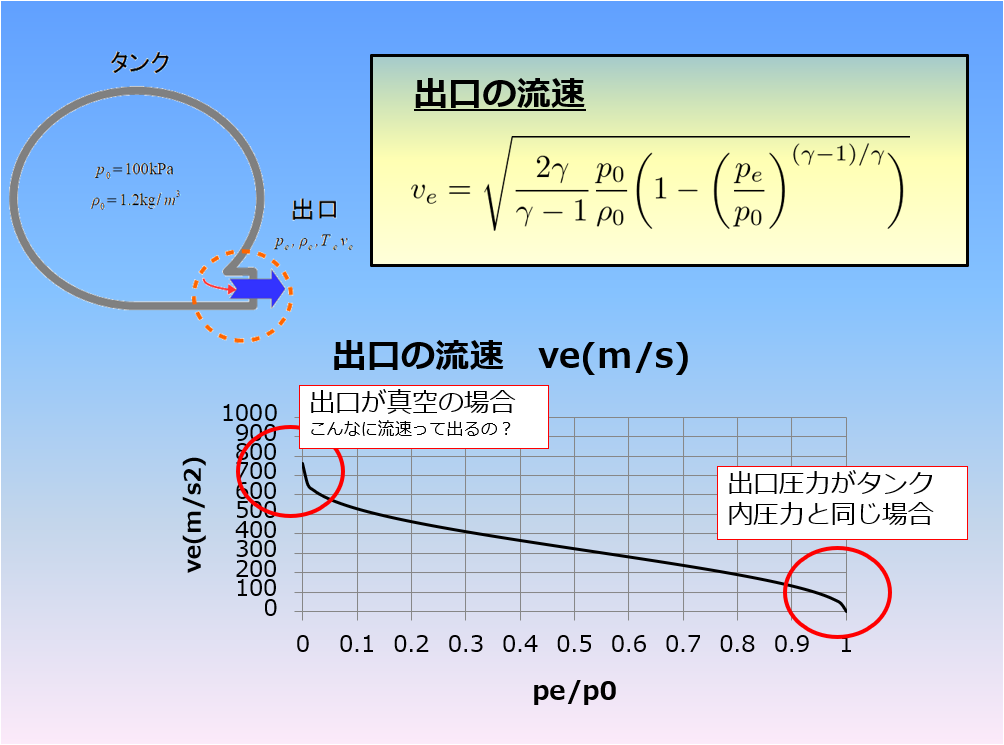
を用いて出口の流速を求めてみましょう。
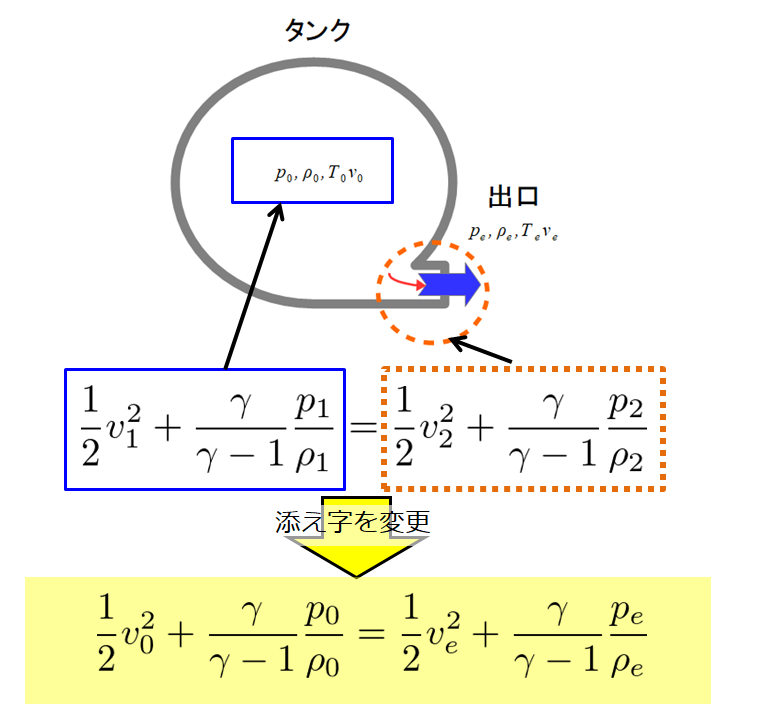

このように絵を見る限り、
と書き換えることができますね。
※タンクの中の気体の物理量には下添え字0を、出口の気体の物理量はexternalの意味で下添え字eを書きます。
タンク内の気体は静止している
ここで、タンクに充満した気体というのは静止しているとします。
静止している解釈でも良いですが、平衡状態になっているためマクロな視点で見た時に状態が落ち着いているという解釈の方が良いでしょう。
なので、タンク内で圧力\(p_{0}\)、温度\(T_{0}\)、密度\(\rho_{0}\)は均一状態であるとみなすことができます。
そう考えると、タンク内の流速は\(v_{0}=0\)と考えてよいことになります。
ゆえに(1)式は第一項が消えることになるので、
となり下記のように出口の流速を求めることができます。
求めることができました。
※タンク内の温度の項が入っていないのに気付きましたでしょうか?
もちろん(3)式は温度\(T_{0}\)を使って書くこともできます。
それは理想気体の状態方程式\(p_{0}=\rho_{0}{R}’T_{0}\)から求めることができます。
\({R}’\):各気体の気体定数 \({R}’=\frac{R}{MW}\)
熱力学的状態としては変数を2つ決めれば、それ以上の変数を使う必要がないので、(3)式に\(T_{0}\)が出てこなかったわけです。
だから\(p_{0},\rho_{0},T_{0}\)のうち2つ変数を選んで(3)式を書くことができるということになります。
具体的な値を入れて流速を計算してみる
タンク内の気体の物理量を以下として考えてみます。
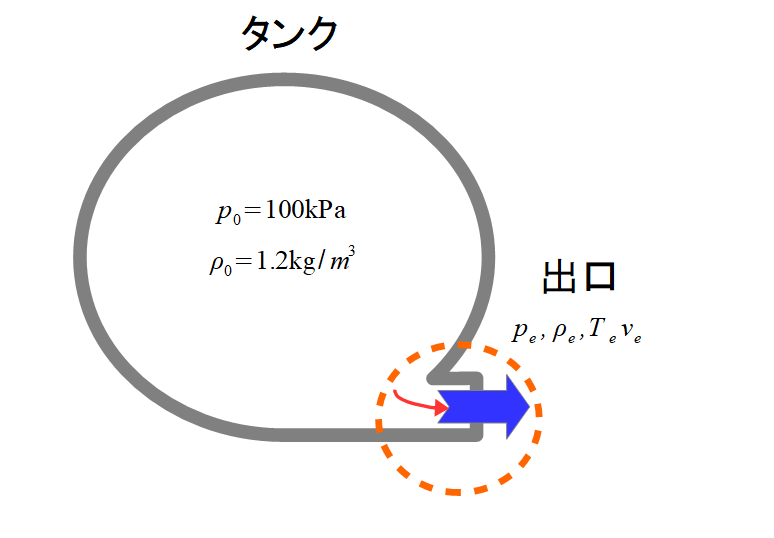

その時の流速はどのようになるでしょうか?
感覚的には出口圧力がタンク内圧力に比べて小さい場合は、圧力差が大きので流速が速くなりそうですよね。
の\(\frac{p_{e}}{p_{0}}\)をパラメータにして流速のグラフを書くと、
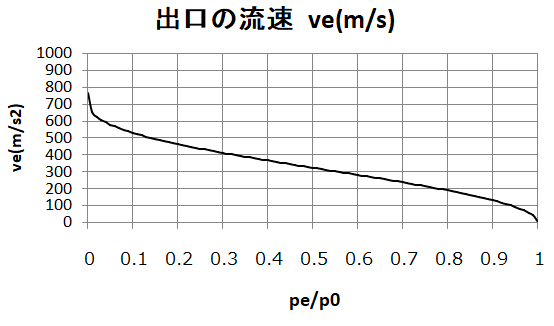

こんな感じです。
計算結果は感覚とあっているか?
上でタンクの出口流速をグラフにしてみましたがこれが感覚と合っているのか考えたいと思います。
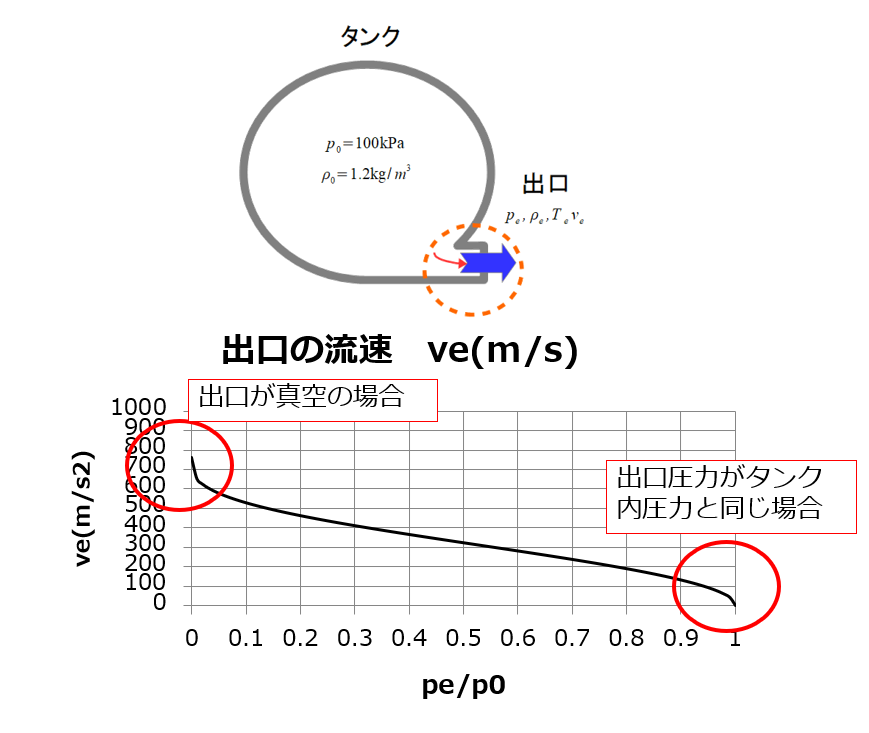

出口圧力がタンク圧力と同じ場合
この場合は圧力差がないために流速が0となりますよね。
つまり出口の周辺気体も含めてタンクの状態と同じであるために、平衡状態となっているため流速は発生しません。
もし、出口付近の圧力がある値であれば熱力学で考えると、エントロピー増大に向かって別の平衡状態になろうとして流速が発生します。(そのような場合は非平衡状態になっているため、熱力学が成り立たないんのではないかと思うかもしれませんがこの場合にも熱力学が成り立つ場合が多いです。問題なのは非平衡だから熱力学が成り立たないとかということではなく、平衡状態から別の平衡状態への時間間隔が長いかどうかってことです。何に対して長いかというのはありますが・・・・・熱力学はたとえ間に非平衡な状態を挟んでも、平衡状態と平衡状態をつなげてみると熱力学の学問が十分成り立つと考えても良いでしょう)
出口が真空である場合
この場合はもっとも圧力差が大きいので流速が速くなりそうです。
実際にグラフを見るともっとも流速が速くなっているのが見られます。
その速度は「なんと約750m/s!!」
こんなに流速が出るものなのでしょうか?
答えはよく教科書で書いてある通り「出口での流速は音速が最大」となります。
それが臨界状態となります。
まとめ
タンクからの出口速度を求めてみました。



計算結果