物理現象を数理モデルで扱うにあたっては絶対にテーラー展開は覚えておかなくてはいけません。ここでは、テーラー展開の数学的な証明は説明は省き要点だけ書きます。
テーラー展開
$x=a$のまわりでの関数の形を知りたい場合、テーラー展開を使います。
テーラー展開は、
と書くことができます。
Σの和があるとわかりにくいですが、展開しておくと多項式近似であることがわかります。
&+\frac{f^{(2)}(x)}{2!}|_{x=a}(x-a)^{2}\\
&+\cdot\cdot\cdot+\frac{f^{(n)}(x)}{n!}(x-a)^{n}+\\
&\cdot\cdot\cdot\end{align*}
※\(f^{(n)}(x)=\frac{d^{n}f(x)}{dx^{n}}\)：n階微分
念のため注意ですが$\frac{f^{(1)}(x)}{1!}|_{x=a}$は$x$で微分してから$x=a$を代入するって意味です。
$x=a$を代入してから微分してはいけませんよ（0にしかなりませんから）。
それでは具体例を見てみましょう。
どういうときに使うのかを簡単な例で示したいと思います。
具体例1：関数を簡単にする
例えば、$y=\sin x$という関数を考えて「$\sin$のままだと扱いにくいな～。$x=0$のまわりだけ情報がほしいな～」ってなったとします。
それでよく見ると$y=x$とかで近似できそうであることがわかります。
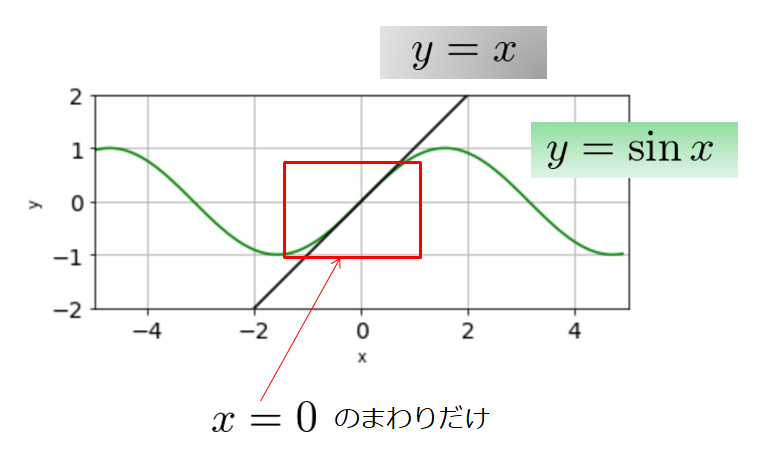
だから、$y=\sin x$は$x=0$のまわりだけ見たら$y=x$と見ても良いということになります。
$y=\sin x$よりは$y=x$の方が扱いやすいですよね。
$y=\sin x$はそれほど扱いにくい関数ではありませんが、複雑な関数やそもそも関数の形がよくわからない場合にはテーラー展開は有効に使うことができます。
正確には$x=0$のまわりで近似するのはマクローリン展開と言います。
テーラー展開は$x=0$のまわりに限った話ではなく、任意の$x$のまわりでの話です。
具体例2：関数の形が良くわからない場合（ポテンシャルの極小値まわりの近似）
例えば、粒子間の相互作用を考えることにします。
でも粒子間の相互作用なんて具体的な形はよくわからない・・・・どうしよう。
とりあえず適当に「ポテンシャル$U(x)$」として考えるかとなったとしましょう。
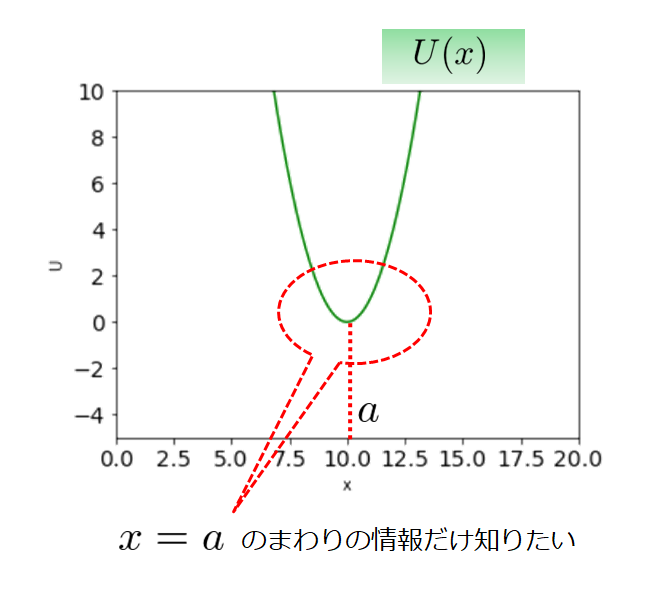
ある粒子に対して考えると何か位置によるポテンシャルというのが存在することになります。
これは、例えば上のグラフで考えると、$x=a$ではポテンシャルエネルギーが低いですけど、$x$が大きい位置や小さい位置に粒子が移動しようものならたちまちポテンシャルエネルギーが大きくなってしまいます。
エネルギーは最小出る方が「系として居心地が良い」のですよね。
（上の絵を見ても・・・・なんか最小値の方がおさまりが良くて居心地良さそうですよね・・・・そう見えませんかね(笑)）
それはそうと、全ての$x$に対して$U(x)$の関数の振る舞いを知りたいのではなくて、実は\(x=a\)のまわりでの\(U(x)\)の関数の振る舞いを知れれば十分だということになります。
ということは$x=a$のまわりでテーラー展開をしましょう。
となりました。
ここで、$x=a$のまわりでの展開であるので、$x-a$は0に近い値であるということになります。だから、高次の項は「小さい値をさらに何乗かする」ことになるのでとても小さい値になっているわけです。(2)式は無限に和を続けることに意味がなく第2項まで残しておきます。
そうすると、(2)式を2次の項まで残して、
となります。
$U(a)$や$\frac{U^{(2)}(x)}{2!}|_{x=a}$は単なる定数ですし$\frac{f^{(1)}(x)}{1!}|_{x=a}$に至ってはそもそも\(x=a\)で極小値をとっているような関数を想定しているので0のはずです。
ということは、
ってことになります。
全然よくわからなかった関数がテーラー展開をさせることで空間的には$x=a$という限定的ではありますが、ずいぶんと簡単な形にできました。
具体例3：微分の離散化に使う
テーラー展開は微分の離散化などにも使われます。
微分の離散化とは大きなくくりで言うと数値計算での離散化のことを指しています。
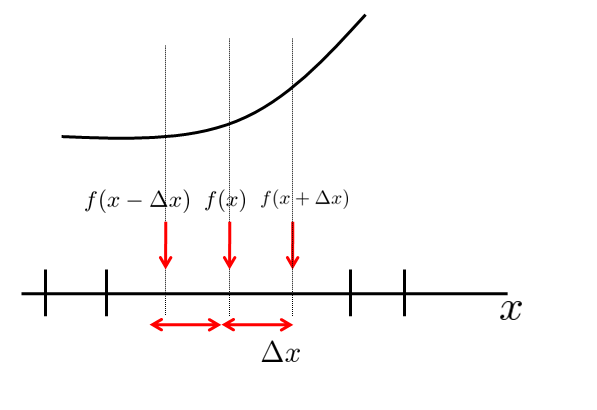
例えばこのように$f(x)$とい関数があるのですが、数値計算を行う際はPCが処理するには代数的な値として入力する必要があるために微分などは扱うことはできません。
なので、どうにかして微分を代数的に表現しなくてはいけません。
そこでテーラー展開を使います。
例えば、\(f(x+\Delta x)\)と\(f(x-\Delta x)\)とを1次の項までテーラー展開してみます。
そうすると次の２つの有名な離散化手法が導けます。
前進差分
(5)より、
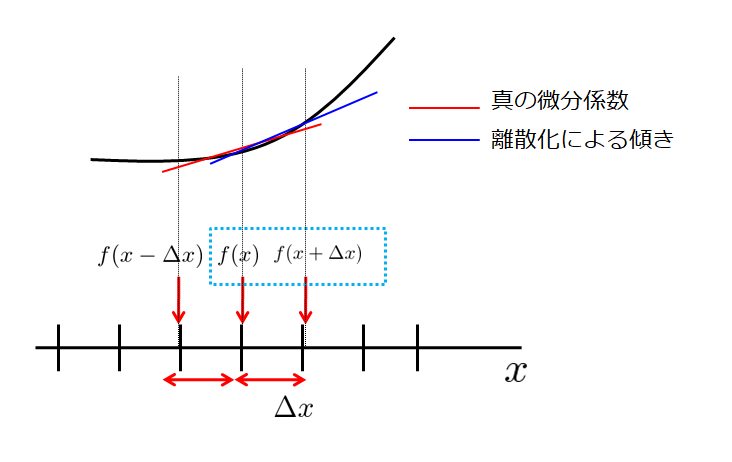
これは求めたい位置\(x\)での微分に対して、前の値\(x+\Delta\)の値を使って微分を表現するので前進差分といいます。
実際求めたい（真の）微分係数と比較すると、少々のずれがありますね。
これが離散化による誤差であることを意識しておいてください。
後退差分
(6)より、
これは求めたい位置\(x\)での微分に対して、後ろの値\(x-\Delta x\)の値を使って微分を表現するので後進差分といいます。
前進差分と同様に実際求めたい（真の）微分係数と比較すると、少々のずれがありますね。
これが離散化による誤差であることを意識しておいてください。
中心差分
前進差分と後進差分より一般的に精度が良いと考えられている中心差分も示しておきます。
これにはまず$f(x+\Delta x)$と$f(x-\Delta x)$を2次の項までテーラー展開してみます。
(9)式と(10)式を足せば、中心差分の完成です。
精度が良いというのは、テーラー展開の次数が多いからそのように考えられています。
（2次までテーラー展開をしているので、2次の精度と言ったりします。）
中心差分の場合は、前進差分・後進差分よりは（真の）微分係数に近いですね。
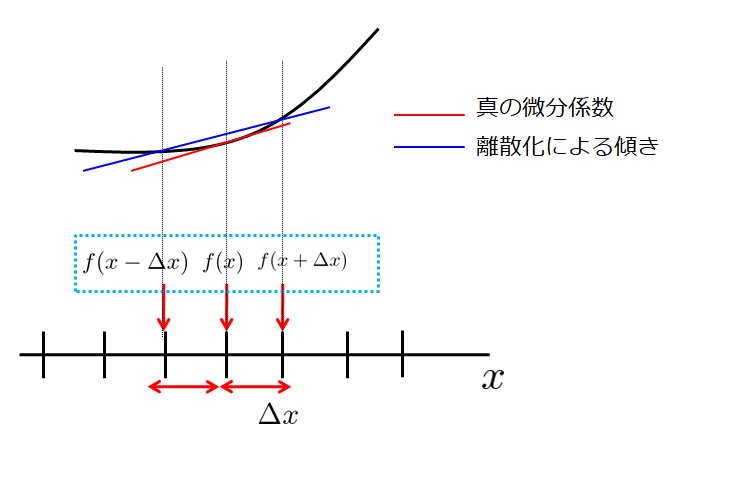
それゆえに精度がテーラー展開の1次近似(前進差分・後進差分）よりは良いということです。
しかし、必ず精度が良くなるのかどうかは保証できません。
精度の良しあしは解きたい偏微分方程式にもよります。（移流方程式などの中心差分は解が振動するなどあるそうなので、よく自分で使いたい離散化手法を見極めないといけないです。）
1次元の移流方程式を今回紹介した「前進差分、後退差分、中心差分」で数値計算した記事を書きました。解の安定性などコードを書きながら学べますのでご参考ください。
本日は以上です(‘ω’)
Follow @t_kun_kamakiri