流体力学ヘルムホルツの渦定理【渦ができる要因を理解する】

前回は、流体力学にケルビンの循環定理というものを示しました。

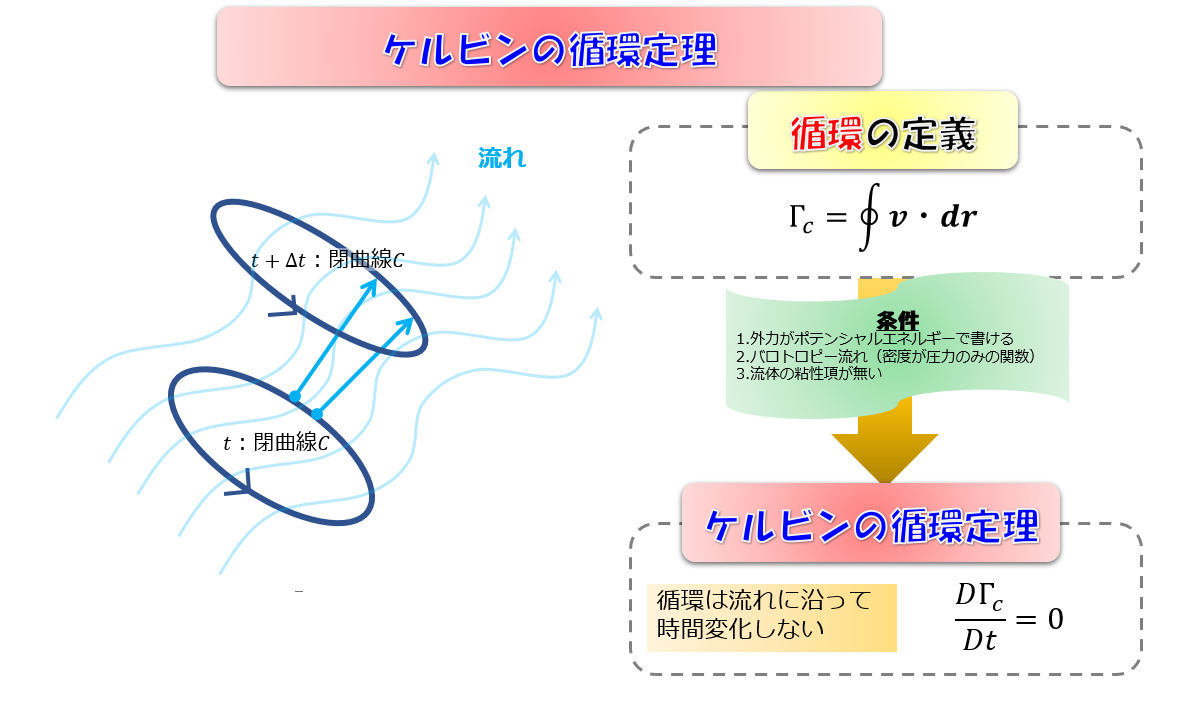
復習　ケルビンの循環定理とは何か？

まずはケルビンの循環定理の復習を行います。

前回の記事はこちら

流体力学：ケルビンの循環定理【渦ができる要因を理解する】

ケルビンの循環定理

記の3つの条件を課すと、「流れに沿って変化する循環の時間変化を考えると、循環は変化しない」。

条件

外力がポテンシャルエネルギーで書ける\(\boldsymbol{K}=-\nabla U\)
バロトロピー流れ（密度が圧力のみの関数)\(\rho=f(p)\)
流体の粘性項が無い

循環が変化しない（保存）

\begin{align*}
\frac{D\Gamma_{c}}{Dt}=0
\end{align*}

ここから重要な結論を導くことができます。

渦度はその名の通り渦を定義する一つの物量であります。

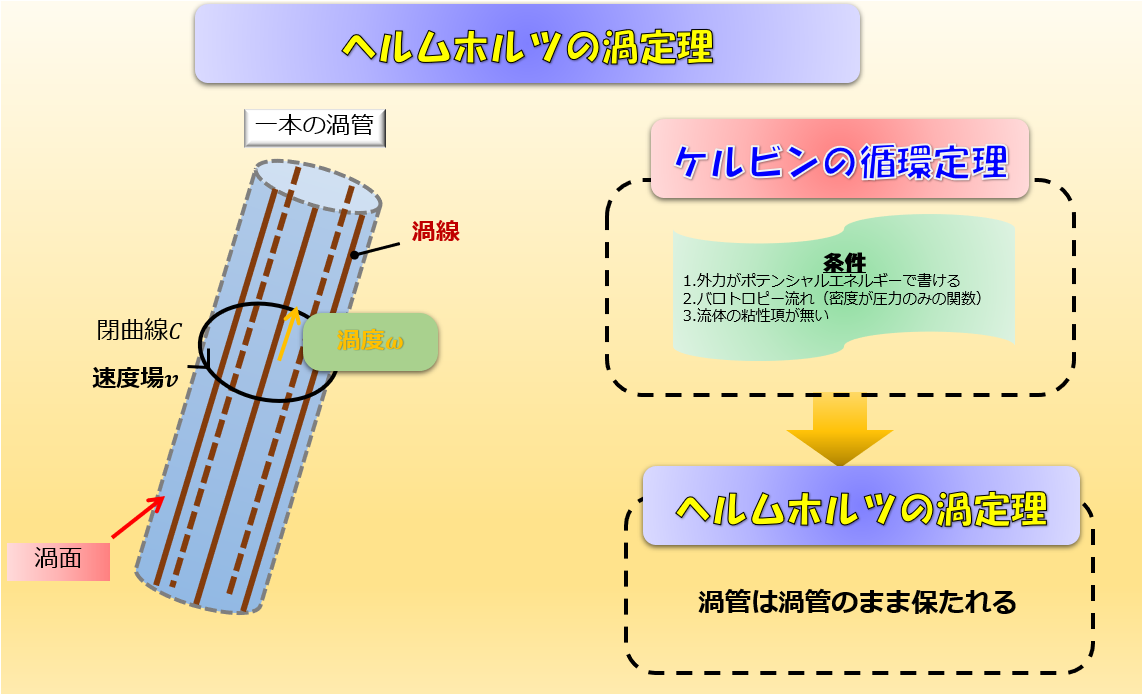
循環は下記の絵のように渦度に関係する量です。

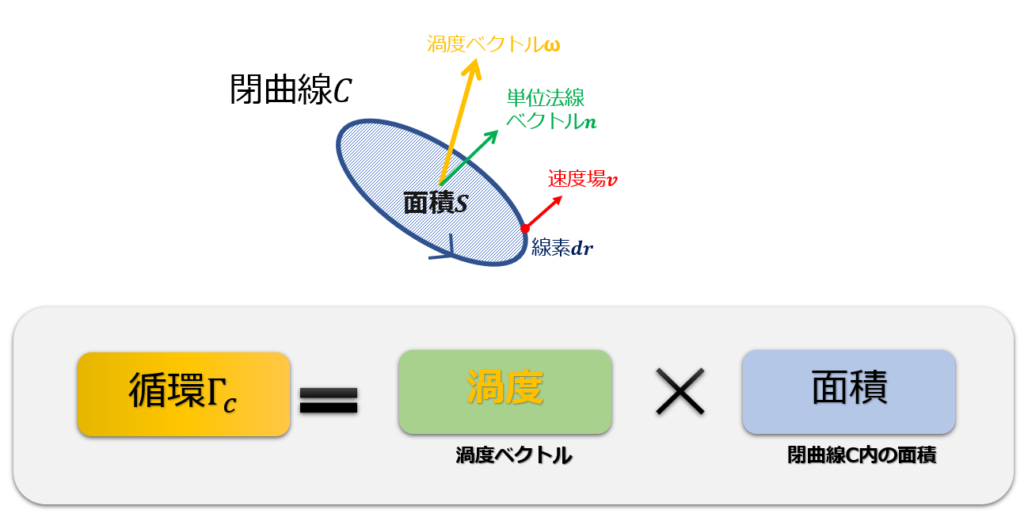
その循環が、下記の3つの条件を課すと、時間変化しないということをケルビンの循環定理が教えてくれます。

条件

外力がポテンシャルエネルギーで書ける\(\boldsymbol{K}=-\nabla U\)
バロトロピー流れ（密度が圧力のみの関数)\(\rho=f(p)\)
流体の粘性項が無い

ということは、

循環が０・・・・つまり渦度が０・・・・渦がない状態から始まったら上記の条件のもとでの流れであると、ケルビンの循環定理より循環はず～っと０である、

つまり渦はどう頑張っても生成できないということを教えてくれています。

確かに上記の3つの条件を課すことは実現象ではあまりに限定され過ぎた流れでしょう。

ならば、上記のような条件を課さなければケルビンの循環定理は成り立たないということになります。

言い換えると、上記の3つの条件のうちのどれかでも崩れると、渦を生成しても良いという結論になります。

まとめると、ケルビンの循環定理が成り立つならば・・・

渦なし\(\omega=0\)→ずっと渦なし
渦あり\(\omega \neq =0\)→ずっと渦あり

渦管を考える

ヘルムホルツの渦定理を説明しする前に、渦管について考えてみます。

渦管とは何かというと、

渦線：渦度ベクトルを流線のようにつなげた曲線
渦管：流れの中のある閉曲線上の各点を通る渦線
渦糸：渦管を断面積を無限小にしたもの

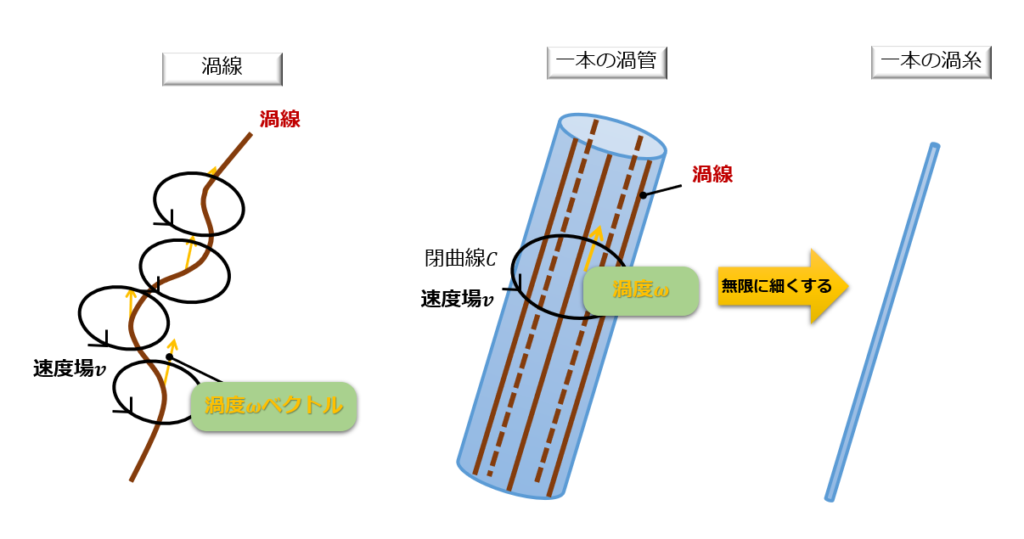
今回は上の渦管について考えていきます。

循環は渦管に固有の量

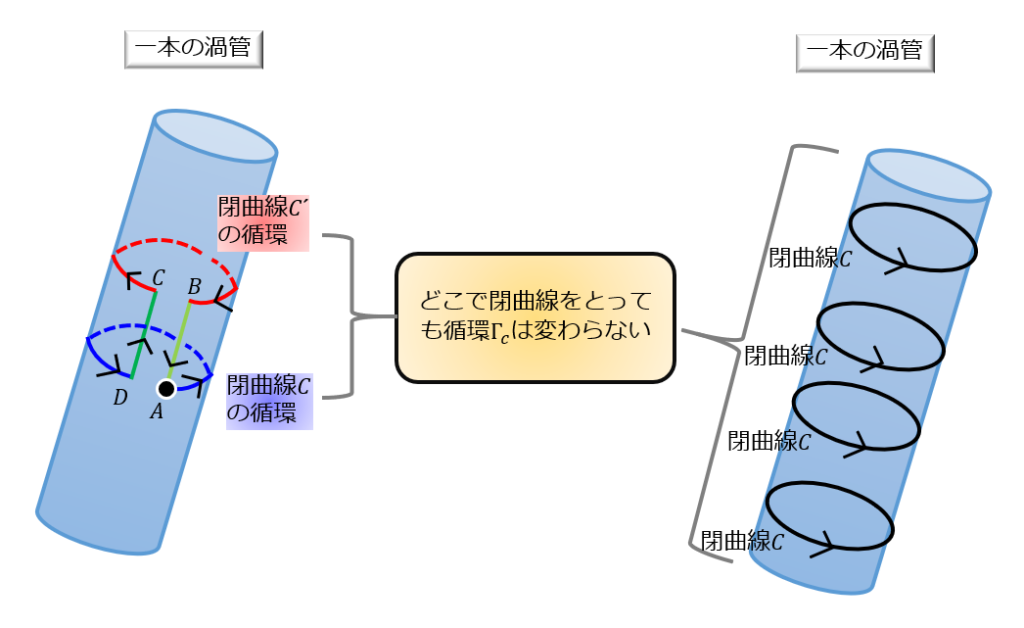
下記のように1本の渦管を考えるとき、渦管の側面に沿って1周する閉曲線がつくる循環は、

渦管固有の量になる
循環は閉曲線\(C\)の取り方に依らない

要するに、渦管のどの部分の閉曲線をとって循環を計算しても同じだよということを示すことができます。

下記の絵のように、渦管を考えます。

その渦管の側面に沿って閉曲線\(C\)と閉曲線\(C^{‘}\)、それからそれをつなぐ点\(A,B,C,D\)を用意します。

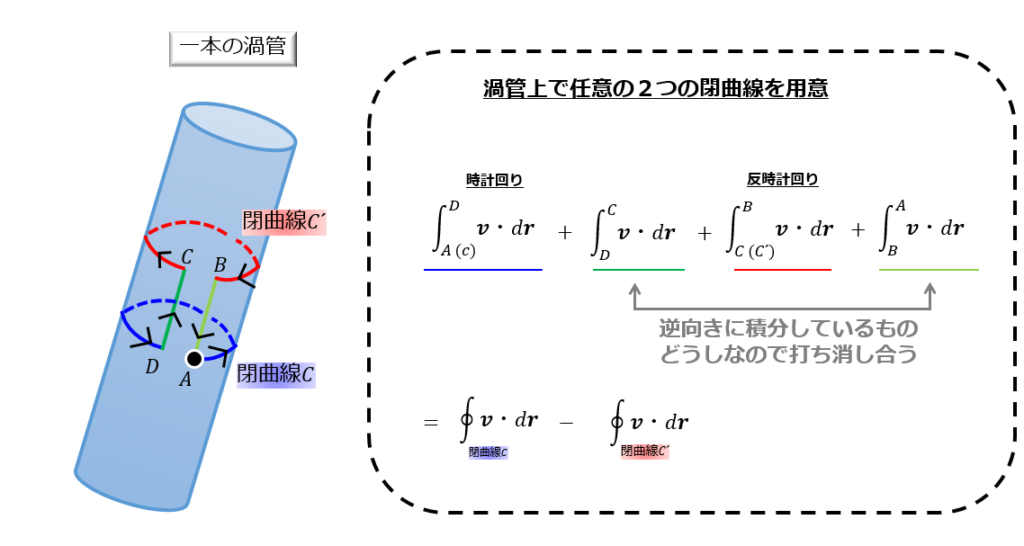
※「\(A\)と\(D\)」「\(B\)と\(C\)」はほぼくっついている状態と思ってください。

この絵のように、

閉曲線\(C\)で線積分
\(D\)から\(C\)で線積分
閉曲線\(C^{‘}\)で線積分
\(B\)から\(A\)で線積分

この流れで線積分を実行していくと、最終的に1周して元の位置に戻ってきますので、同じ値同士を引き算していることになります。

よって、

\begin{align*}
\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}-\oint_{c^{‘}} \boldsymbol{v} \cdot d\boldsymbol{r}=0
\end{align*}

つまり、

\begin{align*}
\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=\oint_{c^{‘}} \boldsymbol{v} \cdot d\boldsymbol{r}\tag{1}
\end{align*}

となります。

これは、渦管上で適当に選んだ2つの循環が同じであるということを意味しています。

渦管固有の量になる
循環は閉曲線\(C\)の取り方に依らない

ということです。

※これはケルビンの循環定理が成り立つかどうかに関わらず、一般的な結論であることに注意してください。

ヘルムホルツの渦定理

では、ヘルムホルツの渦定理をみていきます。

まず、考え方をわかりやすくするために、渦面というのを考えます。

カマキリ

渦面とはなんだ

渦線、渦管、渦糸、渦面と用語が多いですが(;’∀’)

渦面

渦面というのは渦線に沿って貼られる曲面というものです。

絵を描いてみましょう。

先ほどは一本の渦管のまわりで閉曲線を書きましたが、複数の渦管のまわりに閉曲線を作った状態を考えます。

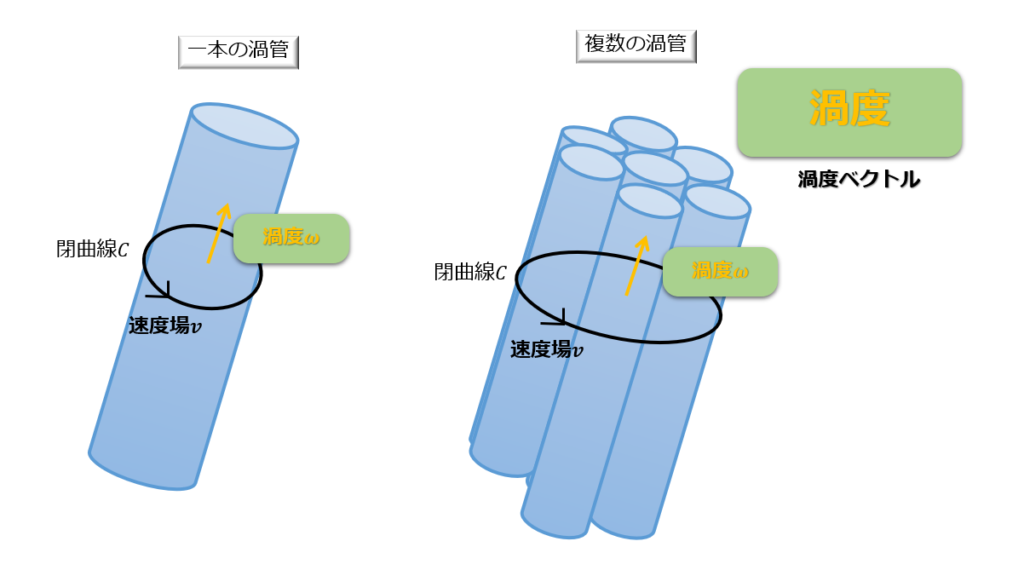
そこで、適当な曲線を引いて、その曲線上の各点に通る渦線が作る面を考えます。

それが渦面です。

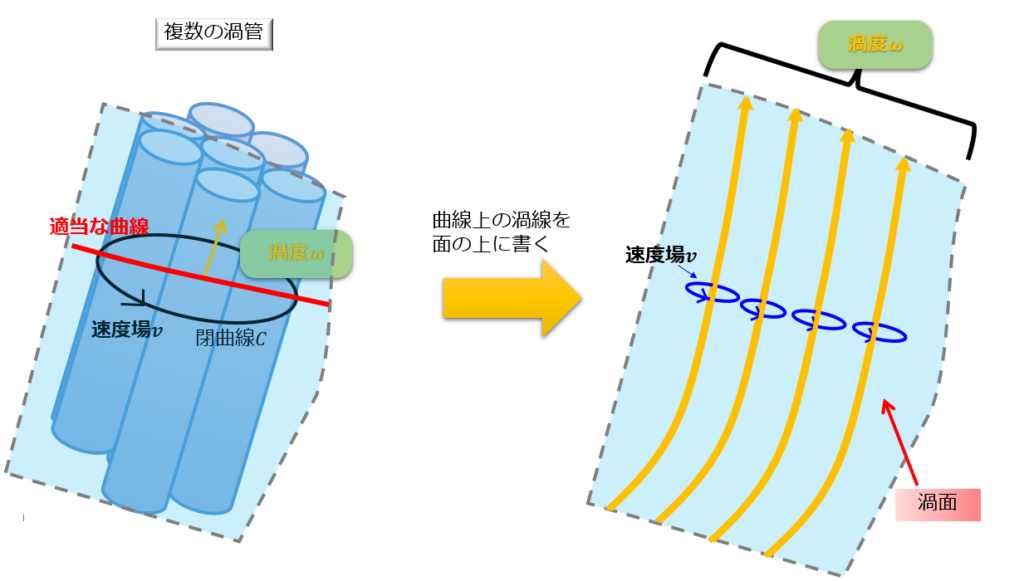
流れに沿って渦面は渦面として保たれる（渦面上で循環0）

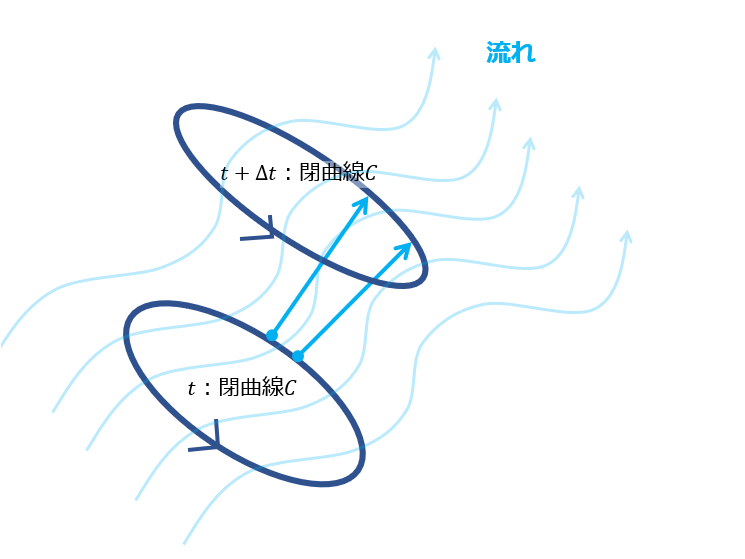
渦面上で流れに沿って渦面は渦面として保たれるというのを示すことができます。

それは、下記の絵のように渦面上に適当に閉曲線を描きます。

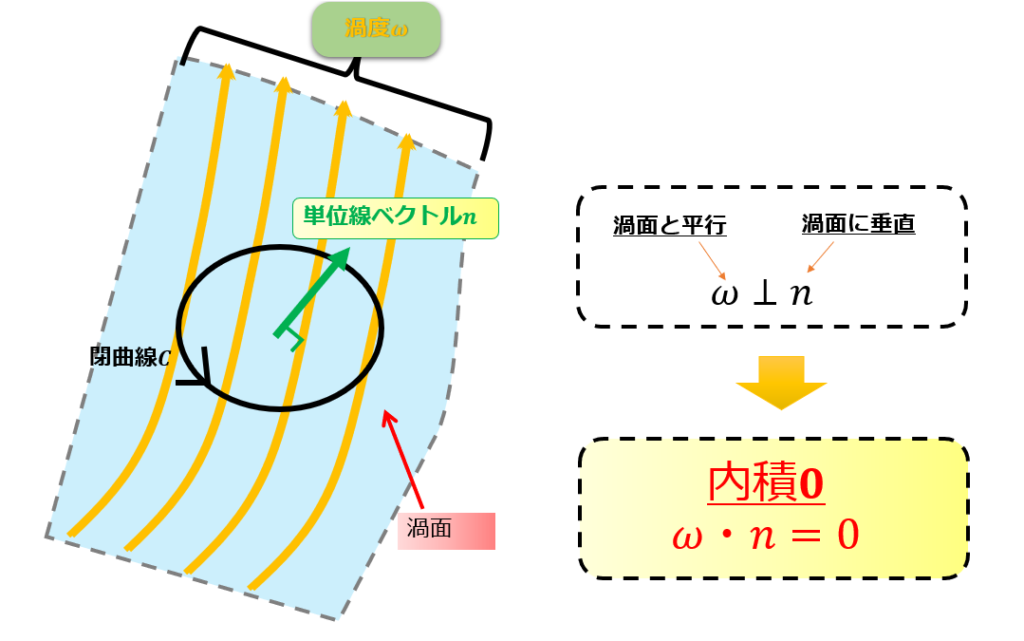
当然、渦面上で閉曲線を描くと、閉曲線との法線ベクトル\(\boldsymbol{n}\)は渦度\(\boldsymbol{\omega}\)と垂直であるので、内積が0になります。

\begin{align*}
\boldsymbol{\omega}\cdot \boldsymbol{n}=0\tag{2}
\end{align*}

ということは、この渦面上での循環は、

\begin{align*}
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=\iint_{S}\bigg(\nabla\times \boldsymbol{v} \bigg)\cdot\boldsymbol{n}dS=\iint_{S}\boldsymbol{\omega}\cdot\boldsymbol{n}dS=0\tag{3}
\end{align*}

これを見ると渦面は循環が０ということになるので、ケルビンの循環定理より「渦面は渦面のとしてずっと変わらない（保たれる）」ということになります。

くどいようですが、ケルビンの循環定理はどんな時でも成り立つというものではなく、下記の条件のときに定理であることを再確認しておきましょう。

条件

外力がポテンシャルエネルギーで書ける\(\boldsymbol{K}=-\nabla U\)
バロトロピー流れ（密度が圧力のみの関数)\(\rho=f(p)\)
流体の粘性項が無い

渦管もひとつの渦面ですよね。

こんな感じで渦面をグルっと巻いて渦管を作ります。

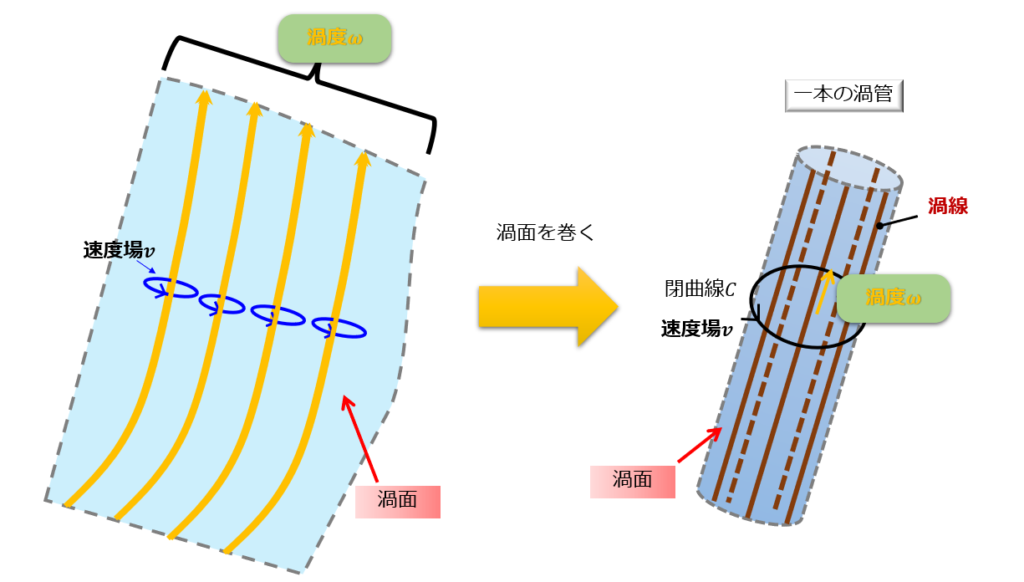
このようにすると、ケルビンの循環定理より、

「渦面は渦面のとしてずっと変わらない（保たれる）」→「渦管は渦管のままずっと変わらない（保たれる）」

ということになります。

そして今まで議論した内容をまとめると・・・・

渦管固有の量になる
循環は閉曲線\(C\)の取り方に依らない
渦管は渦管のまま保たれる

です。

これを簡潔に言い換えると、

「循環は渦管に固有の量であり、ぞの渦管は保たれる」ということになります。
これが、ヘルムホルツの渦定理と呼ばれるものです。
※ただし、上の結論はケルビンの循環定理が成り立つ条件下であることに注意。

まとめ

渦管のどの部分の閉曲線をとって循環を計算しても同じ
ヘルムホルツの渦定理：循環は渦管に固有の量であり、ぞの渦管は保たれる

※ただし、ヘルムホルツの渦定理はケルビンの循環定理が成り立つ条件下であることに注意。

補足：一本の渦糸について

ここでは一本の渦管について考えます。

「一本の渦管を無限に細くしていったものを渦糸という」という説明は上でしました。

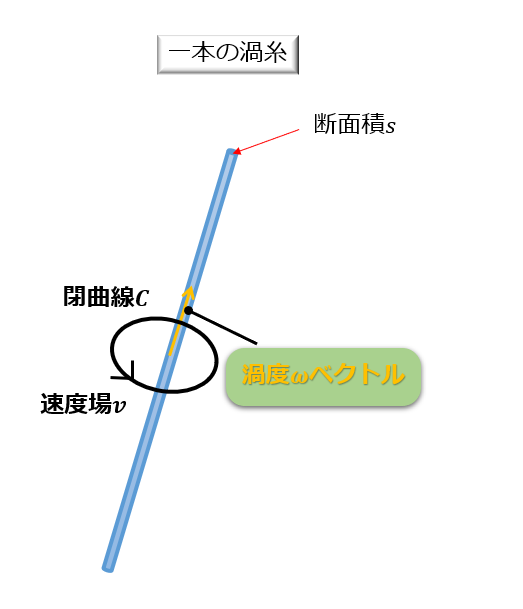
この渦糸の細さ（断面積)を\(s\)というふうに書くことにします。

さらに、渦管の断面積出の渦度はどこも変わらない(常に一定値\(omega\)）と単純化して考えると、循環は、

\begin{align*}
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=\iint_{S}\bigg(\nabla\times \boldsymbol{v} \bigg)\cdot\boldsymbol{n}dS=\boldsymbol{\omega}\iint_{S}\cdot\boldsymbol{n}dS=\boldsymbol{\omega}s\tag{4}
\end{align*}

補足：渦線は「境界から境界へ伸びる」か「渦輪を作るか」しかない

上で解説した渦管のどの部分の閉曲線をとって循環を計算しても同じというのは、渦管（渦管の側面である渦線）上のどこをとっても循環が同じっていうことですよね。

では、どこまでも渦管の循環は同じなのかというと・・・・そういうわけではなく、下記の2つに限られるということになります。

１．渦管が無限に続くか、境界から境界まで伸びる

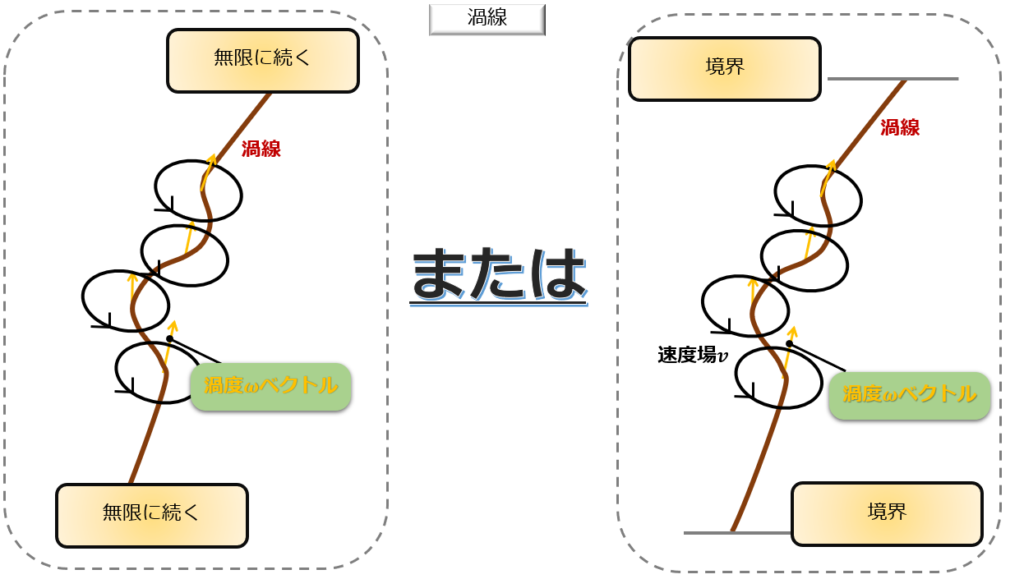
無限に伸びるというのは現実的ではないので、渦線が切れることなく境界から境界まで伸びるというイメージになります。

２．自分自身で閉じてしまって渦輪をつくる

補足については以上です。

カマキリ

渦は奥深い

流体力学を深く理解するための参考書

初心者から中級者で流体力学を学ぶのにおすすめの参考書を以下に列挙しておきます。
流体力学は、「工学向け」か「理学向け」で内容が結構変わってきます。

工学部向け流体力学

工学向けでは以下の3冊をお勧めします。

流体力学 (JSMEテキストシリーズ)

日本機械学会

3,240円(11/20 18:37時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

👆こちらは、初心者でもわかりやすく理解できると思います。

演習書としては以下のものが、難しすぎず・・・がっつり練習できます。

演習で学ぶ「流体の力学」入門第2版

孝夫, 西海, 隆義, 一柳

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

工学部であれば圧縮性の流体まで、学ぶことが多いと思いますので、「圧縮性流体」の参考書としては以下の書籍がお勧めです。

圧縮性流体力学―内部流れの理論と解析

松尾一泰

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

理学部向け流体力学

僕は、理学部出身なので主に愛用していた書籍を紹介します。

流体力学 (前編) (物理学選書 (14))

今井功

7,480円(11/21 11:23時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

👆こちらの書籍は流体力学を学ぶために一番最初に購入した本なのですが、今まで読んだ流体力学の中で一番わかりやすいと思っています。
ただ、残念過ぎるのは「前編」だけを書いて著者がお亡くなったため、「後編」がないという参考書です。それなのに絶版にならずに書籍で見かけるんですから、相当有名なんだろうなと思います。

もう少し優しい参考書としては「今井氏」の流体力学がお勧めですね。