こんにちは(@t_kun_kamakiri)。
さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知りたくとお読みいただいていることかもしれません。
「楕円の面積」や「楕円体の体積」の公式を求め方を紹介
結果をもったいぶらないで、以下にまとめておきました。

ついでに、色々な導出方法があるので読むだけで楽しいと思いますよ(^^)/
理解のためのステップ
下記のステップを踏んで「4.楕円体の体積」を求めたいと思います。
- 円の面積
- 楕円の面積
- 球の体積
- 楕円体の体積
楕円の体積だけではなくて「円の面積」や「楕円の面積」なども一度計算しておくと、楕円の体積は決して忘れることはありません。
以下の複数の解法を学びながら、楕円の体積の求め方までたどり着いてみてください(^^)v
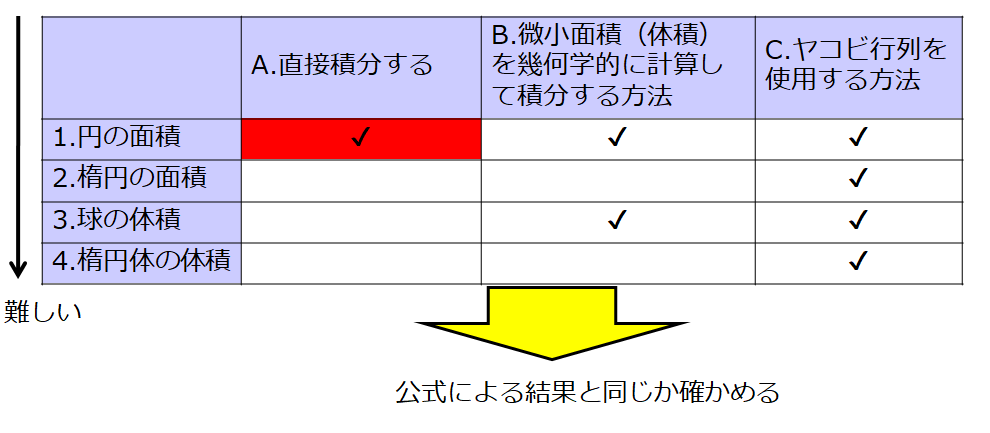
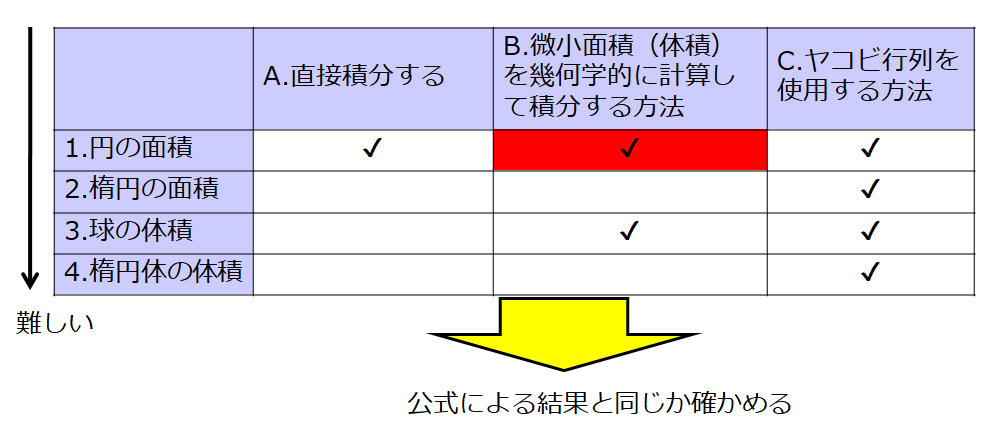
A.直接積分する
B.微小面積(体積)を幾何学的に計算して積分する方法
C.ヤコビ行列を使用する方法
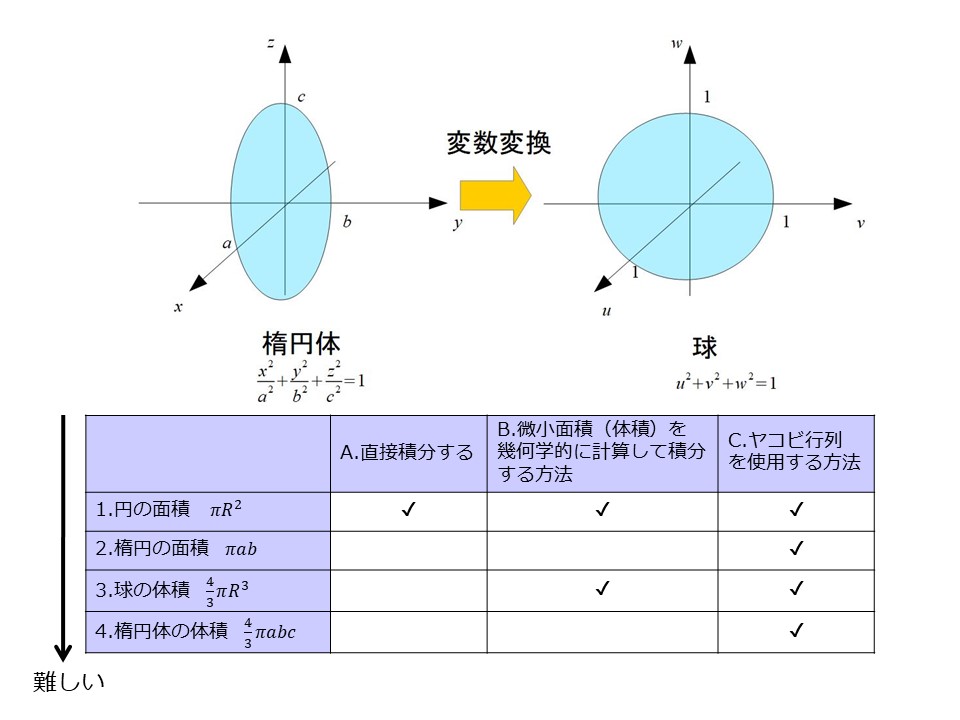
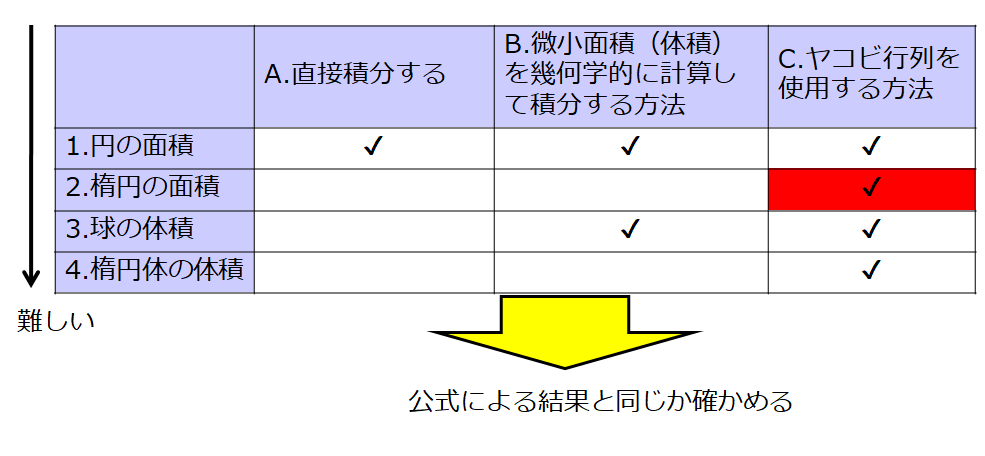
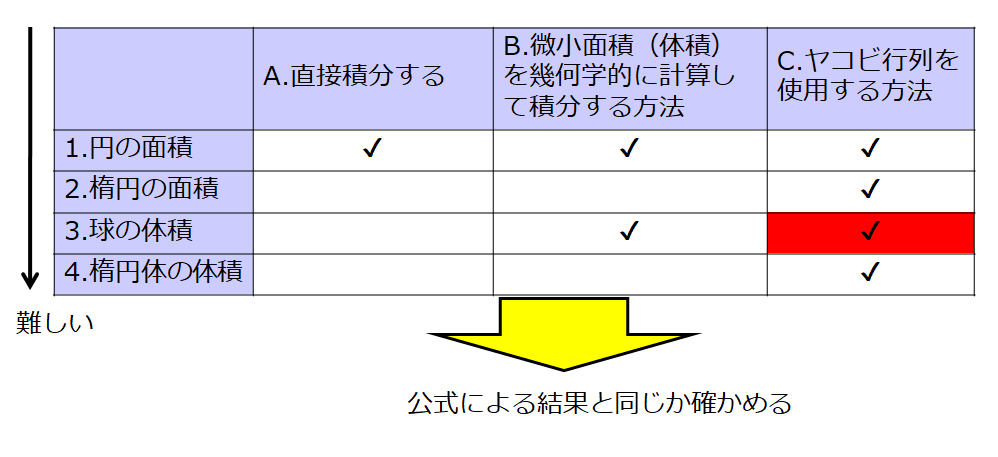
では、表にまとめてみましょう。
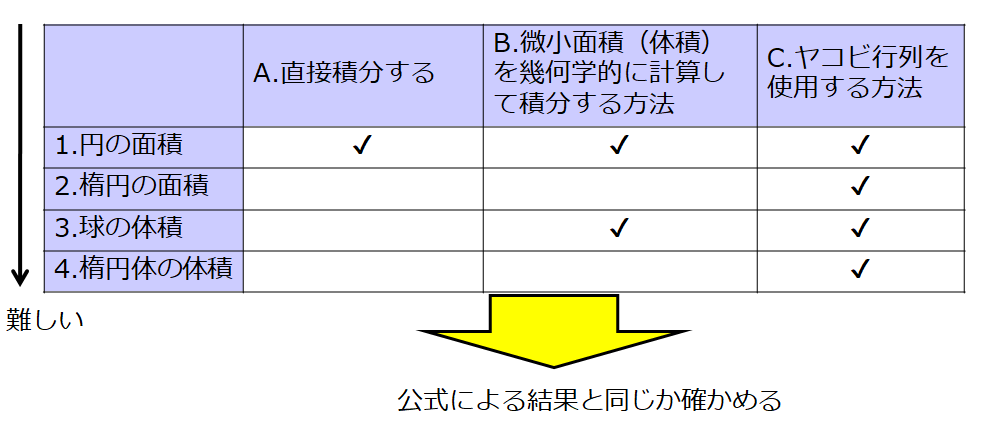

チェックを入れた方法(AとBとCの方法)で計算して、公式と一致しているかどうかを確認しようと思います。
ここでは、「(1-B)について説明する」と書けば、「1.円の面積」を「B.微小面積(体積)を幾何学的に計算して積分する方法」で計算する方法を説明すると理解してください。
円の面積
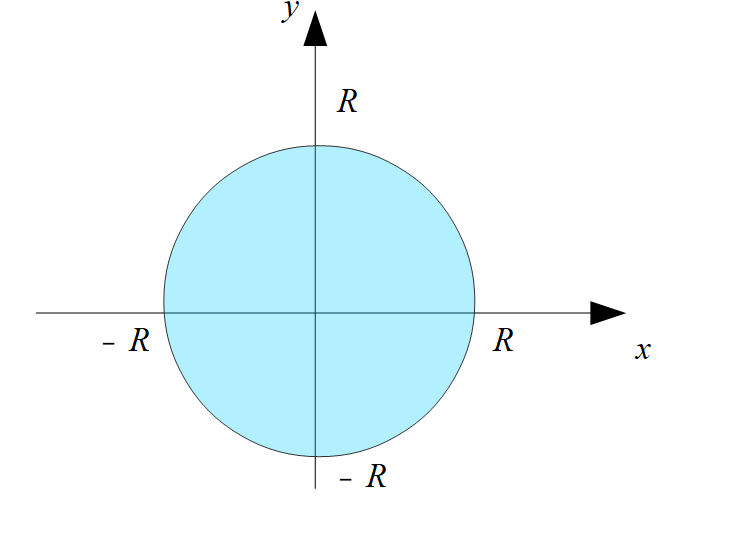

\(x^2+y^2=R^2\)の内部の面積を求めることになります。
つまり、
\(x^2+y^2 \leq R^2\)である領域の面積を求める。
変数\(x,y\)の領域は、
\(-R \leq x \leq R\)
\(-R \leq y \leq R\)
です。
(1-A)直接的な解法

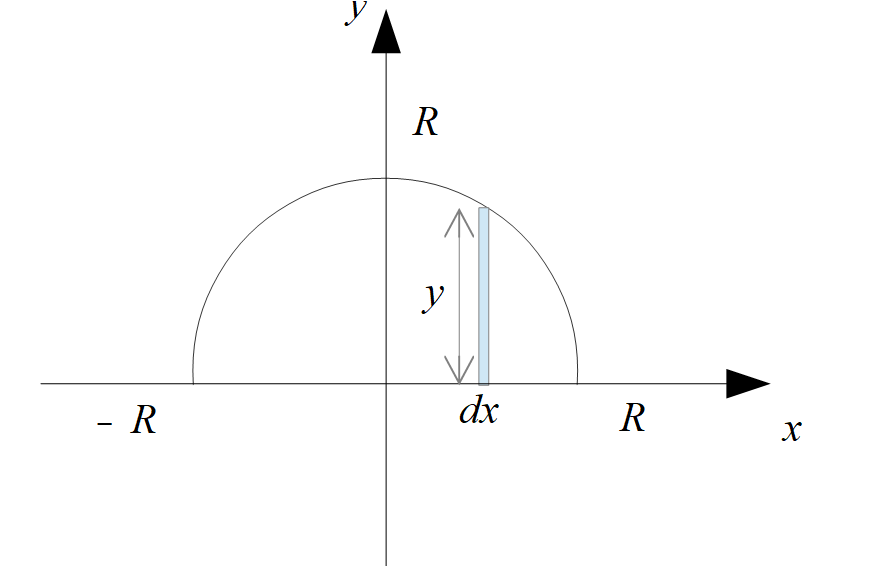
上記の(1-A)をやっていくことになります。
まず、求めたい円の面積を\(S\)とします。
直接的な方法というのは、円の方程式\(x^2+y^2=R^2\)を関数として扱って、下記の図の微小面積を\(x\)について足し合わせることを意味しています。

ここで注意しなければならないのが、「円の方程式」とは言っても「円の関数」とは言わないということです。
関数とは「xの値をひとつ決めるとyの値がただいひとつに決まる」ものです(そのように中学生の時に習いました)。
円の方程式は、「xの値をひとつ決めるとyの値が2つ存在することになる」ので関数とは言えません。
確かに、
y=\pm\sqrt{R^2-x^2}\cdot\cdot\cdot (2)\end{align*}
とするとある\(x\)の値に対して\(y\)の値が2つ出てきます。
これでは積分が実行できないので、+記号だけ使います。
y=\sqrt{R^2-x^2}\cdot\cdot\cdot (3)\end{align*}
そうすると関数として扱うことができるので積分が実行できます。
求める面積は図のように上半分の面積を求めて2倍すれば良いことになります。
S=2\int_{-R}^{R} \sqrt{R^2-x^2} dx \cdot\cdot\cdot (4)\end{align*}
さてこれを実行すれば良いのですが、ルートが存在すると積分できないので、置換積分しましょう。(変数を置き換えることになります)
例えば、この場合であると、
x=R\sin\theta\cdot\cdot\cdot (5)\end{align*}
と置くと、良いです。
まず\(dx\)を求めます。
(5)式を使って、
\frac{dx}{d\theta}=R\cos\theta\end{align*}
となるので、
dx=R\cos\theta d\theta\cdot\cdot\cdot (6)\end{align*}
と決まります。
次に・・・・
\sqrt{R^2-x^2} =R\sqrt{1-\sin^2\theta}=R\cos\theta\cdot\cdot\cdot (6)\end{align*}
となります。
さらに・・・
積分区間は$x$から\(\theta\)に変わります。
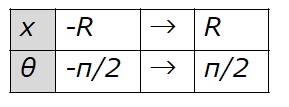
よって、(4)式は、
S=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}R^2\cos^2\theta\, d\theta\cdot\cdot\cdot (7)\end{align*}
となりますので、これを求めれば良いことになります。
半角の公式\(\cos^2\theta=\frac{1+\cos2\theta}{2}\)を使えば、(7)式は、
S=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}R^2\cos^2\theta \,d\theta=2R^2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1+\cos2\theta}{2}\, d\theta=2R^2\bigg[\frac{\theta}{2}+\frac{1}{4}\sin2\theta\bigg]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}=\pi R^2\cdot\cdot\cdot(8)\end{align*}
となります。
よって、公式通りになります。
複雑な関数や3次元の体積を求める方法の基本的な積分はこのような手法であると思います。
しかし、何もかもデカルト座標\((x,y,z)\)として積分を実行することが賢いやり方だとは思わないので、場合によっては別の座標系に置き換えたりして上手く積分が簡単に実行できる形にすれば良いと思っています。
このような円の面積などのような場合には次のような方法も有効的です。
(1-B)微小面積(体積)を幾何学的に計算して積分する方法

求めたい面積\(S\)は、変数を\(x,y\)とすると、
として微小面積について\(x\)と\(y\)について足し合わせればよい。
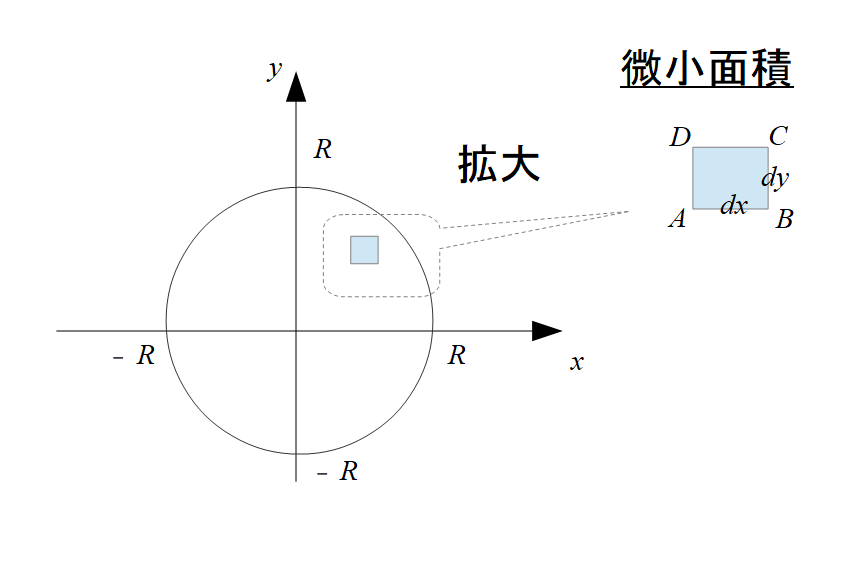

この時の微小面積(ABCD)は、\(dx\,dy\)と書けます(デカルト座標での表記)が、これが唯一の表記方法ではないはずです。
下記のように、変数を\(r\)と\(\theta\)にした極座標表示で書いても良いです。
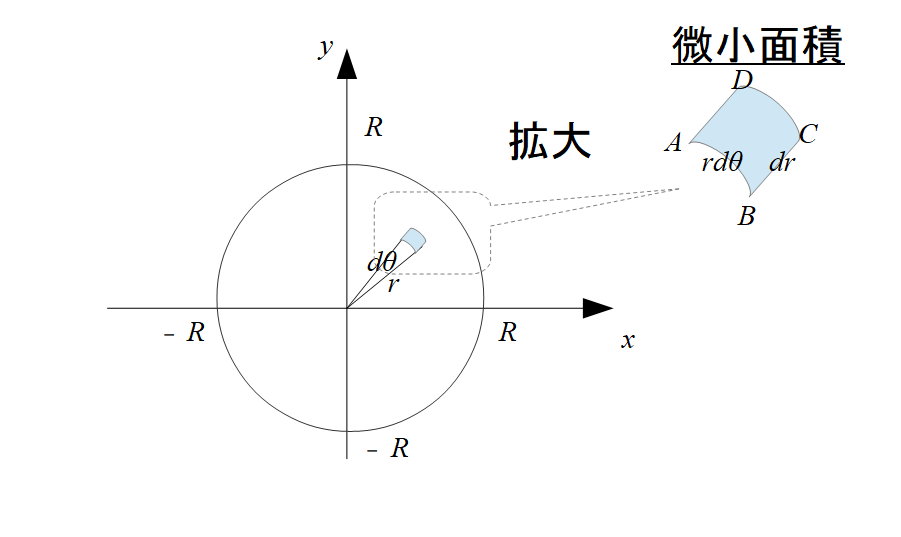

この時の微小面積(ABCD)は、\(r\,d\theta\, dr\)になります。
※念のためですが、微小面積は少し四角形とは形が崩れて見えています。長さでいうと\(AB \neq CD\)です。
しかし、CDは厳密には\((r+dr)\,d\theta\)と書けますが、微小量の2次以上は消去するとすると、結局\(r\,d\theta+dr\,d\theta\simeq r\,d\theta\)となるので、\(AB=CDと\)なります。
このように簡単な場合は微小面積は幾何学的に求めることができるので、求めたい面積\(S\)というのは、
となります。
ここで、変数\(r\)と\(\theta\)の範囲は、
\(0\leq r\leq R\)
\(0\leq \theta \leq 2\pi\)
なので、(9)式の積分すると、
S=\int_{0}^{R}\int_{0}^{2\pi} r\,dr\,d\theta=2\pi\bigg[\frac{r^2}{2}\bigg]_{0}^{R}=\pi R^2\cdot\cdot\cdot (10)\end{align*}
となります。
面積公式と同じ値になりました。
(1-C)ヤコビ行列を使用する方法


(1-B)の方法と似ているのですが、座標変換をして面積を求める方法を紹介します。
円の面積を求めるので、何もデカルト座標で頑張って面積を求める必要はないです。
下記のように極座標表示に変数を変換して、面積を求めても良いです。
むしろ面積が求めやすいように自由に変数を変換して計算した方が計算が楽です。
(1-B)の方法は、微小面積が視覚的にわかりやすいので、微小面積を計算してそこから面積\(S\)を計算しましたが、今から紹介する「変数変換による面積を求める方法」は、より一般的な変数変換の面積計算にも使えます。
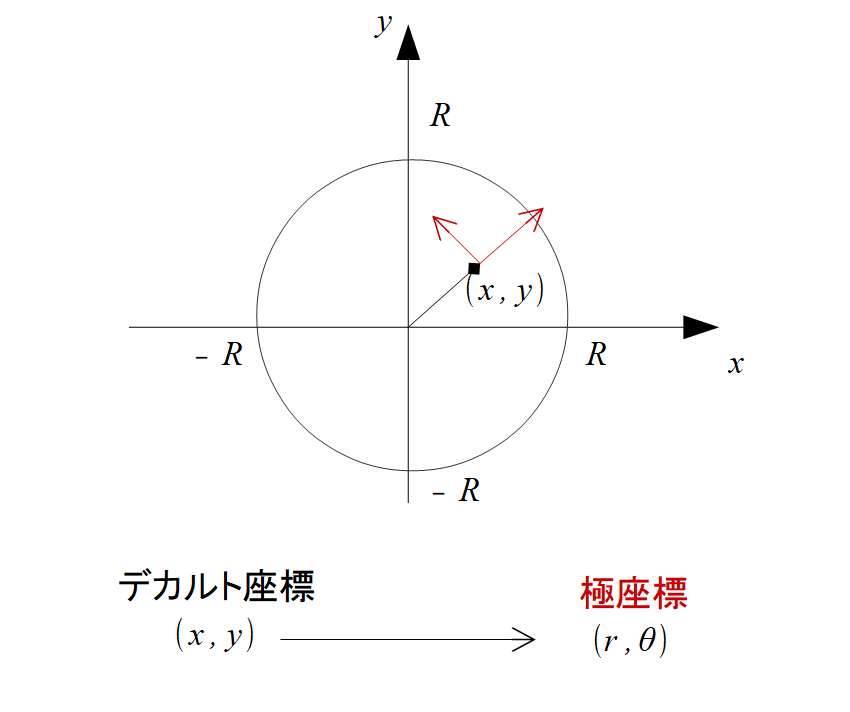

このように座標をデカルト座標\((x,y)\)から極座標\((r,\theta)\)に変換します。
\(x,y\)は\(r,\theta\)を独立な変数として持ちます。
逆に、
\(r,\theta\)は、\(x,y\)を独立な変数として持ちます。
実際、(11)(12)から、
\theta(x,y)=\tan^{-1}\frac{y}{x}\cdot\cdot\cdot (14)\end{align*}
と書けます。
求めたい面積は、
なのですから、\(dx\),\(dy\)が必要なります。
全微分公式より、
これを求めるのに、
\(\frac{\partial x}{\partial r}=\cos\theta\)
\(\frac{\partial x}{\partial \theta}=\sin\theta\)
\(\frac{\partial x}{\partial r}=-r\sin\theta\)
\(\frac{\partial x}{\partial \theta}=r\cos\theta\)
だから、(15)(16)式は、
これを行列式にすると、
よって、(21)式は、
だから求めたい面積\(S\)は、
となります。
(1-B)で示した(9)式と同じ結果になりました。
このようにして変数変換を行って、微小面積は「ヤコビ行列」で変数変換前と後を結びつける((21)式)ことで、求めたい面積が簡単に求まります。
ではこの(1-C)の方法を使って、円の面積ではなく楕円の面積を求めてみましょう。
楕円の面積
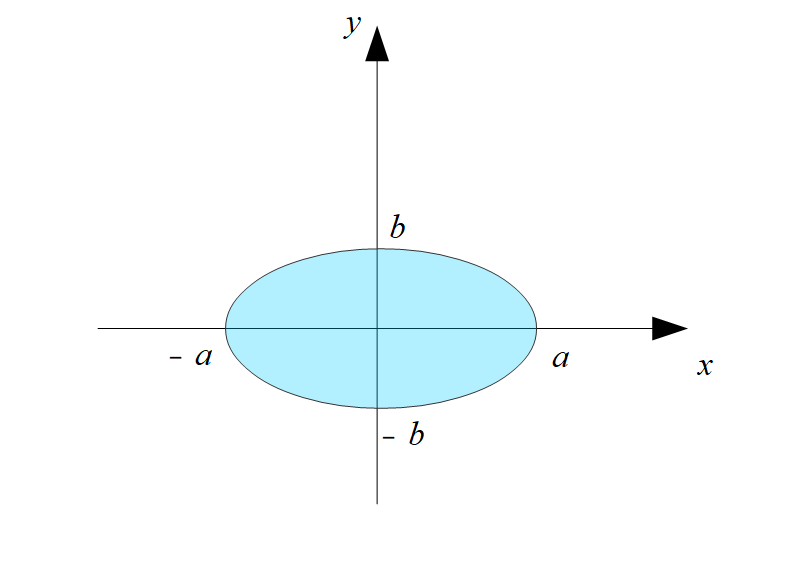

\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)の内部の面積を求めることになります。
つまり、
\(\frac{x^2}{a^2}+\frac{y^2}{b^2} \leq 1\)である領域の面積を求める。
変数\(x,y\)の領域は、
\(-a \leq x \leq a\)
\(-b \leq y \leq b\)
です。
もちろん(1-A)の方法で計算することもできますが、面倒なので(1-C)の方法を駆使して楕円の面積を求めたいと思います。
(2-C)ヤコビ行列を使用する方法

まず、楕円のまま面積を計算するのはめんどうなので、楕円を円に変換してやりましょう。
それは、
\(x=au\)\((-1 \leq u \leq1)\)
\(y=bv\)\((-1 \leq v \leq1)\)
とすれば良いです。
このとき、楕円の面積\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)が、
になります。


では、求めたい面積、
を計算するにあたって、ヤコビ行列を用いて微小面積を変換します。
であり、
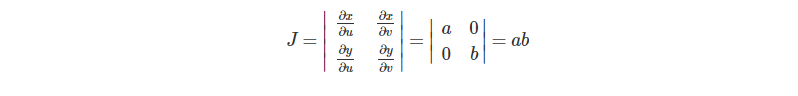
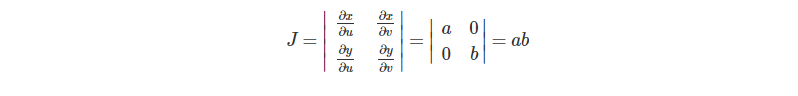
よって、(26)式に代入して、
だから求めたい面積は、
もうここまで来たら、\(du\,dv\)を積分した値は「半径1の円の面積と同じ(\(\pi 1^2\))」だから、
楕円の面積の公式通りの値になりましたね。
結果は、公式通りになったので公式を覚えておけば良いわけですが考え方は非常に重要です。
球の体積
球の体積
\(x^2+y^2+z^2\leq R^2\)
\(-R\leq x\leq R\)
\(-R\leq y\leq R\)
\(-R\leq z\leq R\)
の領域の体積を計算することになります。
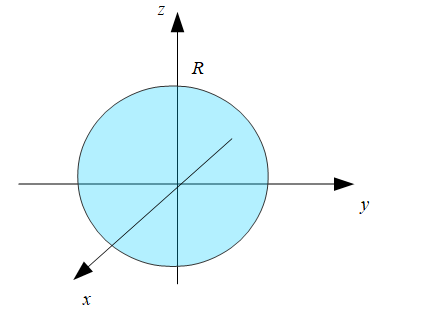

ちなみにこれを\(R\)で微分すると、表面積の\(4\pi R^2\)になります。
それは後ほど明らかになるでしょう。
(3-B)微小面積(体積)を幾何学的に計算して積分する方法
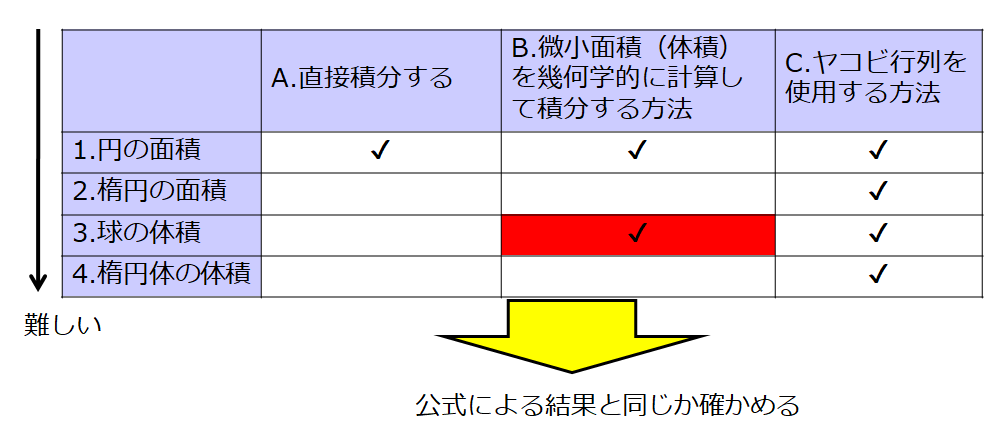

繰り返しになりますが、球の体積であったとしても(A)の方法でももちろん計算は可能です。
しかし、(A)の方法はあくまでデカルト座標での積分の方法であって球を表現するのに必ずしもデカルト座標で考えることが良いとは限らないので積分の方法もそれに適した方法を選択する方が良いでしょう。
まずは、微小体積を幾何学的に計算してみましょう。
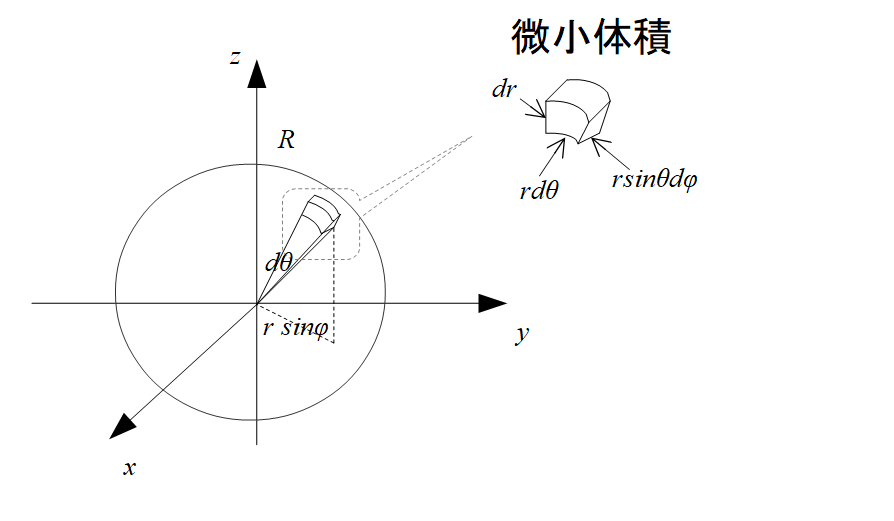

微小体積は絵の通り、
\(dV=r^2\sin\theta\, dr\, d\phi \,d\theta\)
だから求める体積は、
積分区間は、
\(0\leq r\leq R\)
\(0\leq \phi\leq 2\pi\)
\(0\leq \theta\leq \pi\)
だから、
となり、公式通りになります。
ちなみに・・・表面積と体積の関係性について・・・
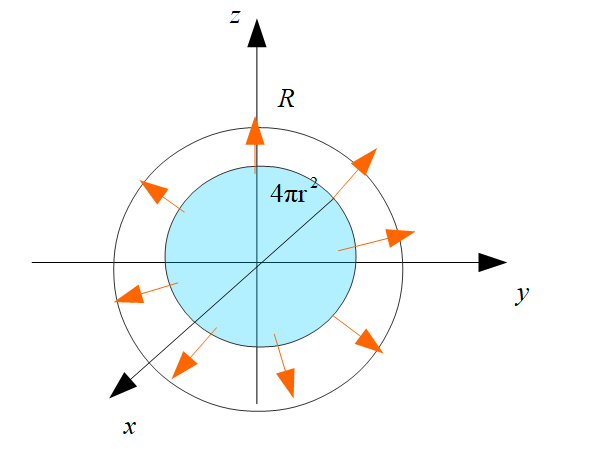
このように表面積を仮に\(4\pi r^2\)と知っていたとします。
球の体積は表面積を\(r\)方向に積算していった値であると考えれば、
となり、球の表面積と体積は微分積分の関係にあることが理解できます。
もちろん(27)式の\(r\)以外の積分を先にやってしまっても同じ結果が出てきます。
(3-C)ヤコビ行列を使用する方法
3変数になるので少々複雑になりますが、基本的な手続きは同じです。
求めたい体積は、
です。
ここで、変数変換をしましょう。
\(x=r\sin\phi\cos\theta\)
\(y=r\sin\phi\sin\theta\)
\(z=rcos\theta\)
それぞれの変数の範囲は、
\(0\leq r\leq R\)
\(0\leq \phi\leq 2\pi\)
\(0\leq \theta\leq \pi\)
では、微小体積はどのようになるかと言いますと、
ここでヤコビ行列式
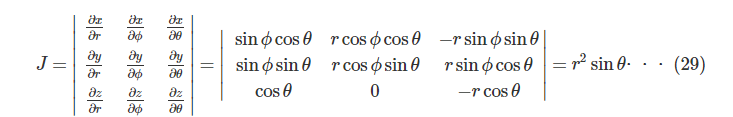
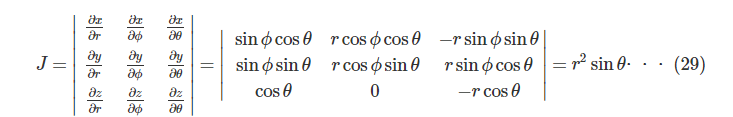
ゆえに、求めたい体積は、
※計算過程は(30)式と同じなので省略
よって公式通りの結果になりました。
では最後に楕円の体積を求めてみましょう。
これは楕円の面積を求めた方法と手順は同じで、もう既に手法は紹介し尽くしているので結構簡単に結果を導くことができます。
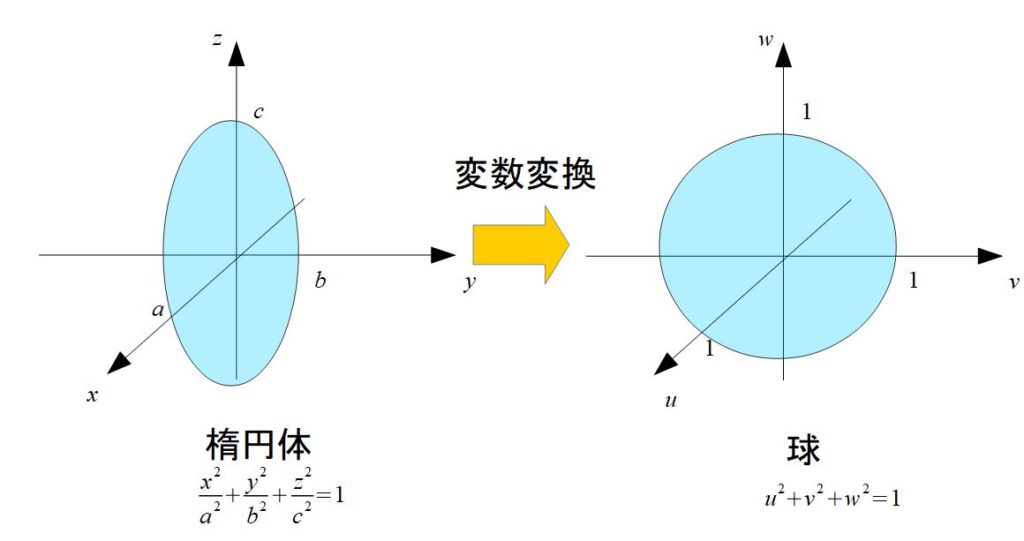
楕円体の体積
楕円体
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\leq 1\)
\(-a\leq x\leq a\)
\(-b\leq y\leq b\)
\(-c\leq z\leq c\)
の領域の体積を計算することになります。


(3-C)ヤコビ行列を使用する方法

まず、楕円体のまま体積を計算するのはめんどうなので、楕円体を球体に変換してやりましょう。
それは、
\(x=au\) \((-1 \leq u \leq1)\)
\(y=bv\) \((-1 \leq v \leq1)\)
\(z=cw\) \((-1 \leq w \leq1)\)
とすれば良いです。
このとき、楕円体の体積\(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\)が、
になります。

では、求めたい体積、
を計算するにあたって、
ヤコビ行列を用いて微小体積を変換します。
であり、
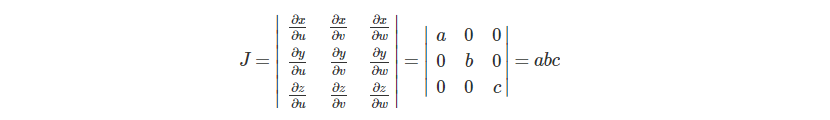
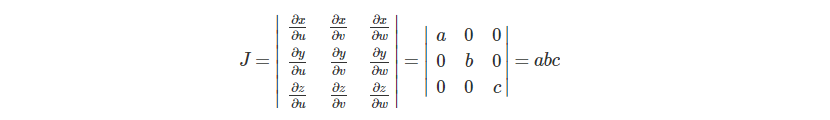
よって、(33)式に代入して、
だから求めたい体積は、
もうここまで来たら、\(du\,dv\,dw\)を積分した値は「半径1の球の体積と同じ(\(\frac{4}{3}\pi 1^3\))」だから、
と、公式通りになりました。
まとめ
今回の内容は以上となります。



色々計算方法を示しましたが、どれも重要なのでよく練習しておく方が良いでしょう(^^)/
おすすめの参考書
最後におすすめの参考書を紹介しておきましょう。
マセマの参考書は大学初学年や、なんだったら高校生でも読めるくらいわかりやすく書かれていますので、「大学数学はキツイな」って感じた方は手に取ってみてください。