どうも(^^)/
前回、等温過程と断熱過程の特徴の違いについて記事にしてみました。
いきなりですが、問題です。
理想気体と仮定し、断熱容器\(V\)の中に\(n\)molの気体を入れておきます。
次の2通りの操作を考えます。
※タイトルは「ピストンを引く」と書いていますが、絵は板っぽいので「板を引く」と表現しておきます。

絵に書くと、↑こんな感じです。
どちらも、容器の初期体積は\(V_{1}\)で、一回目の操作で体積は\(V_{2}\)にします。
最終の容器の体積は、初期状態の容器の体積\(V_{1}\)に戻すことにします。
結論(答え)を急ぎましょう(‘ω’)
1番目の操作「ゆっくり板を引き(操作A)、その後ゆっくり板を押していく(操作B)」においては、最終状態の温度というのは、どうなるかというと・・・・・・初期状態の温度と同じです。
しかし、2番の操作ではどうなるでしょうか?
・・・・・・
何と温度があがります(‘ω’)
ということで理論を解説していきたいと思います。
等温過程と断熱過程での\(p-V\)グラフの違い
その前に、等温過程と断熱過程での\(p-V\)グラフの違いを押さえておきましょう。
理想気体を仮定してます。
理想気体の状態方程式
pV=nRT\tag{1}
\end{align*}
理想気体の状態方程式において、等温準静的過程と断熱準静的過程において以下の関係式が成り立つのですよね。
等温準静的過程の場合
pV=const\tag{2}
\end{align*}
断熱準静的過程の場合
pV^{\gamma}=const\tag{3}
\end{align*}
※\(\gamma\):比熱比(\(1\leq\gamma \leq \frac{5}{3}\))
これを\(p-V\)グラフで描くと、下記のようになります。
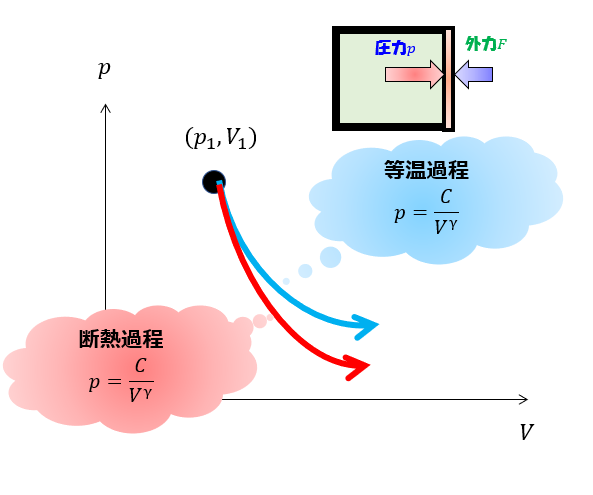

断熱準静的過程の方が、何やら急な勾配を持っていますね。
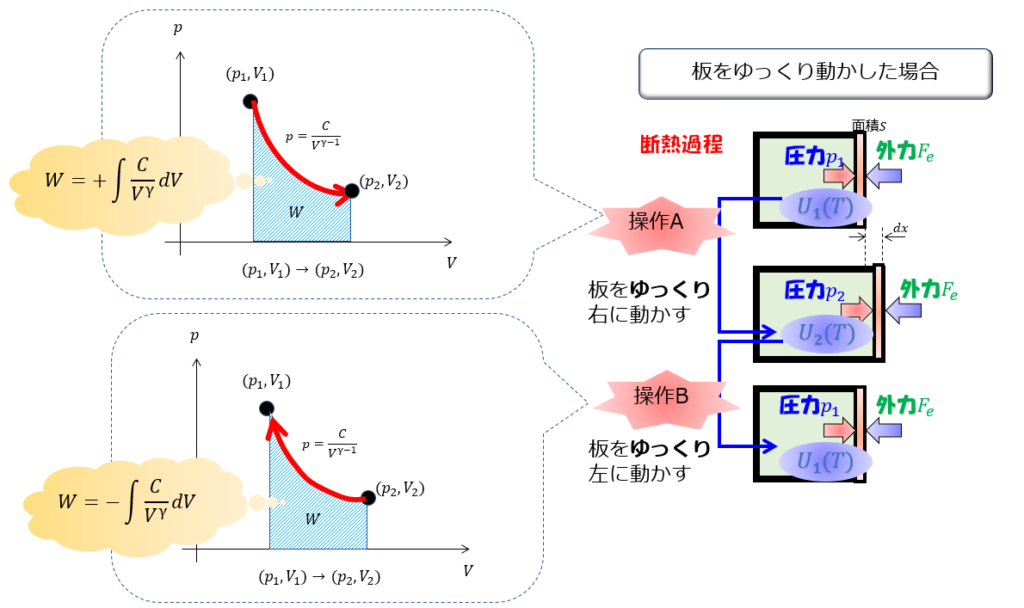
ゆっくり板を引き(操作A)、その後ゆっくり板を押していく(操作B)
1番の操作は、引く場合(気体が膨張する)も押す場合(気体が圧縮する)もゆっくり行っているので、準静的過程です。
しかも、断熱容器なので熱の出入りもありません。
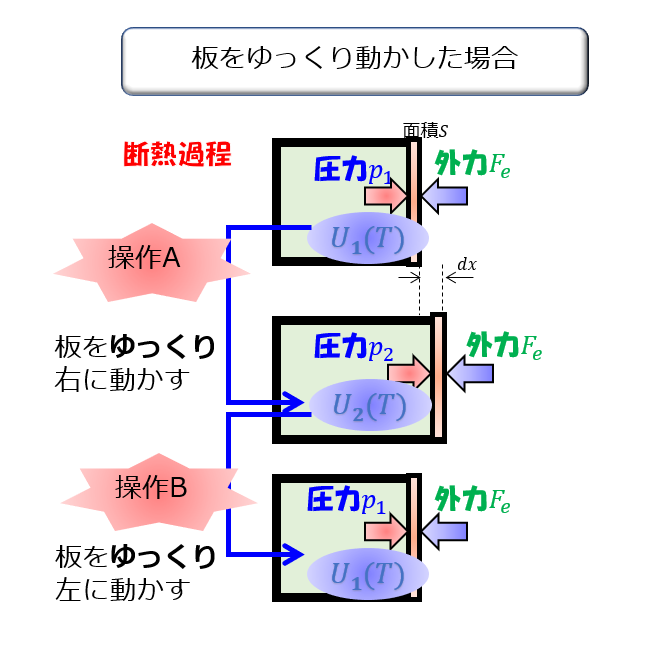

この場合は、下記の\(p-V\)グラフでもわかるように、行って帰ってきただけなので、気体の正味の仕事量は何もしていないことになります。

熱力学の第一法則
Q=\Delta U+ W\tag{4}
\end{align*}
断熱容器なので、\(Q=0\)であるため、
0=\Delta U+ W\tag{5}
\end{align*}
です。
要するに、気体が仕事をしていないということであれば、内部エネルギーは全然変わっていないということになります。
ところで、内部エネルギーが変わっていないということはどういう意味を持つのでしょうか?
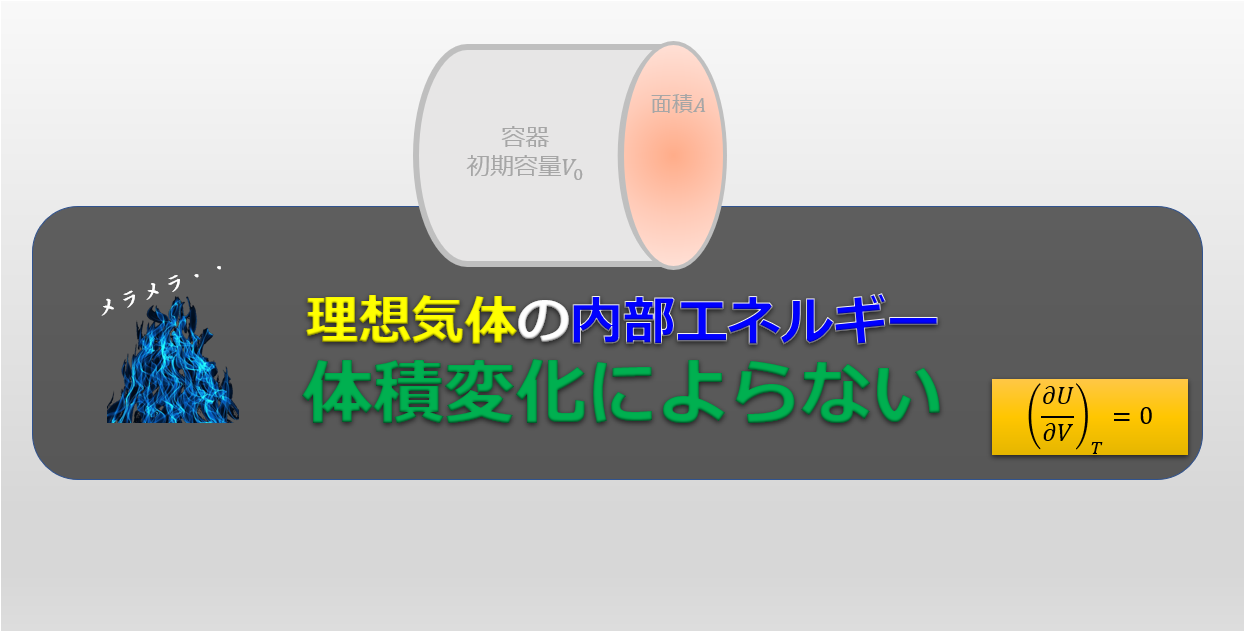
理想気体の場合は、内部エネルギーは温度にしか依存しなかったのです。
内部エネルギー:\(U(T)\)
です。
ということは、温度が変わっていないということです。
そりゃ、気体が膨張に使った仕事量を、外から押してあげてもう一度元の状態に戻したのですから、「はい、元通り(^^)/」って感じでしょう。
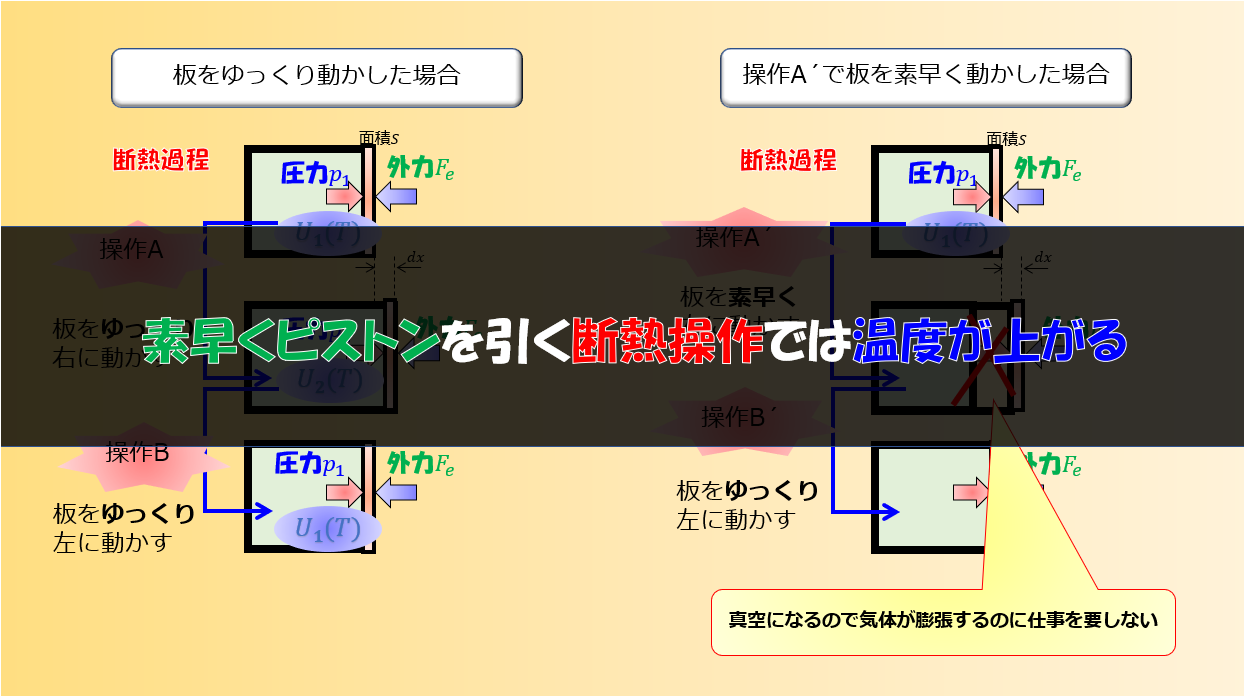
素早く板を引き(操作A´)、その後ゆっくり板を押していく(操作B´)
2番目の操作は少々ややこしいので、操作A´と操作B´を順に説明していくことにします(^^)/
操作A´
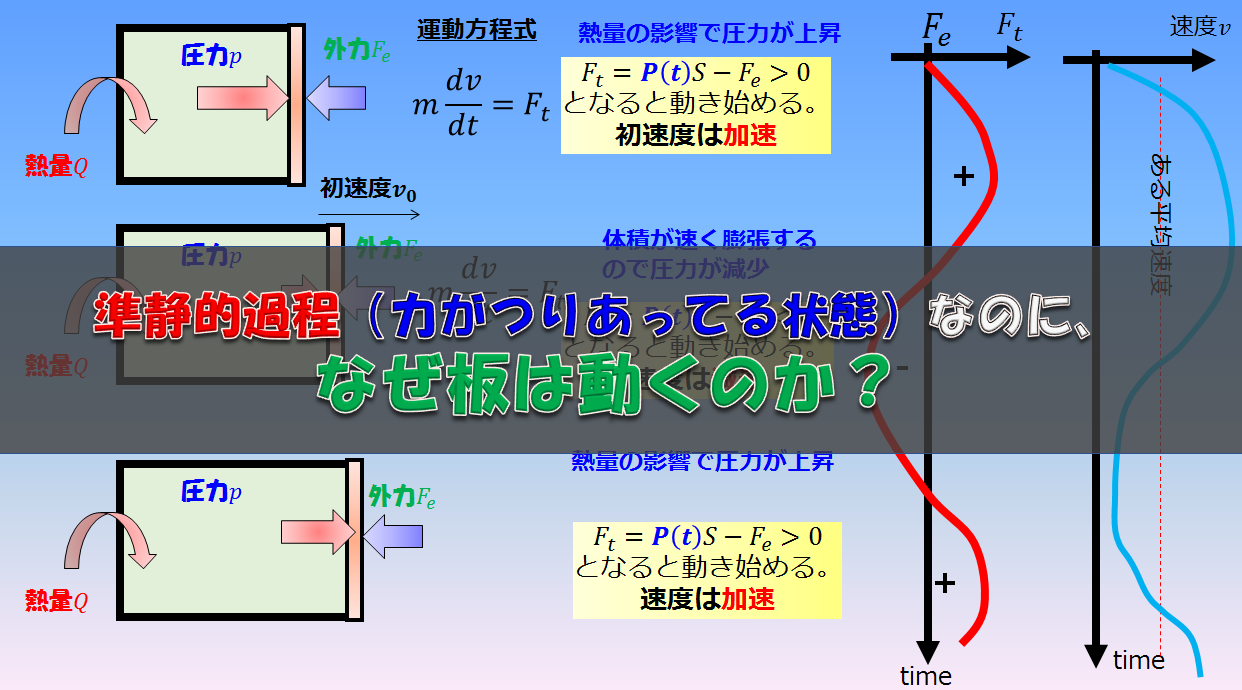
操作A´では、素早く引く過程では準静的過程ではありません。
このような操作では、とても熱平衡状態を保っているとは言えず、いわゆる非平衡な状態が作られています。


この操作はただの断熱過程です。
気体が膨張するにあたって、何も邪魔するものがいない(真空)ので、気体が膨張するのに仕事を要しないということに注意しましょう。
ちなみに、非平衡状態では熱力学でのマクロな物理量である圧力や温度などが定義できないので、これでは恩恵を受けることができません。
操作A´のあとに熱平衡状態になるまでしばらく待つことにします。
そしてようやく熱平衡状態になったところで、ゆっくりと板を押すことを考えます(操作B´)。
この操作B´過程は準静的過程です。
操作A´のときの「素早く引く」というのは、気体の膨張スピードがついてこれないくらいであるものとします。
どれくらい素早くかというと、音速くらいのスピードで板を右に動かしたと思ってください。
断熱準静的過程であるので、これは\(p-V\)グラフを書くとわかりやすいです。
しかし、ここで注意が・・・・
素早く板を引く場合の操作(操作A´)は、準静的過程ではないので\(p-V\)に書くことができません。
※点線でいちおう書きますが、操作A´では、気体は仕事量を必要とせずに体積\(V_{2}\)まで状態がジャンプしたということになります。
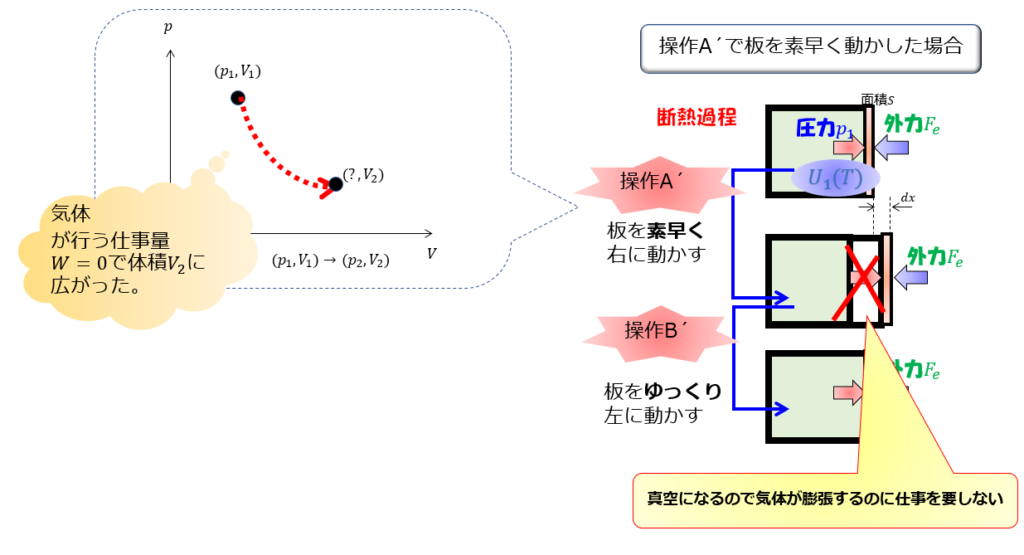

では、操作A´のときの内部エネルギーはどうなっているのでしょうか。
またまた熱力学の第一法則を持ってきます。
0=\Delta U + W\tag{5}
\end{align*}
素早く板を引くと、気体がついてこれないために、気体と板に真空ができます。
そうすると、気体にとって何の障壁もない状態になりますよね(外圧がない状態)。
ならば、系(気体)は全く抵抗を受けずに膨張することができます。
つまり、系(気体)が外部にする仕事量は0です。
そうすると、(5)式を見ると、
\Delta U=0\tag{6}
\end{align*}
です。
内部エネルギーが変わっていません。
ということは、理想気体での内部エネルギーは温度のみの関数なので、温度も変わっていません。
この素早く板を引く場合の操作(操作A´)は、準静的過程ではないですが、あえて\(p-V\)グラフに無理やり書くと・・・・
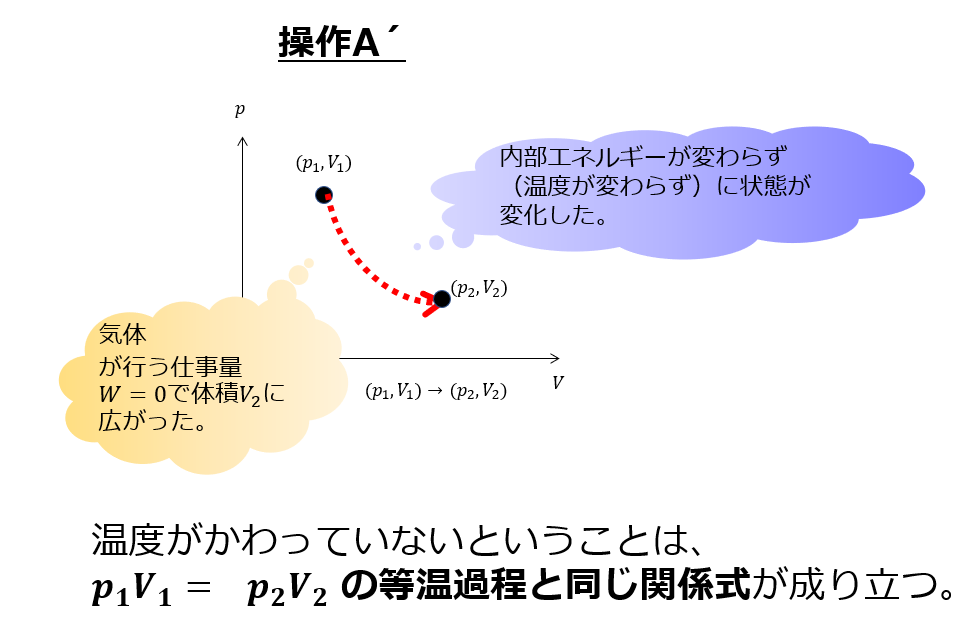

はい、こんな感じです。
繰り返しになりますが操作A´では知らない間に、系(気体)の状態はジャンプしたことになります。
しかも、温度が変わっていないので、初期の状態と最終の状態は、
p_{1}V_{1}=p_{2}V_{2}\tag{6}
\end{align*}
が成り立ちます。
本当は、操作A´では熱平衡状態ではないので、操作の最中で熱力学のマクロ物理量が定義できないため、\(p-V\)グラフ上には軌跡を表現できないのですが、上の絵ではわかりやすくするため等温過程のような奇跡を点線で表現しています。
操作B´
その状態でです・・・・・ゆっくりと押すという操作B´を行います。
この操作のときは、準静的過程であり常に平衡状態であるために、\(p-V\)グラフで表現することができます。
わかりやすくするために、「等温準静的過程\(pV=const\):点線」と「断熱準静的過程\(pV^{\gamma}\):実線」を載せておきます。
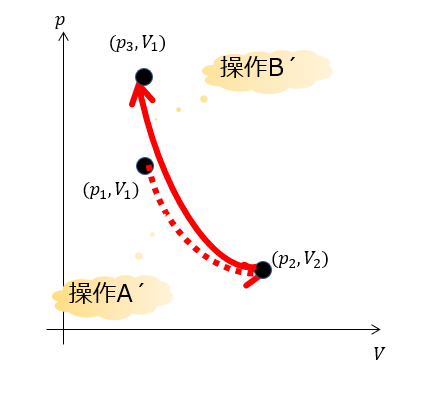

冒頭で「等温準静的過程」と「断熱準静的過程」の\(p-V\)グラフの勾配の違いを示しましたように、断熱準静的過程ではグイっと勾配が大きいので、元の容器の体積に戻したとしても圧力が大きくなっていますよね。
つまり、\(pV=nRT\)から温度が上昇しているという結論になります。
ポアッソンの関係式を上手く使って証明することもできますね。
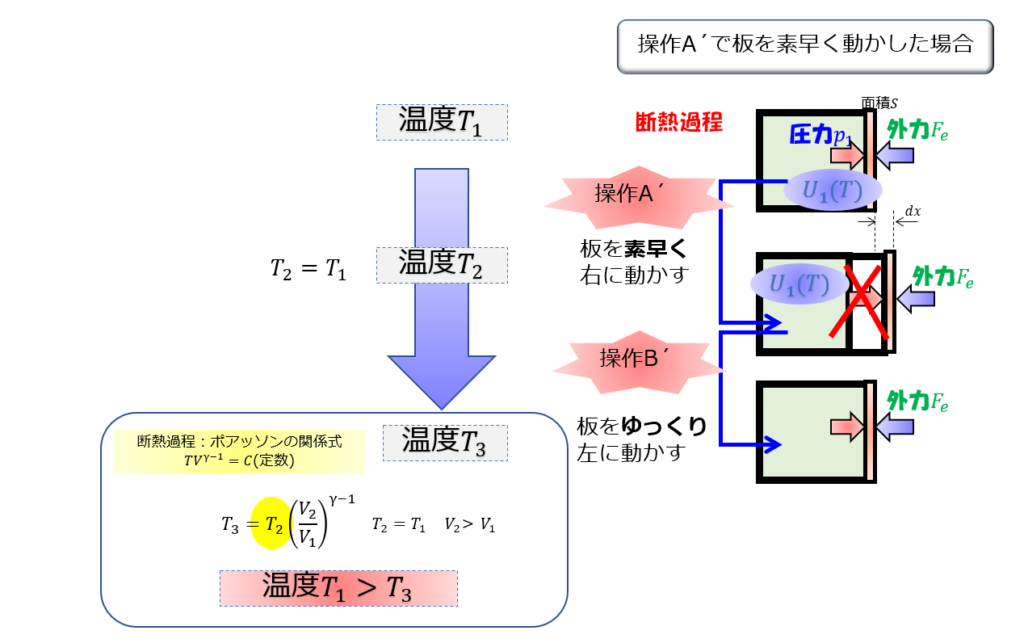

なぜ2番の操作で温度が上昇するのか?
2番の温度が上昇したのは、やはり操作A´で容器が膨張したのに・・・・知らない間に系(気体)が膨張したという点でしょうかね。
気体が膨張するのには、外部からの力を受けるために、幾分か労力がいるわけです。
それなのに、真空なので簡単に膨張できてしまったのです。
つまり、系(気体)は何も状態は変わっていないのに、容量だけが大きくなることに成功したということです。
これが内部エネルギーが変わっていないということの言い換えですかね(^^)
その状態で、外部からじっくり仕事をしてもらったので、系(気体)はめちゃくちゃ元気になった・・・と、こんな感じで考えても良いでしょうかね。
ゆえに、温度上昇につながったということです。
まとめ
理想気体と仮定し、断熱容器\(V\)の中に\(n\)molの気体を入れておきます。
次の2つの操作を考えます。
最終状態の温度はどうなっているのか?
- ゆっくり板を引き(操作A)、その後ゆっくり板を押していく(操作B)
→最終状態の温度は、最初の温度と同じ。 - 素早く板を引き(操作A´)、その後ゆっくり板を押していく(操作B´)
→最終状態の温度は、最初の温度より上がる。



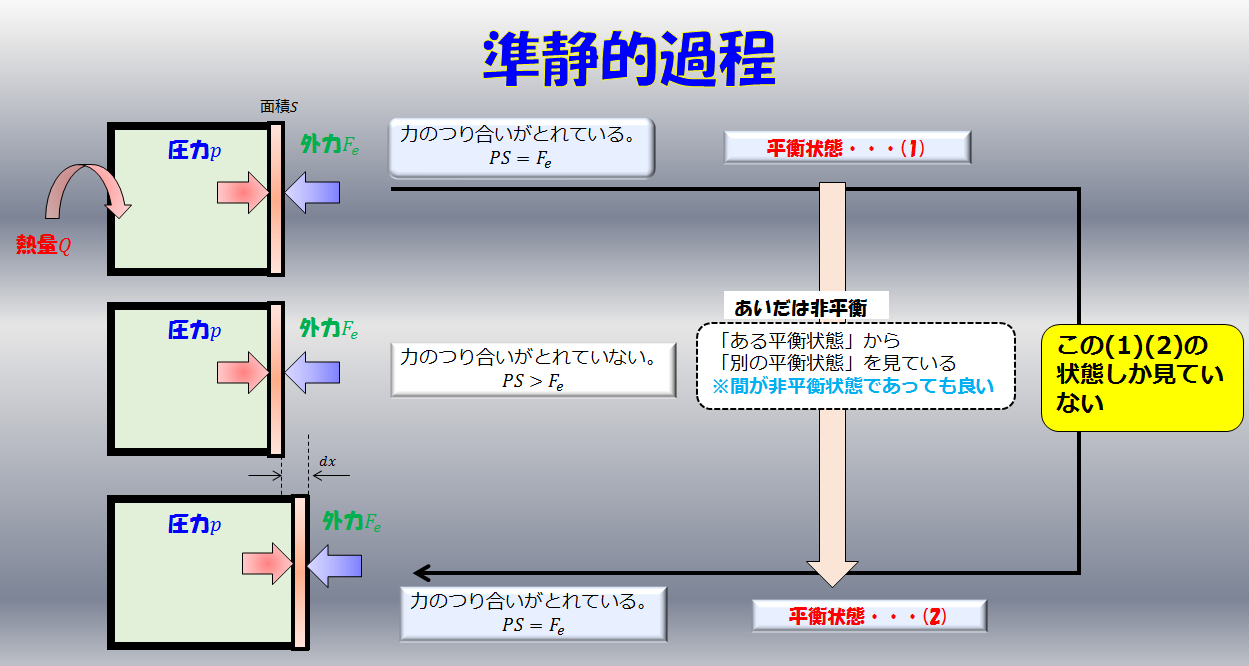
熱力学はある熱平衡状態から別の熱平衡状態の変化しか見ていない
熱力学では、ある熱平衡状態から別の平衡状態への変化しか見ていないので、このような詳細な議論というのはできません。
つまり始点と終点しか見ていないのですよね。
操作A´の最中はどうなっているのでしょうか。
この考察については、追々考えて追加していきたいと思います。
↓今考えていること
始点と終点のその間の動きを考えるのであれば、操作A´では気体が膨張するのに気体の運動エネルギーが内部エネルギーを変化させない、つまり維持する方向にうまく働いたと考えられるのではないでしょうかね・・・・・。
普通、気体が膨張すると、圧力が下がるなどの内部状態のエネルギーは下がりそうですよね。
しかし、今回の場合は内部エネルギーが変わっていません。
これは系(気体)が膨張すると、内部エネルギーが下がる方向なのですが、運動エネルギーの分で内部エネルギーを変えないように補ってくれていると考えても良いかと思います。