こんにちは(@t_kun_kamakiri)。
前回の記事では、「2次元の拡散方程式」をGoogle Colabでアニメーション作成を行いました。
前回の記事はこちら
今回は、以下のような２次元のバーガース方程式をPythonで実装します。
今日作成する動画は以下のような感じになる・・・予定でしたがあまりうまくいきませんでした_(._.)_
前回の記事と同じ方法で動画を作成したのですが( ﾉД`)
１次元のバーガース方程式については、以前の記事でも書きましたが今回はその２次元バージョンというわけです。
カマキリ
今日もゆる～く学びます(^^)/
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
こんな人が対象
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
本記事シリーズの最終目標は、ナビエストークス方程式をPythonで実装することですが、いきなりナビエストークス方程式を実装するのは難しいので各項の意味を確認しながら進めていきたいと思います。
今回の内容はこちら
- ２次元のバーガース方程式をPythonで数値計算
- ２次元のアニメーションをGoogle Colabで作成（※あまりうまくいかなかった）
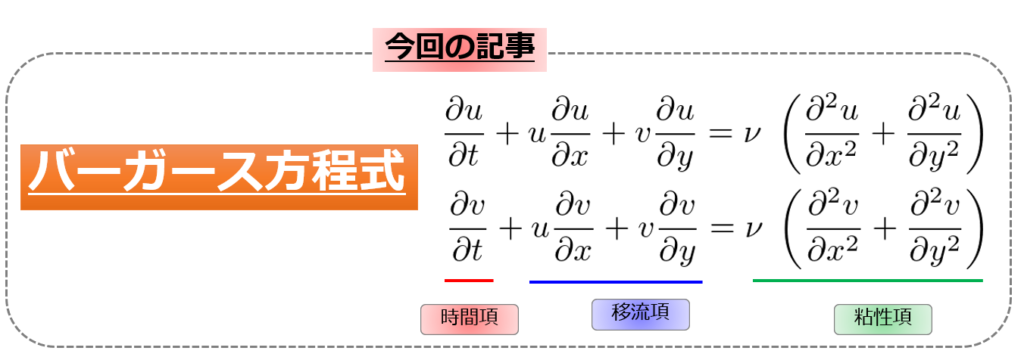
2次元のバーガース方程式
まずは、解くべき方程式の確認を行いましょう。
\begin{align*}
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = \nu \; \left(\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2}\right)\\
\frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} = \nu \; \left(\frac{\partial ^2 v}{\partial x^2} + \frac{\partial ^2 v}{\partial y^2}\right)\tag{1}
\end{align*}
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = \nu \; \left(\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2}\right)\\
\frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} = \nu \; \left(\frac{\partial ^2 v}{\partial x^2} + \frac{\partial ^2 v}{\partial y^2}\right)\tag{1}
\end{align*}
これを数値計算できるように空間微分に対して2次精度の中心差分を施して以下のように離散化します。
\begin{align*}
\begin{split}
& \frac{u_{i,j}^{n+1} – u_{i,j}^n}{\Delta t} + u_{i,j}^n \frac{u_{i,j}^n-u_{i-1,j}^n}{\Delta x} + v_{i,j}^n \frac{u_{i,j}^n – u_{i,j-1}^n}{\Delta y} = \\
& \qquad \nu \left( \frac{u_{i+1,j}^n – 2u_{i,j}^n+u_{i-1,j}^n}{\Delta x^2} + \frac{u_{i,j+1}^n – 2u_{i,j}^n + u_{i,j-1}^n}{\Delta y^2} \right)
\end{split}\\
\begin{split}
& \frac{v_{i,j}^{n+1} – v_{i,j}^n}{\Delta t} + u_{i,j}^n \frac{v_{i,j}^n-v_{i-1,j}^n}{\Delta x} + v_{i,j}^n \frac{v_{i,j}^n – v_{i,j-1}^n}{\Delta y} = \\
& \qquad \nu \left( \frac{v_{i+1,j}^n – 2v_{i,j}^n+v_{i-1,j}^n}{\Delta x^2} + \frac{v_{i,j+1}^n – 2v_{i,j}^n + v_{i,j-1}^n}{\Delta y^2} \right)
\end{split}\tag{2}
\end{align*}
\begin{split}
& \frac{u_{i,j}^{n+1} – u_{i,j}^n}{\Delta t} + u_{i,j}^n \frac{u_{i,j}^n-u_{i-1,j}^n}{\Delta x} + v_{i,j}^n \frac{u_{i,j}^n – u_{i,j-1}^n}{\Delta y} = \\
& \qquad \nu \left( \frac{u_{i+1,j}^n – 2u_{i,j}^n+u_{i-1,j}^n}{\Delta x^2} + \frac{u_{i,j+1}^n – 2u_{i,j}^n + u_{i,j-1}^n}{\Delta y^2} \right)
\end{split}\\
\begin{split}
& \frac{v_{i,j}^{n+1} – v_{i,j}^n}{\Delta t} + u_{i,j}^n \frac{v_{i,j}^n-v_{i-1,j}^n}{\Delta x} + v_{i,j}^n \frac{v_{i,j}^n – v_{i,j-1}^n}{\Delta y} = \\
& \qquad \nu \left( \frac{v_{i+1,j}^n – 2v_{i,j}^n+v_{i-1,j}^n}{\Delta x^2} + \frac{v_{i,j+1}^n – 2v_{i,j}^n + v_{i,j-1}^n}{\Delta y^2} \right)
\end{split}\tag{2}
\end{align*}
空間微分に対しては、数値計算の安定性のために後退差分で行います。
今、ほしい情報はn+1ステップでの\(u^{n+1}\)や\(v^{n+1}\)の値ですので、式変形して、
\begin{align*}
u_{i,j}^{n+1} = & u_{i,j}^n – \frac{\Delta t}{\Delta x} u_{i,j}^n (u_{i,j}^n – u_{i-1,j}^n) – \frac{\Delta t}{\Delta y} v_{i,j}^n (u_{i,j}^n – u_{i,j-1}^n) \\
&+ \frac{\nu \Delta t}{\Delta x^2}(u_{i+1,j}^n-2u_{i,j}^n+u_{i-1,j}^n) + \frac{\nu \Delta t}{\Delta y^2} (u_{i,j+1}^n – 2u_{i,j}^n + u_{i,j-1}^n)\\
v_{i,j}^{n+1} = & v_{i,j}^n – \frac{\Delta t}{\Delta x} u_{i,j}^n (v_{i,j}^n – v_{i-1,j}^n) – \frac{\Delta t}{\Delta y} v_{i,j}^n (v_{i,j}^n – v_{i,j-1}^n) \\
&+ \frac{\nu \Delta t}{\Delta x^2}(v_{i+1,j}^n-2v_{i,j}^n+v_{i-1,j}^n) + \frac{\nu \Delta t}{\Delta y^2} (v_{i,j+1}^n – 2v_{i,j}^n + v_{i,j-1}^n)\tag{3}
\end{align*}
u_{i,j}^{n+1} = & u_{i,j}^n – \frac{\Delta t}{\Delta x} u_{i,j}^n (u_{i,j}^n – u_{i-1,j}^n) – \frac{\Delta t}{\Delta y} v_{i,j}^n (u_{i,j}^n – u_{i,j-1}^n) \\
&+ \frac{\nu \Delta t}{\Delta x^2}(u_{i+1,j}^n-2u_{i,j}^n+u_{i-1,j}^n) + \frac{\nu \Delta t}{\Delta y^2} (u_{i,j+1}^n – 2u_{i,j}^n + u_{i,j-1}^n)\\
v_{i,j}^{n+1} = & v_{i,j}^n – \frac{\Delta t}{\Delta x} u_{i,j}^n (v_{i,j}^n – v_{i-1,j}^n) – \frac{\Delta t}{\Delta y} v_{i,j}^n (v_{i,j}^n – v_{i,j-1}^n) \\
&+ \frac{\nu \Delta t}{\Delta x^2}(v_{i+1,j}^n-2v_{i,j}^n+v_{i-1,j}^n) + \frac{\nu \Delta t}{\Delta y^2} (v_{i,j+1}^n – 2v_{i,j}^n + v_{i,j-1}^n)\tag{3}
\end{align*}
上記のような偏微分方程式の場合は、時々刻々と変化する物理量（今の場合は流速）に対して解くので初期状態を設定しないと解くための種がありません。
というわけで、初期状態を設定します。
というわけで、初期状態を設定します。
初期状態の設定
初期状態を以下のようにします。
\begin{align*}
u,\ v\ = \begin{cases}\begin{matrix}
2 & \text{for } x,y \in (0.5, 1)\times(0.5,1) \cr
1 & \text{それ以外}
\end{matrix}\end{cases}\tag{4}
\end{align*}
u,\ v\ = \begin{cases}\begin{matrix}
2 & \text{for } x,y \in (0.5, 1)\times(0.5,1) \cr
1 & \text{それ以外}
\end{matrix}\end{cases}\tag{4}
\end{align*}
さらに、数値計算は有限の大きさに対して解くので計算領域の端に対して数値を設けないと問題を解くことができません。
なので、以下のように境界条件を設定します。
境界条件の設定
境界条件を以下のようにします。
\begin{align*}
u = 1,\ v = 1 \text{ for } \begin{cases} \begin{matrix}x=0,2\cr y=0,2 \end{matrix}\end{cases}
\end{align*}
u = 1,\ v = 1 \text{ for } \begin{cases} \begin{matrix}x=0,2\cr y=0,2 \end{matrix}\end{cases}
\end{align*}
では、Pythonを使って2次元の移流方程式を解いてみましょう。
Pythonの使用環境はGoogle Colabとします。
2次元のバーガース方程式をPythonで実装する
まずは必要なライブラリをインポートします。
|
1 2 3 4 |
import numpy as np from matplotlib import pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D |
次に、「条件設定」と「初期状態設定」を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
#条件設定 nx = 41 ny = 41 nt = 120 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) sigma = .0009 nu = 0.01 dt = sigma * dx * dy / nu x = np.linspace(0, 2, nx) y = np.linspace(0, 2, ny) #初期状態の設定 u = np.ones((ny, nx)) v = np.ones((ny, nx)) un = np.ones((ny, nx)) vn = np.ones((ny, nx)) comb = np.ones((ny, nx)) u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 v[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 |
では、初期状態のプロファイルを確認してみましょう！
Matplotlibを使って可視化してみます。
|
1 2 3 4 5 6 7 |
fig = plt.figure(figsize=(8, 5), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) ax.plot_surface(X, Y, u[:], cmap=cm.viridis, rstride=1, cstride=1) ax.plot_surface(X, Y, v[:], cmap=cm.viridis, rstride=1, cstride=1) ax.set_xlabel('$x$') ax.set_ylabel('$y$') |
【結果】
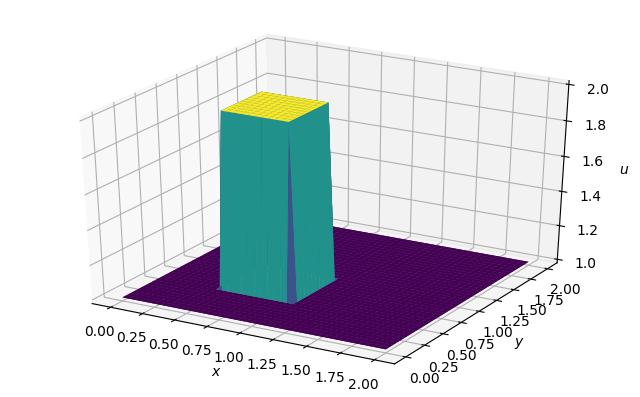
初期状態はこのようになっています。
では、実際にスライスを使って(3)式のバーガース方程式を解いてみましょうの偏微分方程式の離散化を数値計算で求めましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
for n in range(nt + 1): ##loop across number of time steps un = u.copy() vn = v.copy() u[1:-1, 1:-1] = (un[1:-1, 1:-1] - dt / dx * un[1:-1, 1:-1] * (un[1:-1, 1:-1] - un[1:-1, 0:-2]) - dt / dy * vn[1:-1, 1:-1] * (un[1:-1, 1:-1] - un[0:-2, 1:-1]) + nu * dt / dx**2 * (un[1:-1,2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) + nu * dt / dy**2 * (un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1])) v[1:-1, 1:-1] = (vn[1:-1, 1:-1] - dt / dx * un[1:-1, 1:-1] * (vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) - dt / dy * vn[1:-1, 1:-1] * (vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) + nu * dt / dx**2 * (vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2]) + nu * dt / dy**2 * (vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1])) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 v[0, :] = 1 v[-1, :] = 1 v[:, 0] = 1 v[:, -1] = 1 |
こちらの記事で扱ったようにスライスを使っています。
では、最終状態のuのプロファイルを可視化してみてみましょう。
|
1 2 3 4 5 6 7 |
fig = pyplot.figure(figsize=(8, 5), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) ax.plot_surface(X, Y, u, cmap=cm.viridis, rstride=1, cstride=1) ax.set_xlabel('$x$') ax.set_ylabel('$y$') |
【結果】
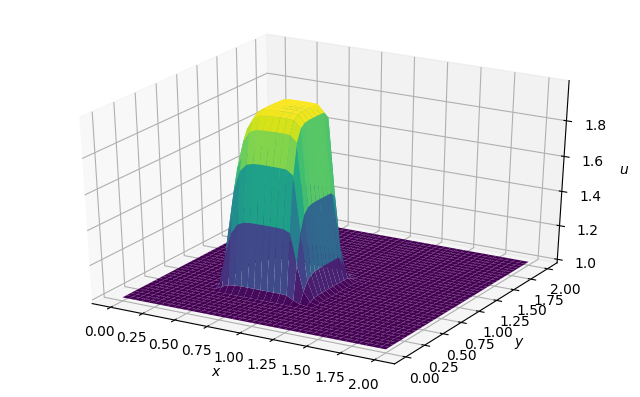
バーガース方程式の特徴は、初期に速度が速い部分はより移動するという特徴があります。
やっぱり静止画よりもアニメーションにして可視化した方が現象の描写として楽しいですよね(^^)/
ってことで、次にGoogle Colabでアニメーション作成する方法について解説します。
カマキリ
あまりうまくいきませんでしたが(笑)
どうせならアニメーションにしたい
先ほどのように静止画でuのプロファイルを見るよりも、やっぱりアニメーションにしたいですよね。
アニメーションの作成には以下の２つあります。
- matplotlib.animation.ArtistAnimation：グラフのオブジェクトのリストを格納することでアニメーションを作成する。
- matplotlib.animation.FuncAnimation：グラフ行進用の関数を用意して逐一更新しながらアニメーションを作成する。
今回は、「matplotlib.animation.FuncAnimation」と使ってアニメーションを作成しています。
カマキリ
以下がPythonのコードです！
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
%%time import numpy as np from matplotlib import pyplot as pyplot from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D #条件設定 nx = 41 ny = 41 nt = 120 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) sigma = .0009 nu = 0.01 dt = sigma * dx * dy / nu x = np.linspace(0, 2, nx) y = np.linspace(0, 2, ny) #初期状態の設定 u = np.ones((ny, nx)) v = np.ones((ny, nx)) un = np.ones((ny, nx)) vn = np.ones((ny, nx)) comb = np.ones((ny, nx)) u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 v[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2 fig = plt.figure(figsize=(8, 5), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) ax.set_xlabel('$x$') ax.set_ylabel('$y$') ax.plot_surface(X, Y, u, rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False) def diffuse(nt): un = u.copy() vn = v.copy() u[1:-1, 1:-1] = (un[1:-1, 1:-1] - dt / dx * un[1:-1, 1:-1] * (un[1:-1, 1:-1] - un[1:-1, 0:-2]) - dt / dy * vn[1:-1, 1:-1] * (un[1:-1, 1:-1] - un[0:-2, 1:-1]) + nu * dt / dx**2 * (un[1:-1,2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) + nu * dt / dy**2 * (un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1])) v[1:-1, 1:-1] = (vn[1:-1, 1:-1] - dt / dx * un[1:-1, 1:-1] * (vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) - dt / dy * vn[1:-1, 1:-1] * (vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) + nu * dt / dx**2 * (vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2]) + nu * dt / dy**2 * (vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1])) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 v[0, :] = 1 v[-1, :] = 1 v[:, 0] = 1 v[:, -1] = 1 ax.set_title('time = '+ str(round(nt*dt,3))+ 'sec, '+ str(nt)+'step') ax.plot_surface(X, Y, u[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=True) |
※計算時間も計測してみました。
【結果】
|
1 2 |
CPU times: user 86.4 ms, sys: 50.1 ms, total: 136 ms Wall time: 76.9 ms |
「76.9ms」が実行にかかった時間ですね。つまり、すぐ終わったってことです。
では、結果のアニメーションを作成してみましょう。
|
1 2 3 |
from IPython.display import HTML ani = animation.FuncAnimation(fig, diffuse, interval = 100,frames = 50) HTML(ani.to_html5_video()) |
※めちゃくちゃ時間がかかりました。
10分くらいは待っていたと思います。
【結果】
おや？
あまりうまくいきませんでした、データがおもすぎるのでしょうか？
カマキリ
何がいけないのか現在調査中_(._.)_
まとめ
今回は、2次元のバーガース方程式をPythonで実装してアニメーション作成を行いました。
前回の記事の内容とあまり変わらず復習程度のないようになりましたが、本記事のシリーズを読むことでPythonを使ったナビエストークス方程式の実装まではいけると思いますので、是非最後までお付き合いくださいm(__)m
次回の記事はこちら
おすすめの書籍紹介
ネット上には無料で多くのことが学べるのですが、ネット情報だけだと情報が偏ったりします。
やっぱり書籍を手に取って体系だって学んだ方が良い場合も多いです。
初心者でもので体系だって学ぶことができる、且つあまり難しすぎない書籍をここで紹介しておきます。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
（本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません）
僕自身もこの書籍ではじめは勉強しました。
小難しい余計なことが書いていないし、年末の一週間くらいで読むことができたので、初心者の方にはとてもお勧めです。
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと！！って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学１年生で偏微分を学んだ方にとってはちょうどよい参考書です。
数値流体の書籍
本記事で紹介している数値計算手法は、多くの数値解法のごく一部です。
特に、非線形方程式で記述できる流体現象のようなものは注意深く数値解法を選択しなくてはいけません。
以下の書籍は、値段が高いですが有限体積法をメインに数値解法がとても詳しく解説されています。
Follow @t_kun_kamakiri
いつもためになる記事を載せてくださりありがとうございます。これらの記事を自分自身の勉強で参考にさせていただいてます。
ところで、第14回以降のpython流体の数値計算はいつ頃アップロードされるのですか？
ものすごく楽しみにしています。
コメントありがとうございます。
週一のペースでアップしています。
本日アップしましたので、是非お読みください(..)_
https://takun-physics.net/10130/