こんにちは(@t_kun_kamakiri)(^^)/
前回では、「内積(スカラー積)」についての記事をまとめました。
今回も引き続き、高校生で習うベクトルについて復習をしておきましょう。
- 外積(ベクトル積)
- 外積の物理での例
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
ベクトルにはスカラー積とベクトル積がある
2つの線形独立な任意のベクトル$\boldsymbol{a}$と$\boldsymbol{b}$に対して、積を考えるとき、次の2つの積があります。
- 内積(スカラー積):$\boldsymbol{a}\cdot \boldsymbol{b}$
- 外積(ベクトル積):$\boldsymbol{a}\times \boldsymbol{b}$
高校生の範囲では、内積は習うでしょうか。
でも、外積はほとんどの高校生が履修単元に入っておらず大学ではじめて学ぶか、気の利かせた高校の先生がこっそり「便利だから・・・」と教えている場合もあります。
ともかく、内積は習うとしても、外積は習っていない可能性があるので詳しく解説をしておおきます。
では、外積の解説をします(^^)/
外積(ベクトル積)
2つの線形独立な任意のベクトル$\boldsymbol{a}$と$\boldsymbol{b}$に対して、積を考えるとき、外積は以下のように定義されます。
※線形独立とは、$\boldsymbol{a}$と$\boldsymbol{b}$が違う方向を向いている場合と考えておけば良いでしょう。
($\boldsymbol{a}=c\boldsymbol{b}$だと互いに向きは同じなので、線形独立ではなりません。)
外積(ベクトル積)
\boldsymbol{a}\times \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\sin\theta\tag{1}
\end{align*}
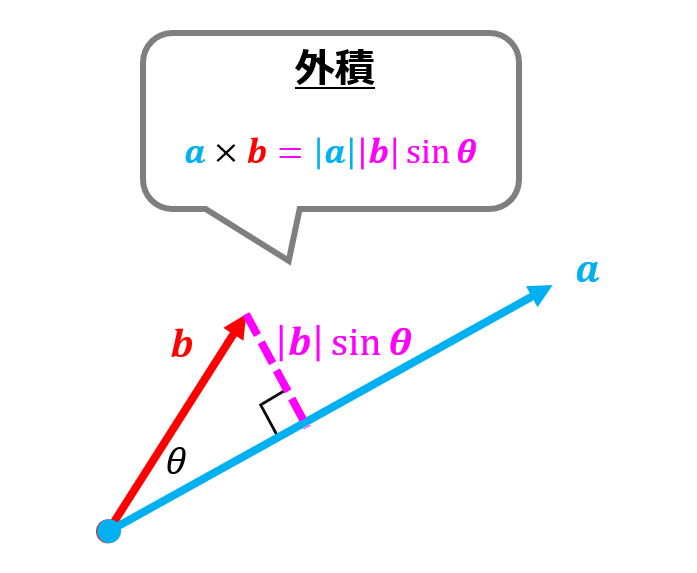
外積は2つのベクトルのうちもう一つが垂直になるような向きに分解して大きさを計算することができます。
\boldsymbol{a}\times \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\sin\theta
\end{align*}
強調しておきますが、これは大きさが$|a|\,|b|\sin\theta$という結果になったということです。
外積はベクトル積と呼ばれているように外積の結果はベクトルになっているため「外積の結果は大きさと向き」があります。
では、向きはどうなっているのか?
3次元の絵を描いて説明します。
2つのベクトル$\boldsymbol{a},\boldsymbol{b}$で張られる平面を考えます。
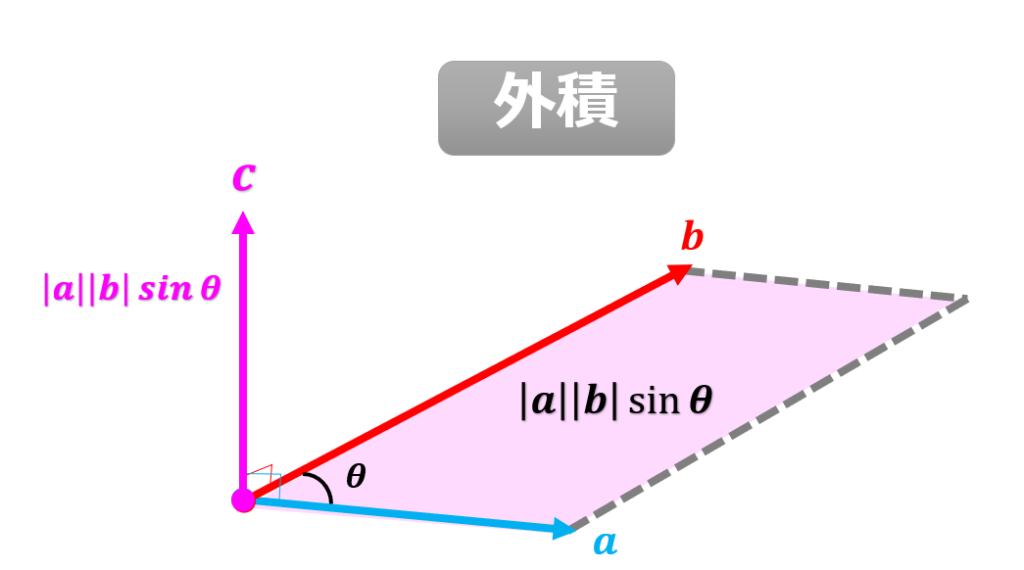
$\boldsymbol{a}\times \boldsymbol{b}=\boldsymbol{c}$とすると、$\boldsymbol{c}$は$\boldsymbol{a}$と $\boldsymbol{b}$で張られる平面に垂直な方向になります。
そして、$\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\sin\theta$は$\boldsymbol{a},\boldsymbol{b}$で作られる面積です。
ここで、大事なことをまとめておきましょう。
$\boldsymbol{c}=\boldsymbol{a}\times \boldsymbol{b}$で定義される外積の結果、
- 大きさ:$|a|\,|b|\sin\theta$
- 方向:$\boldsymbol{a},\boldsymbol{b}$に垂直方向
$\boldsymbol{a}\times \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\sin\theta$の結果は$\boldsymbol{a},\boldsymbol{b}$で作られる面積
しかし、上のようなわかりやすい例なら$\boldsymbol{c}$の向きはわかるかもしれませんが、絵を45°書いてさせたらもうお手上げという人も多いかと思います。
なので、しっかりベクトル積の結果の方向を理解しておく必要があります。
ベクトル積の方向:「右ねじの法則」
ベクトル積は「右ねじの法則」と覚えよう!
右ねじの法則って何かというと以下のような手順を行うことにより、外積の結果の方向を知ることができる方法のことです。
まず右手を出して
- $\boldsymbol{a}$方向に向けます。
- その状態$\boldsymbol{b}$方向に親指以外の4本の指を折り曲げます。
- 親指が向いた方向が$\boldsymbol{c}=\boldsymbol{a}\times\boldsymbol{b}$の方向になります。
絵で描くと↓こんな感じ。
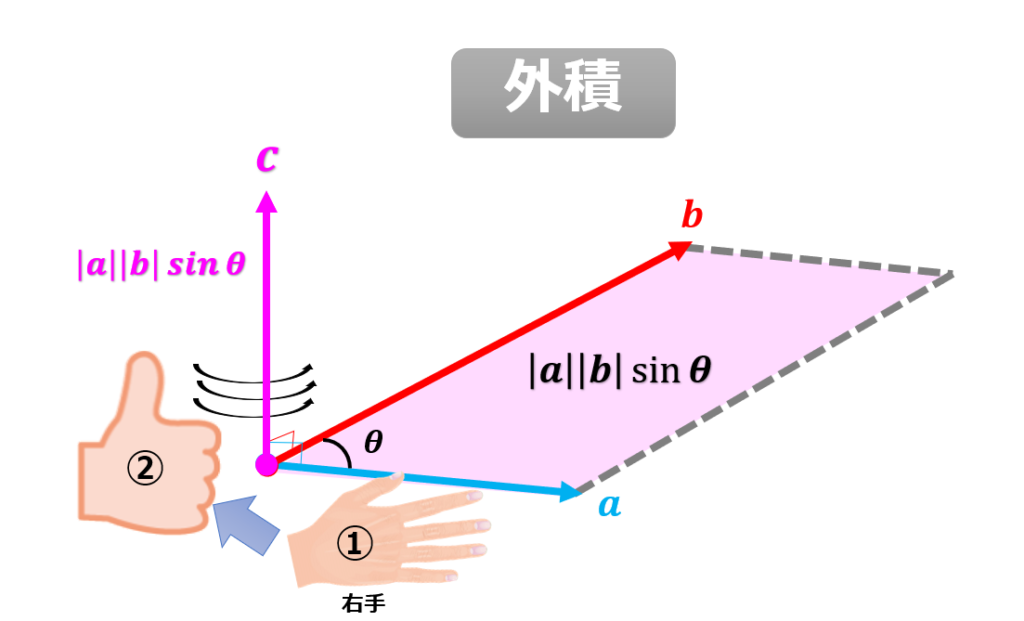
右ねじの法則は、中学生で習う電磁誘導での磁界の向きや、電磁気力(電流、磁界、電磁気力)の方向を示すときに示すものですが、元々の概念は外積からから来ているわけです。
なので、右ねじの法則として外積の方向を覚えておくと便利です。
外積の「大きさと方向」についての理解が得られたところで具体的な外積の計算方法をいくつか紹介しましょう(^^)/
外積の計算方法
外積計算は内積計算と違ってちょっと厄介だなと感じている人が多いかと思います。
そこで、ここでは外積計算の方法を3つほど紹介します。
僕が外積計算をするときは、「1.べクトルの要素をクロスさせて計算」という方法でほとんど済ませています。
具体的な計算をするときは3次元計算までなので1番の方法だけ覚えておけばよいかと思いますが、もっとスマートに記述したい場合や変数が多くなった場合には「3.エディントンンのイプシロン$\varepsilon_{ijk}$を使う」という方法が良いです。
が・・・・慣れないと扱いづらいです。材料力学や流体力学、相対性理論などではしばしば出てくるので今のうちに慣れておくのもよいでしょうね。
ベクトルの要素をクロスさせて計算
個人的に一番使う外積計算の方法ですかね。
高校生の時に学校の先生に教わった記憶があって、それ以来ずっと使っています。
2つのベクトルの成分をクロスしてもうひとつの成分に書くという方法です。
絵を使って説明した方がわかりやすいので↓こちらを見てください。
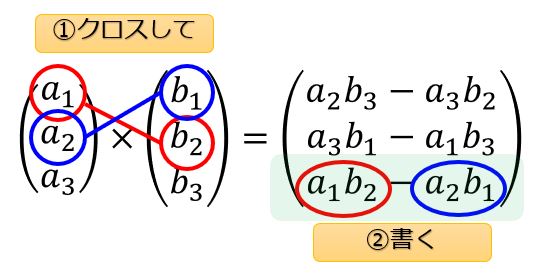

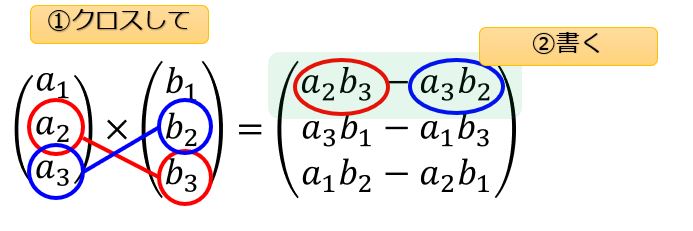
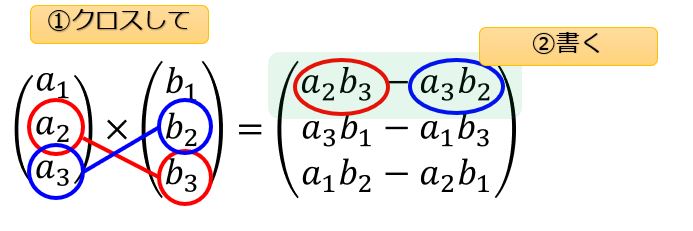
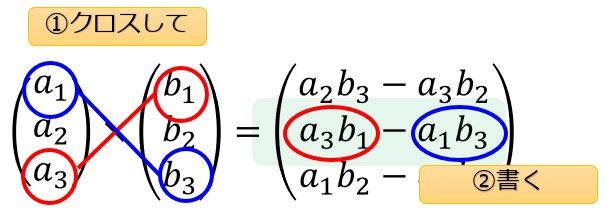

まとめると、
$$
\boldsymbol{a}\times\boldsymbol{b}=\begin{pmatrix}
a_{2}b_{3}-a_{3}b_{2}\\\
a_{3}b_{1}-a_{1}b_{3}\\\
a_{1}b_{2}-a_{2}b_{1}
\end{pmatrix}\tag{2}
$$
となります。
別の参考書を見ていると、以下のようにベクトル積を定義していることもあるので合わせて覚えておくとよいでしょう。
ベクトル積の定義に従って計算する
$\boldsymbol{a}$と$\boldsymbol{b}$を単位ベクトル$\boldsymbol{e}_{1},\boldsymbol{e}_{2},\boldsymbol{e}_{3}$以下のように書きます。
\boldsymbol{a}&=a_{1}\boldsymbol{e}_{1}+a_{2}\boldsymbol{e}_{2}+a_{3}\boldsymbol{e}_{3}\\\
\boldsymbol{b}&=b_{1}\boldsymbol{e}_{1}+b_{2}\boldsymbol{e}_{2}+b_{3}\boldsymbol{e}_{3}
\end{align}
単位ベクトルは、
\boldsymbol{e}_{1} = \begin{pmatrix} 1 \\ 0\\ 0 \end{pmatrix},
\boldsymbol{e}_{2} = \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix},
\boldsymbol{e}_{3} = \begin{pmatrix} 0 \\ 0\\ 1 \end{pmatrix}
\end{align*}
内積計算のときは、$\boldsymbol{e}_{i}\cdot\boldsymbol{e}_{2}=\delta _{ij}$と定義していましたが、外積の場合は以下のように定義します。
\boldsymbol{e}_{i}\times\boldsymbol{e}_{j}=\boldsymbol{e}_{k}\tag{4}
\end{align*}
これを具体的に書くと、
となります。
外積の場合は注意が必要で一般的には交換に関しては可換ではありません。$\boldsymbol{e}_{i}\times\boldsymbol{e}_{j}\neq \boldsymbol{e}_{j}\times\boldsymbol{e}_{i}$です。
ただし、
- 順序を入れ替えればマイナス倍になるだけ:$\boldsymbol{e}_{j}\times\boldsymbol{e}_{i}=-\boldsymbol{e}_{k}$
- 同じベクトル方向の場合は0:$\boldsymbol{e}_{i}\times\boldsymbol{e}_{i}=0$
となります。
これを用いると、外積計算は・・・
\boldsymbol{a}\times\boldsymbol{b}&=(a_{1}\boldsymbol{e}_{1}+a_{2}\boldsymbol{e}_{2}+a_{3}\boldsymbol{e}_{3})\times (b_{1}\boldsymbol{e}_{1}+b_{2}\boldsymbol{e}_{2}+b_{3}\boldsymbol{e}_{3})\\
&=a_{1}b_{1}\boldsymbol{e}_{1}\times\boldsymbol{e}_{1}+a_{1}b_{2}\boldsymbol{e}_{1}\times\boldsymbol{e}_{2}+a_{1}b_{3}\boldsymbol{e}_{1}\times\boldsymbol{e}_{3}\\
&+a_{2}b_{1}\boldsymbol{e}_{2}\times\boldsymbol{e}_{1}+a_{2}b_{2}\boldsymbol{e}_{2}\times\boldsymbol{e}_{2}+a_{2}b_{3}\boldsymbol{e}_{2}\times\boldsymbol{e}_{3}\\
&+a_{3}b_{1}\boldsymbol{e}_{3}\times\boldsymbol{e}_{1}+a_{3}b_{2}\boldsymbol{e}_{3}\times\boldsymbol{e}_{2}+a_{3}b_{3}\boldsymbol{e}_{3}\times\boldsymbol{e}_{3}\\
&=(a_{2}b_{3}-a_{3}b_{2})\boldsymbol{e}_{1}+(a_{3}b_{1}-a_{1}b_{3})\boldsymbol{e}_{2}+(a_{1}b_{2}-a_{2}b_{1})\boldsymbol{e}_{3}\tag{4}
\end{align*}
まとめると、
\boldsymbol{a}\times\boldsymbol{b}=\begin{pmatrix}
a_{2}b_{3}-a_{3}b_{2}\\
a_{3}b_{1}-a_{1}b_{3}\\
a_{1}b_{2}-a_{2}b_{1}
\end{pmatrix}\tag{2}
\end{align*}
となります。
エディントンのイプシロン$\varepsilon_{ijk}$を使う
エディントンのイプシロンのルールを説明する必要があります。
$i,j,k$が1,2,3のいずれかをとれるとします。
そして、エディントンのイプシロンは以下のように定義されています。
\varepsilon_{ijk}=\left\{\begin{matrix}
1\,\,\,(i,j, k)&=(1,2,3),(2,3,1),(3,1,2)\\
-1 \,\,\,(i,j, k)&=(1,3,2),(3,2,1),(2,1,3)\\
0\,\,\,(other)&
\end{matrix}\right.
\end{align*}
$\varepsilon_{ijk}$をレビチビタ記号と呼びます。
具体的には以下のようになっています。
$(i,j,k)$の入れ替えの組は${}_3 P_2=6$通りあり以下のようになっています。
- 入れ替えに対して偶数回の場合:$\varepsilon_{123}=\epsilon_{231}=\varepsilon_{312}=1$
- 入れ替えに対して奇数回の場合:$\varepsilon_{132}=\varepsilon_{321}=\varepsilon_{213}=-1$
どおなっているのか確認をしてみましょう。
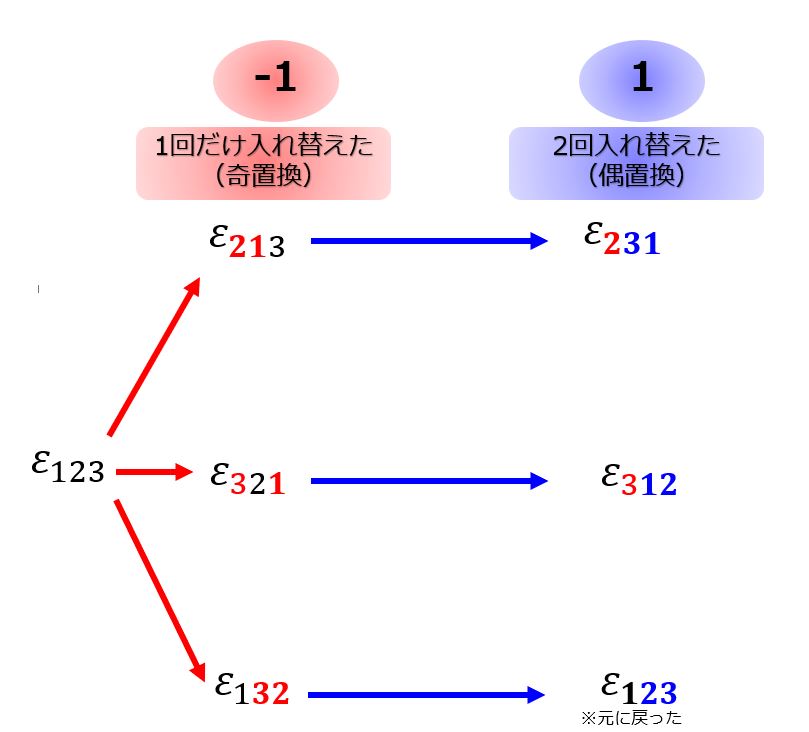

「奇置換」や「偶置換」は添え字の入れ替えの回数を意味しています。
- 奇数回の入れ替えの場合は-1
- 偶数回の入れ替えの場合は+1
ということです。
さらに同じ添え字がある場合はゼロということですね。
例:\(\varepsilon_{112}=\varepsilon_{211}=0\)など・・・
このルールを適用して外積計算を定義します。
\boldsymbol{a}\times\boldsymbol{b}=\varepsilon_{ijk}a_{j}b_{k}\tag{5}
\end{align*}
となります。
ただし、同じ添え字がある場合は和をとることになります(アインシュタインの縮約といいます)
先ほどのルールを適用して式を展開してみましょう。
$j$と$kの添え字がそれぞれ2つあるため和をとる必要があります。
- $i=1$の場合、
(\boldsymbol{a}\times\boldsymbol{b})_{1}&=\varepsilon_{111}a_{1}b_{1}+\varepsilon_{112}a_{1}b_{2}+\varepsilon_{113}a_{1}b_{3}\\
&+\varepsilon_{121}a_{2}b_{1}+\varepsilon_{122}a_{2}b_{2}+\varepsilon_{123}a_{2}b_{3}\\
&+\varepsilon_{131}a_{3}b_{1}+\varepsilon_{132}a_{3}b_{2}+\varepsilon_{133}a_{3}b_{3}\\
&=\varepsilon_{123}a_{2}b_{3}+\varepsilon_{132}a_{3}b_{2}\\
&=a_{2}b_{3}-a_{3}b_{2}
\end{align*}
- $i=2$の場合、
(\boldsymbol{a}\times\boldsymbol{b})_{2}&=\varepsilon_{211}a_{1}b_{1}+\varepsilon_{212}a_{1}b_{2}+\varepsilon_{213}a_{1}b_{3}\\
&+\varepsilon_{221}a_{2}b_{1}+\varepsilon_{222}a_{2}b_{2}+\varepsilon_{223}a_{2}b_{3}\\
&+\varepsilon_{231}a_{3}b_{1}+\varepsilon_{232}a_{3}b_{2}+\varepsilon_{233}a_{3}b_{3}\\
&=\varepsilon_{213}a_{1}b_{3}+\varepsilon_{231}a_{3}b_{1}\\
&=-a_{1}b_{3}+a_{3}b_{1}
\end{align*}
- $i=3$の場合、
(\boldsymbol{a}\times\boldsymbol{b})_{3}&=\varepsilon_{311}a_{1}b_{1}+\varepsilon_{312}a_{1}b_{2}+\varepsilon_{313}a_{1}b_{3}\\
&+\varepsilon_{321}a_{2}b_{1}+\varepsilon_{322}a_{2}b_{2}+\varepsilon_{323}a_{2}b_{3}\\
&+\varepsilon_{331}a_{3}b_{1}+\varepsilon_{332}a_{3}b_{2}+\varepsilon_{333}a_{3}b_{3}\\
&=\varepsilon_{312}a_{1}b_{2}+\varepsilon_{321}a_{2}b_{1}\\
&=a_{1}b_{2}-a_{2}b_{1}
\end{align*}
丁寧に計算をしてみました。
まとめると、
\boldsymbol{a}\times\boldsymbol{b}=\begin{pmatrix}
a_{2}b_{3}-a_{3}b_{2}\\
a_{3}b_{1}-a_{1}b_{3}\\
a_{1}b_{2}-a_{2}b_{1}
\end{pmatrix}
\end{align*}
となります。
エディントンのイプシロンを使った公式はまだありますが、はじめは外積計算くらいで慣れておくとよいです。
もっと複雑な外積計算(例えばベクトル3重積)などでは威力を発揮します。
行列式のサラス公式を使う方法
これは行列式を習っている人向けの解説ですので、行列式を理解してから思い出してもらえれば良いです。
3次正方行列(サラスの公式)の計算は以下のようにします。
3次正方行列$A=\begin{pmatrix}
a_{11} &a_{12} & a_{13} \\
a_{21} &a_{22} & a_{23} \\
a_{31} &a_{32} & a_{33} \tag{3}
\end{pmatrix}\\$の行列式を考えましょう。
3次の正方行列の行列式の計算にはサラスの公式というとても便利な公式があります。
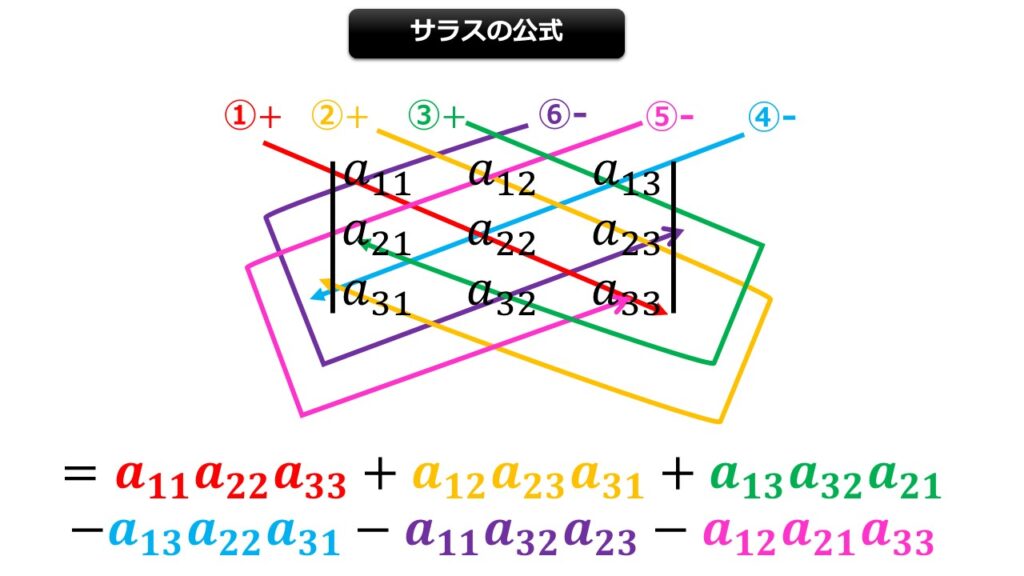

上の絵を見ながら計算を行えば3次正方行列に対しても行列式が計算できます。
|A|&=\begin{vmatrix}
a_{11} &a_{12} & a_{13} \\
a_{21} &a_{22} & a_{23} \\
a_{31} &a_{32} & a_{33} \\
\end{vmatrix}\\
&=\begin{vmatrix}
a_{11} &a_{12} & a_{13} \\
a_{21} &a_{22} & a_{23} \\
a_{31} &a_{32} & a_{33} \\
\end{vmatrix}\\
&=a_{11} a_{22} a_{33}+a_{12} a_{23}a_{31}+a_{13}a_{32}a_{21}\\
&-a_{13}a_{22} a_{31}-a_{11}a_{32} a_{23} -a_{13}a_{21}a_{33}
\end{align*}
「3つの要素を掛け算して3回足して、次に3つの要素を掛け算して3回引く」という要領で計算を行います。
これを使って
\boldsymbol{a}\times \boldsymbol{b}&=\begin{vmatrix}
\boldsymbol{e}_{1} &\boldsymbol{e}_{2} & \boldsymbol{e}_{3} \\
a_{1} &a_{2} & a_{3} \\
b_{1} &b_{2} & b_{3} \\
\end{vmatrix}\\
&=\boldsymbol{e}_{1} a_{2} b_{3}+\boldsymbol{e}_{2} a_{3}b_{1}+\boldsymbol{e}_{3}b_{2}a_{1}\\
&-\boldsymbol{e}_{3}a_{2} b_{1}-\boldsymbol{e}_{1}b_{2} a_{3} -\boldsymbol{e}_{2}a_{1}b_{3}\\
&=(a_{2}b_{3}-a_{3}b_{2})\boldsymbol{e}_{1}+(a_{3}b_{1}-a_{1}b_{3})\boldsymbol{e}_{2}+(a_{1}b_{2}-a_{2}b_{1})\boldsymbol{e}_{3}
\end{align*}
計算できます。
外積の物理の例:モーメント、面積速度、ローレンツ力
ここからは外積計算が行われる例を3つ見ておきます。
- モーメント
- 面積速度
- ローレンツ力
モーメント
モーメントは力学の分野で出てきますね。
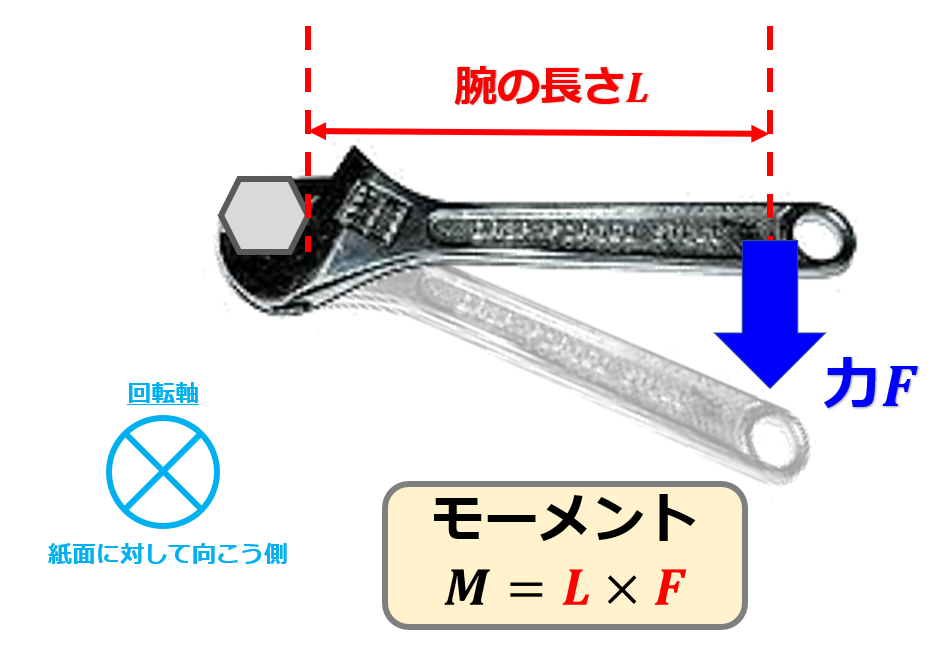

腕の長さ$L$に対して、腕の長さに垂直な方向に力$F$を加えます。
このときのモーメントは、
\boldsymbol{M}=\boldsymbol{L}\times\boldsymbol{F}\tag{6}
\end{align*}
ベクトルの向きは右ねじの法則から紙面に対して向こう側です。
面積速度一定
面積速度一定とは「惑星と太陽とを結ぶ線分が単位時間に描く面積は一定である。」というケプラーの第二法則です。
絵に描くと↓こんな感じです。
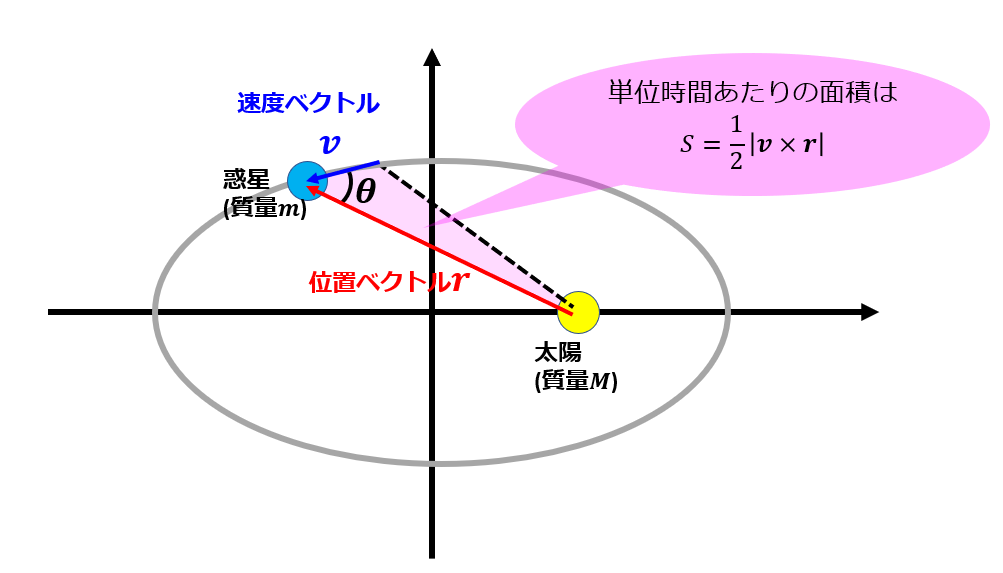

惑星が単位時間あたりに進む距離は速度ベクトル\(\boldsymbol{v}\)で表すことができ、惑星と太陽の相対ベクトルは位置ベクトルで表すことができます。
このとき、
h=\frac{1}{2}|\boldsymbol{r}\times\boldsymbol{v}|=const\tag{7}
\end{align*}
であることが知られています。
ここから以下の2点が言えます。
- $\boldsymbol{r}\times\boldsymbol{v}=const$であることから、太陽と惑星の軌道は平面上の運動に限られる。
- $m\boldsymbol{r}\times\boldsymbol{v}=const$とも言える。
これは惑星の角運動量が保存していることを意味している。
ここでは、惑星運動の詳細は話す余裕がないですが、外積計算は惑星の運動において使われるということを覚えておいてもらえればよいでしょう(^^)/
ローレンツ力
ローレンツ力と電磁気力でも外積が使われます。
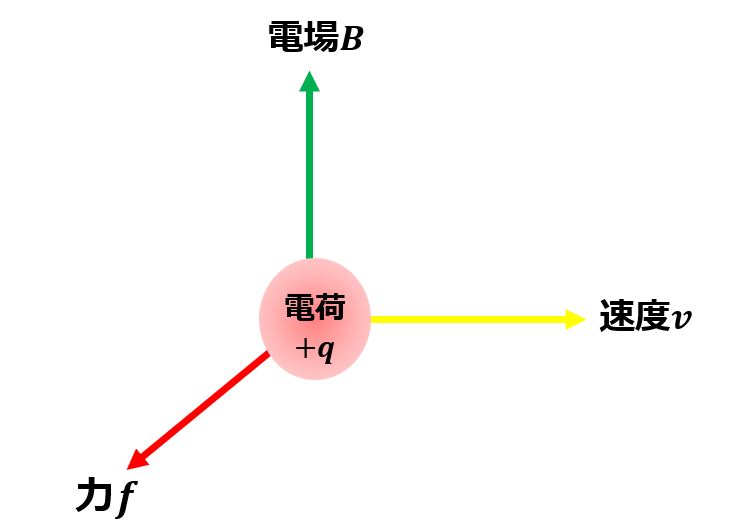
まずローレンツ力は、電場$\boldsymbol{B}$の中を単位電荷$q$が速度$\boldsymbol{v}$で動いているとき、
\boldsymbol{f}=q\boldsymbol{v}\times\boldsymbol{B}\tag{8}
\end{align*}
のローレンツ力が働きます。

電磁気力
電場$\boldsymbol{B}$の中を長さ$l$の棒に電流$I$が流れているとき、電磁力もローレンツ力と同様に以下の外積で表すことができます。
\boldsymbol{F}=l\boldsymbol{I}\times\boldsymbol{B}\tag{9}
\end{align*}
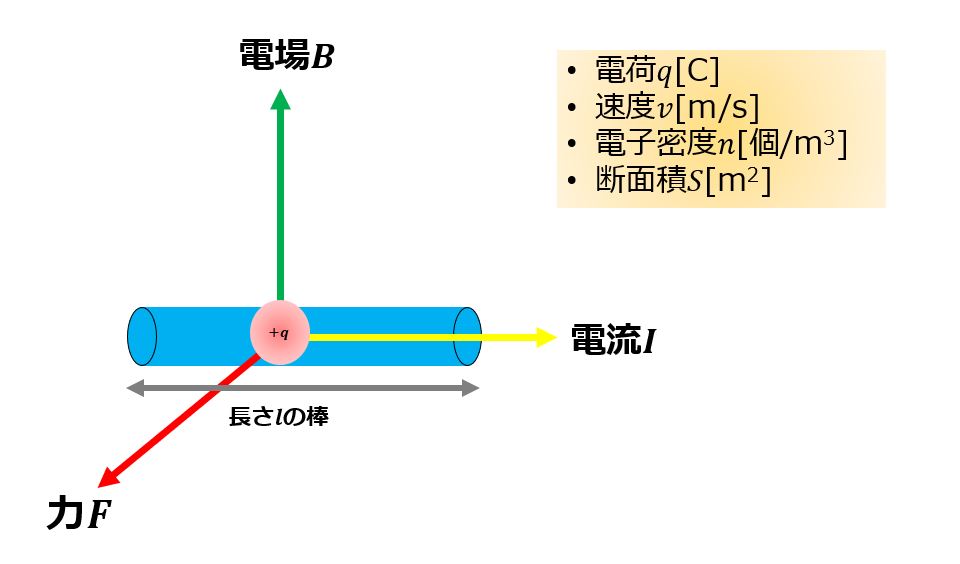

ところで、ローレンツ力と電磁気力って何が違うか?
- ローレンツ力:単位電荷あたりに働く力
- 電磁気力:単位電荷あたりに働く力の総和
電流は単位時間当たりの電荷量なので、$I=\frac{dQ}{dt}=\frac{d(qnxS)}{dt}=qn\frac{d(x)}{dt}=qnSv$となります。
電磁力は、
\boldsymbol{F}=qnSl\boldsymbol{v}\times\boldsymbol{B}\tag{10}
\end{align*}
となります。
ところで、$nSl$が長さ$l$内の電荷の数の総和であることから(10)を$nSl$で割ると、
\boldsymbol{f}=\frac{F}{nSl}=q\boldsymbol{v}\times\boldsymbol{B}\tag{11}
\end{align*}
ローレンツ力になります。
まとめ
外積についての解説を行いました。
外積(ベクトル積)
\boldsymbol{a}\times \boldsymbol{b}=\left |\boldsymbol{a}\right|\left |\boldsymbol{b}\right|\sin\theta\tag{1}
\end{align*}
本記事では、外積計算の方法を3つほど紹介しました。
外積は物理の中でもたくさん出てきますが、本記事では以下の外積が使われる例を3つ紹介しています。
- モーメント
- 面積速度
- ローレンツ力
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/