こんにちは(@t_kun_kamakiri)(^^)/
前回では、「外積(ベクトル積)」についての記事をまとめました。
今回は行列について解説を行います。
- 行列の定義
- 行列の基本的な考え方
- 行列の計算方法
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事を読むと行列の計算方法がよくわかることでしょう!
行列の定義
まずは行列の定義からです。
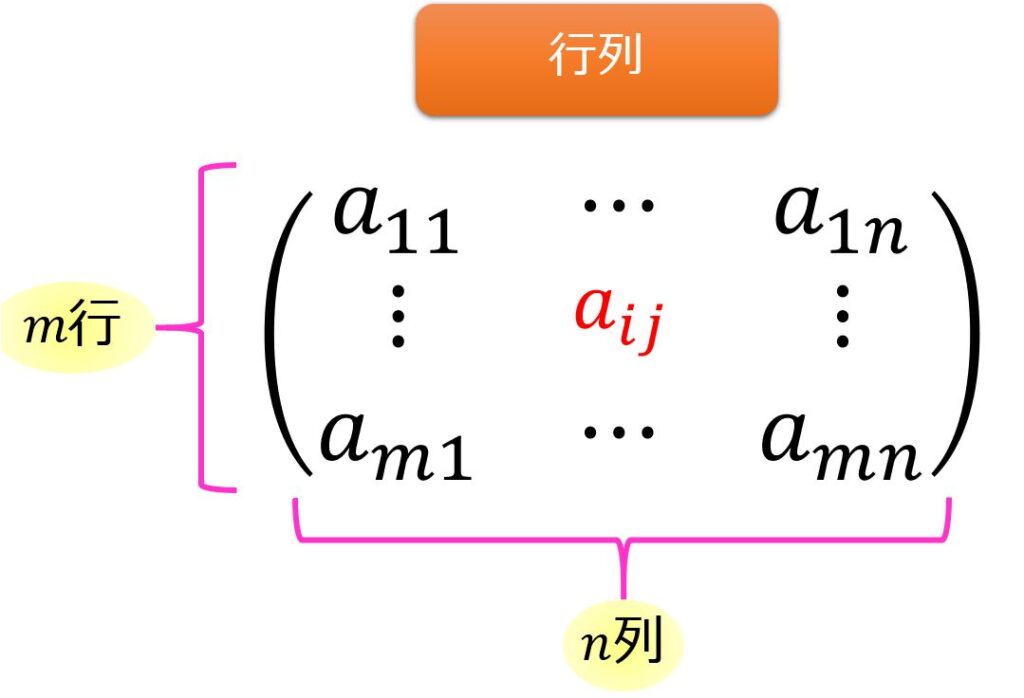
行列とは「自然数$m,n$に対して、$m\times n$個の複素数$a_{ij}$を縦に$m$個、横に$n$個並べた$(m,n)$の表」のことをいう。
実際に行列を書いてみましょう。

もう少し具体的に書いてみましょうか。
簡単な場合を考えるため$(2\times 2)$(2行2列)の行列を考えてみましょう。
特に「あれ?どっちが行で、どっちが列だったかな」と思ったときはこちらの行列という字から「行と列」を思い出してください。
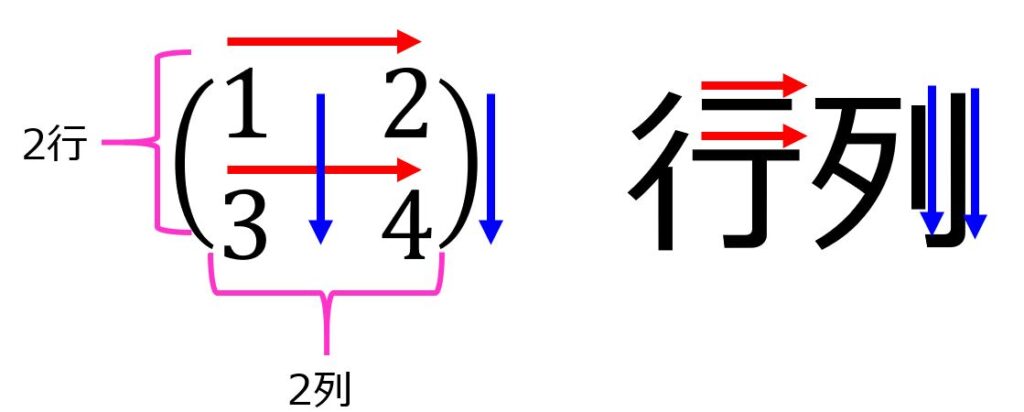

行列にいまいち慣れないという方は以下のような表を()でまとめたと考えてもよいでしょう。
(例)クラス内の5人の「身長、体重、性別、成績」を表にする。
表にしたものを行列表記にすると以下のようになります。
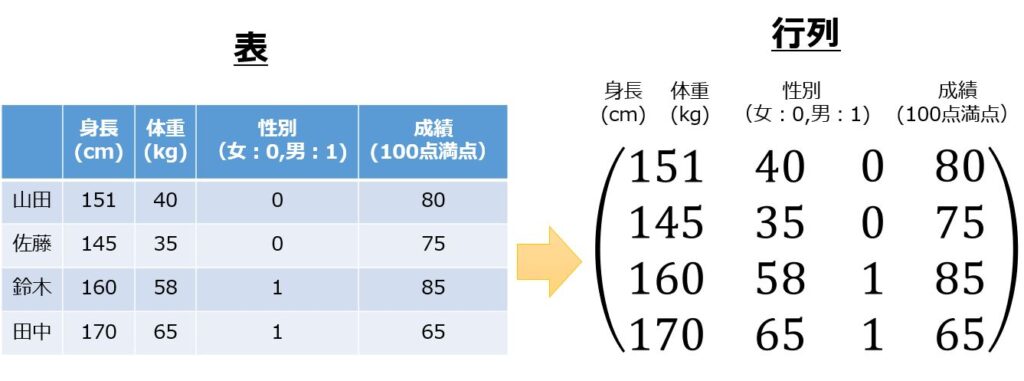

行列の用途や利点は後ほど学びます。
ここでは、行列のイメージが表であることがわかれば良いです。
行列の成分
行列の中の中の「上から数えて$i$行目、左から数えて$j$列目」の$(i,j)$成分を$a_{ij}$成分と言います。
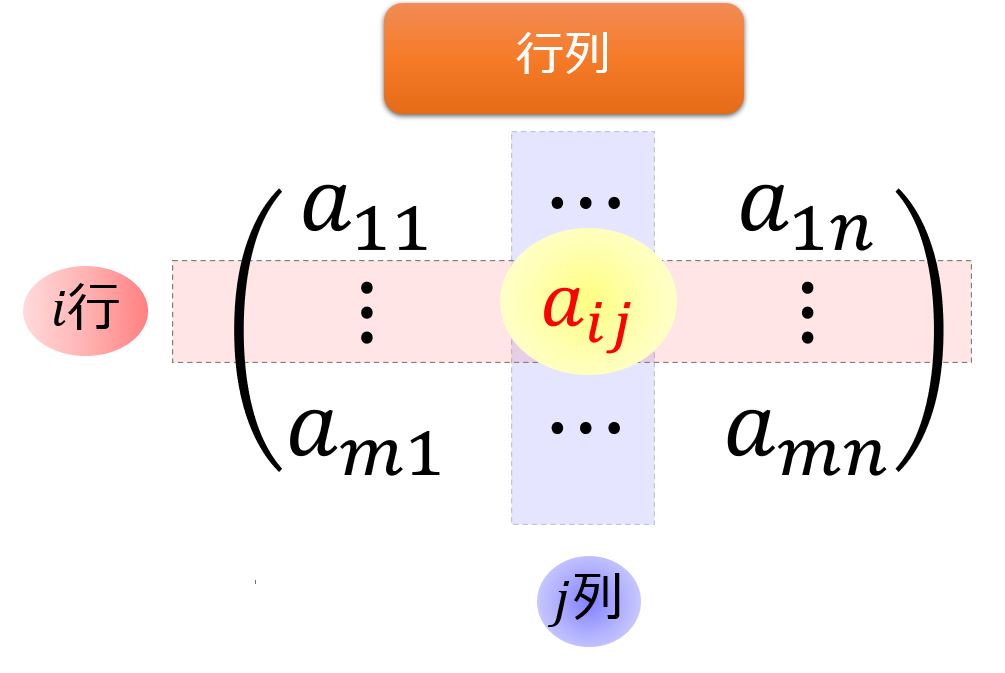

わかりやすく具体例を出すと以下のような「2行2列」の行列があった場合、1行2列目である$(1,2)$成分は$a_{12}=2$となります。


では、以下で具体的な行列の計算方法を見ていきましょう。
行列の計算方法
行列の演算について特に重要なのは行列の掛け算です。
一般的な数における掛け算は$ab=ba$が成り立ちますのでどちらから数を掛けようが結果は変わらないのです。
でも、行列の計算の掛け算の順番はかなり丁寧に意識をする必要があります。
なぜなら一般的に2つの行列の掛け算のは、掛け算の順番の入れ替えに対して等しいとは限らないからです。
AB\neq BA\end{align*}
では、具体的に行列の掛け算方法を示します。
2つの2行2列の行列$A=\begin{pmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{pmatrix}$、$B=\begin{pmatrix}
b_{11} & b_{12}\\
b_{21} & b_{22}
\end{pmatrix}$を用意します。
AとBの2つの行列の掛け算は以下のように計算を行います。
丁寧に計算を載せておきます。
1行1列目の結果
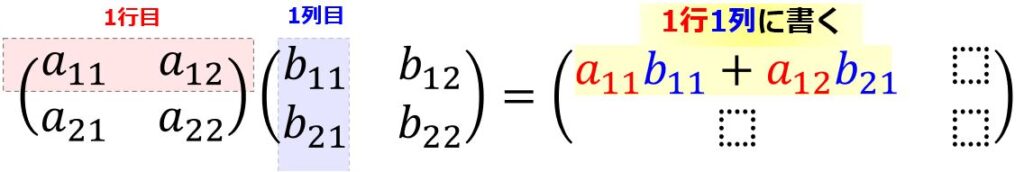
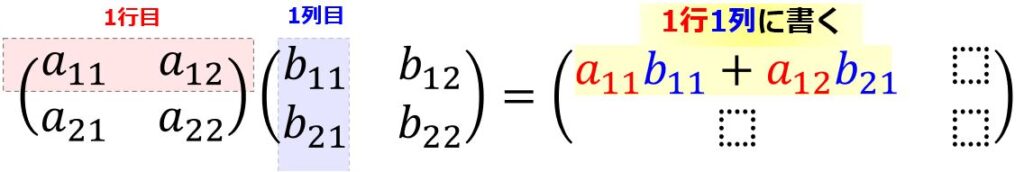
2行1列目の結果
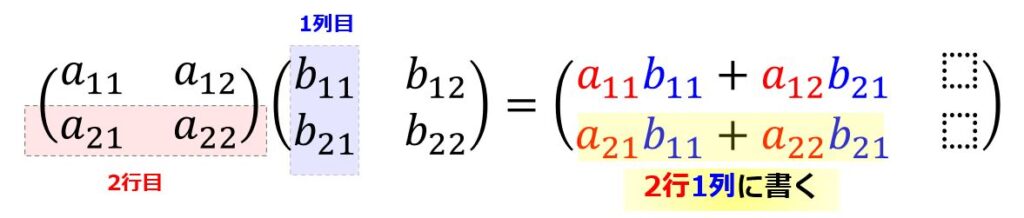
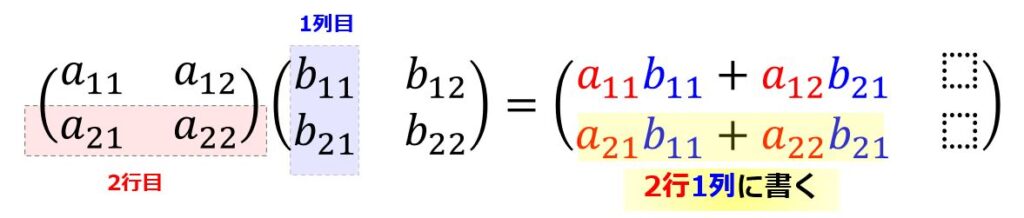
1行2列目の結果
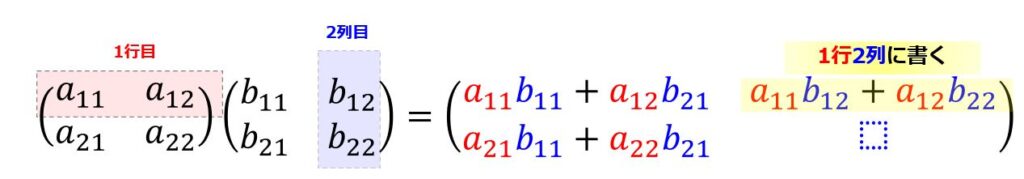
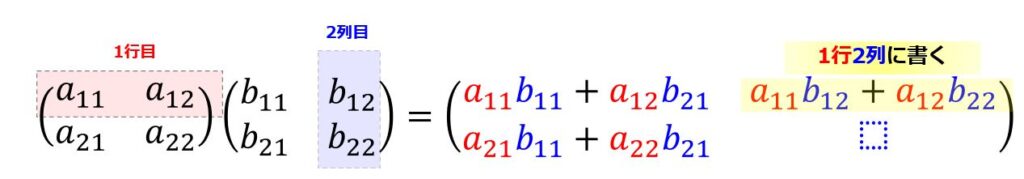
2行2列目の結果
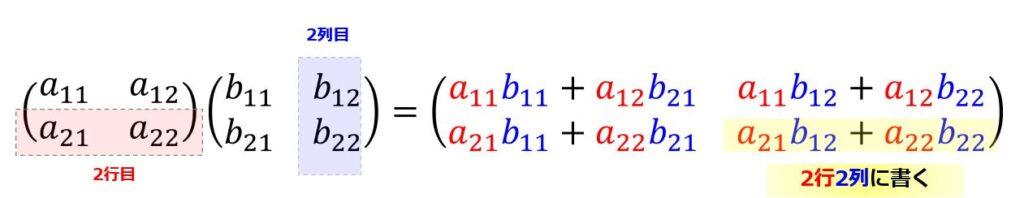
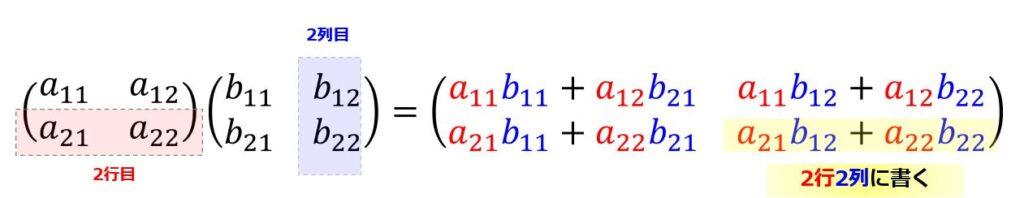
なので最終的な結果は、
AB&=\begin{pmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{pmatrix}\begin{pmatrix}
b_{11} & b_{12}\\
b_{21} & b_{22}
\end{pmatrix}\\
&=\begin{pmatrix}
a_{11}b_{11} +a_{12}b_{21}& a_{11}b_{12} +a_{12}b_{22}\\
a_{21}b_{11} +a_{22}b_{21} & a_{21}b_{12} +a_{22}b_{22}
\end{pmatrix}
\end{align*}
文字だとイメージがつかないかもしれないので具体的な計算もしてみましょう。
$A=\begin{pmatrix}
1 & 2\\
3 & 4
\end{pmatrix}$と$B=\begin{pmatrix}
5 & 6\\
7 & 8
\end{pmatrix}$に対する行列の掛け算は、
AB&=\begin{pmatrix}
1 & 2\\
3 & 4
\end{pmatrix}\begin{pmatrix}
5 & 6\\
7 & 8
\end{pmatrix}\\
&=\begin{pmatrix}
1\times 5 +2\times 7& 1\times 6 +2\times 8\\
3\times 5 +4\times 7 & 3\times 6 +4\times 8
\end{pmatrix}\\
&=\begin{pmatrix}
19& 22\\
43 & 50
\end{pmatrix}
\end{align*}
となります。
「2行2列」と「2行2列」とき、行列の掛け算の結果は2行2列になります。
重要なことをまとめると、
このことを以下で一般的な話にまとめておきます。
$A$が$(l,m)$行列、$B$が$(m,k)$行列の掛け算$AB$は$(l,k)$行列になる
一般的な話をすると$A$が$(l,m)$行列、$B$が$(m,k)$行列であるとき、行列の掛け算$AB$は計算できて($m$が同じなので)、結果は$(l,k)$行列になります。
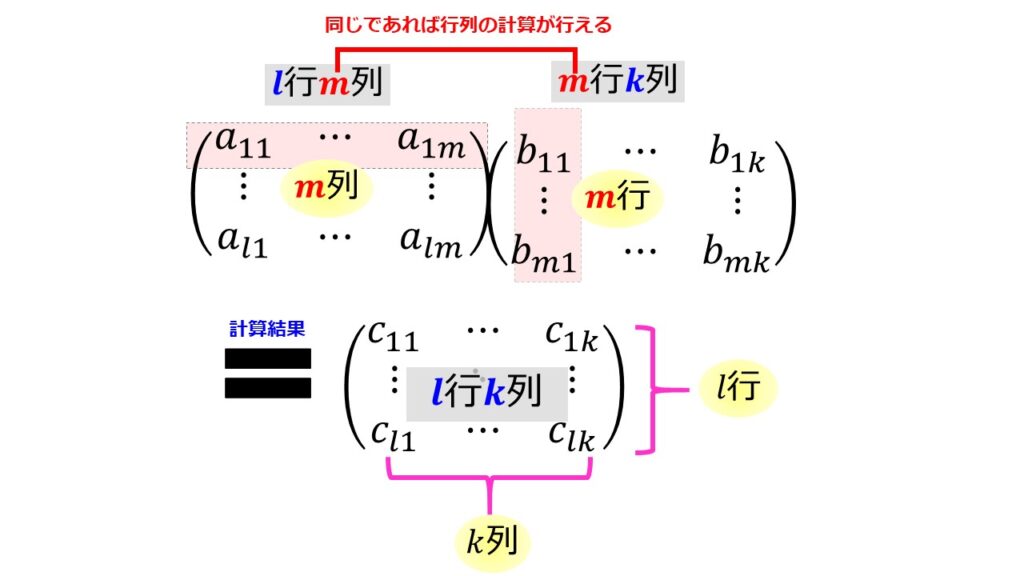

文字だとイメージがつかないかもしれないので具体的な計算もしてみましょう。
2行2列$A=\begin{pmatrix}
1 & 2\\
3 & 4
\end{pmatrix}$と、2行3列$B=\begin{pmatrix}
5 & 6 & 7\\
8 & 9 & 10
\end{pmatrix}$に対する行列の掛け算は、
AB&=\begin{pmatrix}
1 & 2\\
3 & 4
\end{pmatrix}\begin{pmatrix}
5 & 6 & 7\\
8 & 9 & 10
\end{pmatrix}\\
&=\begin{pmatrix}
1\times 5 +2\times 8& 1\times 6 +2\times 9 &1 \times 7 +2\times 10 \\
3\times 5 +4\times 8& 3\times 6 +4\times 9 &3 \times 7 +4\times 10 \\
\end{pmatrix}\\
&=\begin{pmatrix}
21&24 &27 \\
47&54& 61\\
\end{pmatrix}
\end{align*}
計算することができて、結果は2行3列となっていますね。
では、今までのをまとめて行列の掛け算を行った後の要素について書き下すと以下となります。
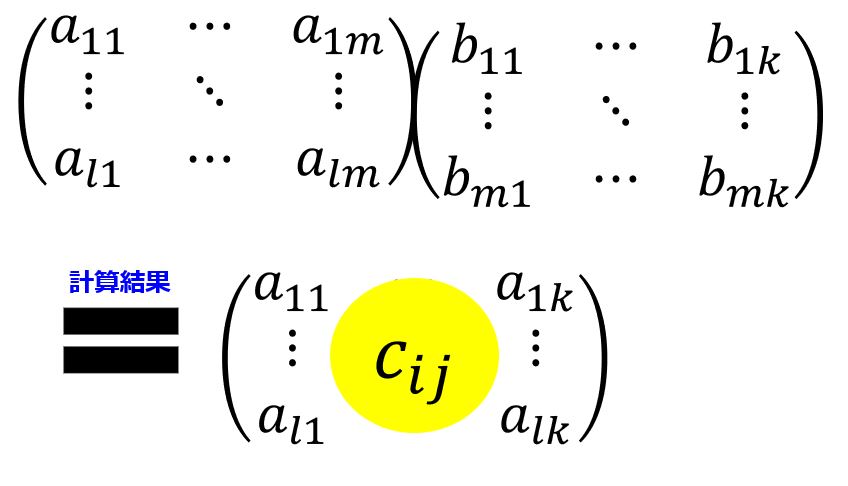

c_{ij}=\sum^{m}_{k=1}a_{ik}b_{kj}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{im}b_{mj}
\end{align*}
以上で行列計算の基本的な内容の解説をしてきました。
あとは行列に対する演算を以下に記してこの記事の内容を終えようと思います_(._.)_
行列に対する演算
本記事では主に行列の掛け算に対する内容でした。
では、行列に対する足し算はどうなるのかというと、とても簡単で以下のように行列の要素の足し算を行列内で行うだけとなります。
2つの2行2列の行列$A=\begin{pmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{pmatrix}$、$B=\begin{pmatrix}
b_{11} & b_{12}\\
b_{21} & b_{22}
\end{pmatrix}$を用意して、足し算を行うと以下となります。
A+B&=\begin{pmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{pmatrix}+\begin{pmatrix}
b_{11} & b_{12}\\
b_{21} & b_{22}
\end{pmatrix}\\
&=\begin{pmatrix}
a_{11}+b_{11} & a_{12}+b_{12}\\
a_{21} +b_{21} &a_{22}+b_{22}
\end{pmatrix}
\end{align*}
各要素の足し算を行うだけですね。
その他の行列に対する演算もまとめておきましょう。
行列の計算と言えど足し算引き算に対してはほとんど数の演算と同じですね。
ただ、本記事の主題である行列の掛け算は注意が必要ですし、何より行列に割り算というのは存在しません。
割り算というのは数$a$に対して$ab=1$となるbが存在するかどうかが重要なのですが、$a÷a=1$と÷記号を使いますが、行列の場合に$A÷A=E(単位行列)$のような書き方はありません。
今後の記事で扱う逆行列で詳しく解説を行います。
まとめ
本記事では行列の定義と行列の計算方法について解説を行いました。
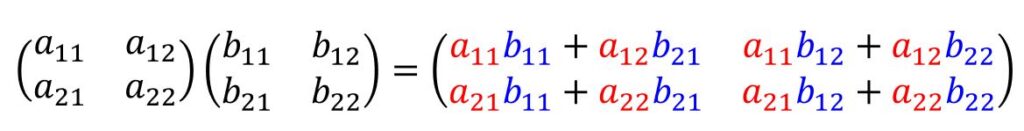
行列の計算方法については、慣れるまで何度も計算演習を積んでください。
また、「$A$が$(l,m)$行列、$B$が$(m,k)$行列であるとき行列の掛け算$AB$は計算できて($m$が同じなので)、結果は$(l,k)$行列になる」といのも重要なことです。
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/