どうも(^^)/
本記事
今までブログに書いた「ラグランジュ方程式の導出」に対する全体像を載せておきます。
関連記事
今まで書いたラグランジュ方程式の導出の記事が下記です。
ラグランジュ方程式の導出は「これ!」といった唯一の方法があるのではなく色々な角度から導出できます。
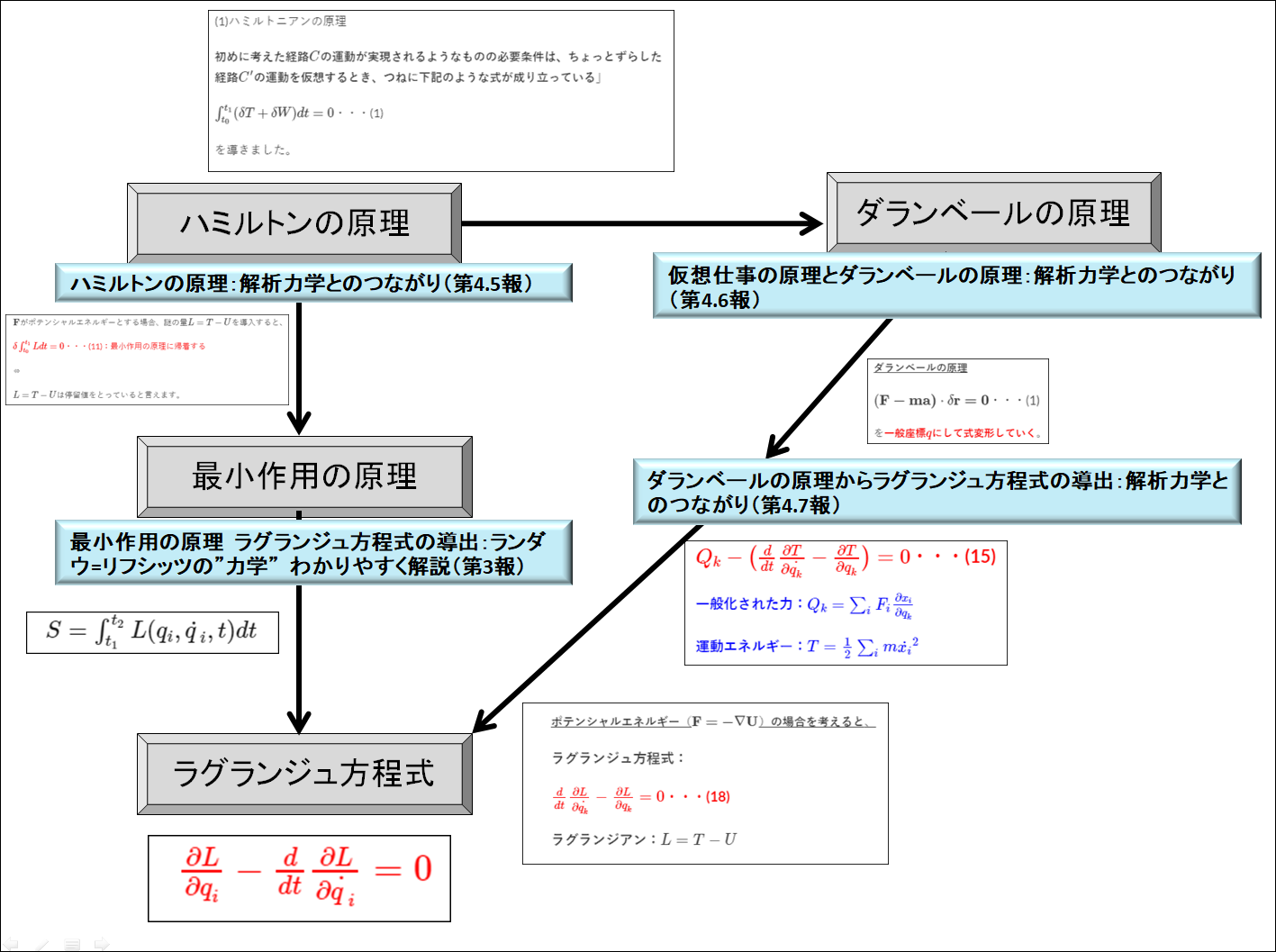
ラグランジュ方程式に関する地図
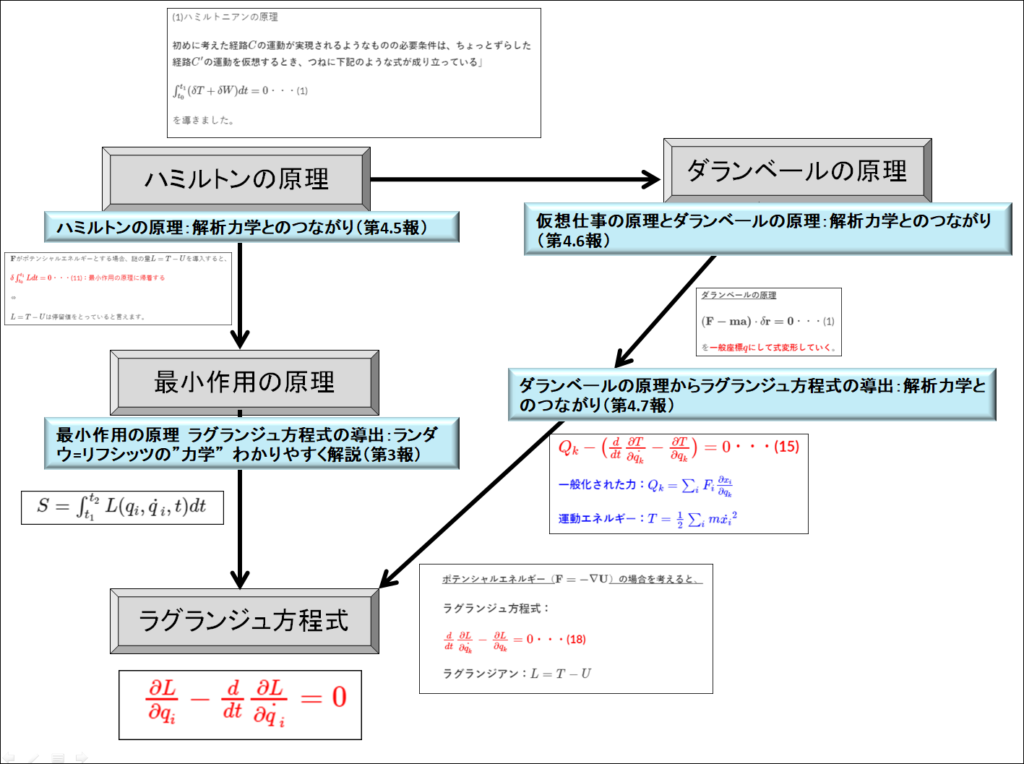
上のフローを見ればお分かりの通り、ラグランジュ方程式は、
とよくわからない量ラグランジアン\(L\)で記述できます。
はじめて解析力学を習う人はこのわけもわからないラグランジアン\(L\)というのを仕方なく受け入れるしかありません。
さらに、\(U\)をポテンシャルエネルギーとして\(L=T-U\)を導入してすると、
なぜか運動方程式\(ma=F\)になるのです。
不思議だな~って思うんです。
自分でも面白いなと思って書いた記事としては、ダランベールの原理を一般座標系に直すとラグランジュ方程式が導出できるという記事です。
ダランベールの原理からラグランジュ方程式の導出:解析力学とのつながり(第4.7報)
やはり、ラグランジュ方程式の本質は>>「最小作用の原理 ラグランジュ方程式の導出:ランダウ=リフシッツの”力学” わかりやすく解説(第3報)」でも書いた通り、
- 最小作用の原理
- 一般座標の導入
この二つに限るのではないかと思います。
この二つだけ見ると、別にニュートンの第二法則(運動方程式)のみならず、
- シュレディンガー方程式(量子力学)
- ナビエストークス方程式(流体力学)
- 相対性理論への拡張も(できるのかな?勉強不足だ・・・)
それぞれに対してラグランジアン\(L\)さえわかっていれば座標系によらない一般的な記述を可能にするのではないかと考えられるわけですね。
便利であります(^^)
解析力学のまとめ
解析力学は、「ニュートン力学をより美しく一般的な形式に従って運動を記述できるようにした学問である」
※ニュートン力学のみならずもっと広い意味で一般的な形式を目指した学問とも言えますね!(^^)!
個人的には、ナビエストークス方程式のラグランジアンはあまり見たことないのでどうなるのか知りたいところです。