こんにちは(@t_kun_kamakiri)(^^)/
ブログをはじめたのが2018年の4月からでかれこれ3年半以上ブログを運営していることになります。
ブログからの広告収益は月に1万円弱、6~8万PVといった状況であり多少なりとも社会貢献をしていると感じます。現在は製造業でCAE解析でシミュレーションをメインで仕事をしているのですが、本業以外での収益を得る手段を体験できているのは自分にとってとても大きな収穫です。
「たったの月1万円なの?」と思うかもしれませんが、ブログから収益を得るためには多少なりとも影響力を持たなくてはいけません。
ありがたいことにその影響力もあってか、個別で以下のような相談も来ます。
ブログからのアクセスを集めて自分のしたい仕事を選び、値段も自分で設定できます。
最近あったのは「流体力学の個別レクチャーを受けたい」とのことで今準備をしています_(._.)_
流体力学に関する内容はこちらに記載していますので興味ある方はお読みください。
前置きは長くなりましたが、ブログから個別でお問い合わせいただいた内容に関しての記事を紹介したいと思います。
問題設定は以下となります。
ひもでつながれた2質点があり、質点1と質点2はそれぞれ別の初期速度を持って回転を開始するとします。そのときの運動のシミュレーションを行う。
※ひもにつながれた2つの球体の1つを手に取って投げるといったイメージです。
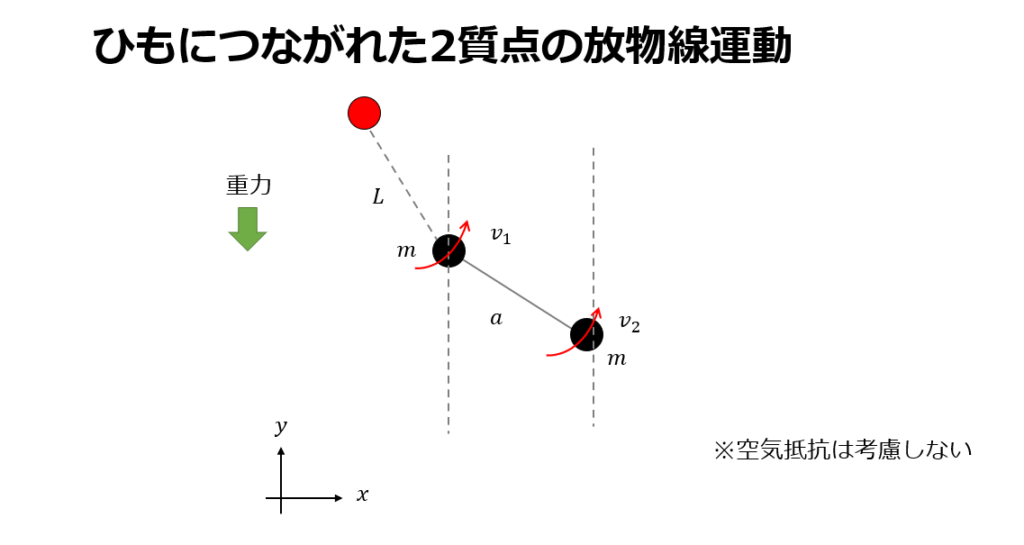
こちらは結局仕事を受けなかったため案件に繋がりませんでしたが、せっかく時間を使ってやったので掲載しておきます。
十分に個人の特定を避けた上で個人で回答した分なので、掲載することに問題はありません。
運動方程式を立てる
2質点の運動を別々で運動方程式を立てるのは面倒なのでここでは簡単に問題を解きたいと思います。
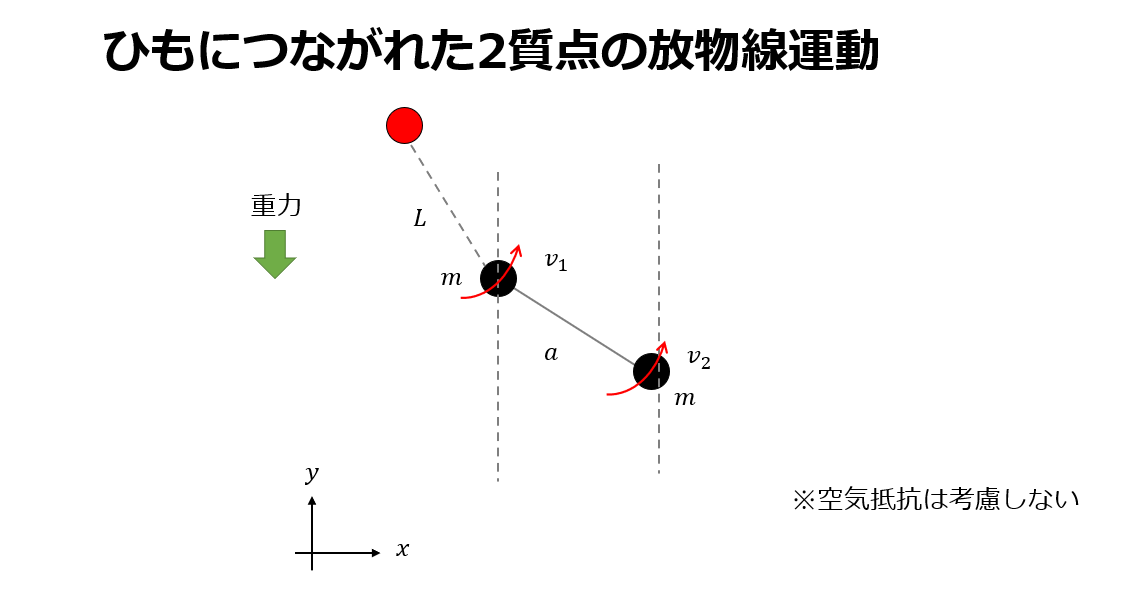
まず、2質点の質量は同じで大きさがないため、重心はひもの中央にあり、重心は放物線を描きながら運動することになります。
以下、問題の解き方の過程を記しまた。
重心の運動が求まったら、質点1と質点2の運動は重心からの相対距離で求まります。
Pythonを使ったシミュレーション
では、Pythonを使ってシミュレーションを行いたいと思います。
Python環境はgoogle colabを使っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
import numpy as np import matplotlib.pyplot as plt from matplotlib import animation, rc from IPython.display import HTML # === time control ==== dt = 0.01 t_final = 1.5 #最終時間 t = np.arange(0, t_final, dt) # === setting parameters ==== g = 9.8 #重力加速度 a = 0.4 # 0.4[m] = 40[cm] 質点1と質点2の距離 # === 質点1 ==== omega1 = 15 # [rad/s] L = 0.2 # 20[cm] 腕の長さ theta1 = 40/180*np.pi # ラジアンに変換 質点1の初期角度 # === 質点1の初速度 === v1x0 = L*omega1*np.sin(theta1) #m/s v1y0 = L*omega1*np.cos(theta1) #m/s # === 質点2 ==== omega = 10 # [rad/s] theta2 = 60.0/180*np.pi # ラジアンに変換 質点2の初期角度 print('重心初期位置(xG, yG)= ', f'{(a/2*np.sin(theta2), -a/2*np.cos(theta2))}') print('重心速度(vGx, vGy)= ', f'{(v1x0+a/2*np.sin(theta2), v1y0+a/2*omega*np.sin(theta2))}') # === 計算開始 === # 重心の位置の計算 xG = a/2*np.sin(theta1) + (v1x0 + a/2*omega*np.cos(theta2) )*t yG = -a/2*np.cos(theta1) + (v1y0 + a/2*omega*np.sin(theta2) )*t - g/2*t**2 # 質点1 x1 = xG - a/2*np.sin(theta2+omega*t) y1 = yG + a/2*np.cos(theta2+omega*t) # 質点2 x2 = xG + a/2*np.sin(theta2+omega*t) y2 = yG - a/2*np.cos(theta2+omega*t) # === 計算終了 ======= # 質点の軌跡の可視化 plt.plot(xG, yG) plt.plot(x1, y1) plt.plot(x2, y2) |
【結果】
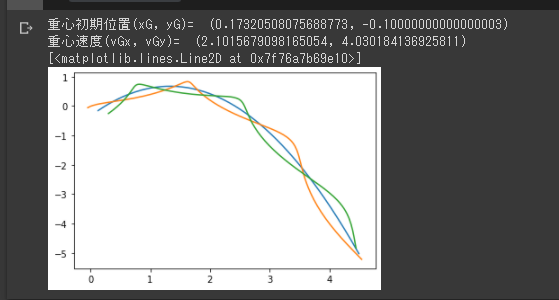
質点1と質点2、重心の軌跡を描きました。
上手くいっていそうな挙動ですね🤗
では、アニメーション作成を行いたいと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#枠線の太さを指定する関数 def axes_set_linewidth(axes, t=1, b=1, r=1, l=1): axes.spines['top'].set_linewidth(t) axes.spines['bottom'].set_linewidth(b) axes.spines['right'].set_linewidth(r) axes.spines['left'].set_linewidth(l) #アニメーション作成 fig, ax = plt.subplots() axes_set_linewidth(ax, t=0, r=0, b=2, l=2) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_xlim(-0.5, 4.0) ax.set_ylim(-0.5, 4.0) ax.legend(frameon = False) plt.subplots_adjust(top=0.9, bottom=0.2, right=0.9, left=0.2) ims = [] #ここに1ステップごとのグラフを格納 for i in range(len(t)): p = ax.plot([x1[i], xG[i], x2[i]], [y1[i], yG[i], y2[i]] , color = 'darkblue', marker = 'o', markersize = 5) ims.append(p) # 質点のどちらかが0より小さくなればアニメーション作成をやめる(メモリ節約のため) # 初期でy<0の場合があるため、0.1より小さい場合とした。 if y2[i] < -0.1 and y1[i] < -0.1: break ani = animation.ArtistAnimation(fig, ims, interval=100) #ArtistAnimationでアニメーションを作成する。 rc('animation', html='jshtml') plt.close() ani |
【結果】
ひもにつながれた2質点の放物線運動 pic.twitter.com/BZDyRjjpT8
— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) December 17, 2021
これで「ひもにつながれた2質点の運動」のシミュレーションを行うことができました。























Great content! Keep up the good work!